パーセントインピーダンス計算法(トランス編)
パーセントインピーダンスの解説はこれで4回目です。
前回ではトランスがある回路の解析手法を記載しましたが、トランスは理想トランスとして扱いました。
今回は、トランスの回路定数を含んだ値で解説を行います。
読者のご高覧を賜れば幸いです。

平成 鹿年 骨月 吉日
貧電工附属 サイタマ・ドズニーランド・大学 学長 鹿の骨
ここで前もってお断りを入れます。
X(エックス)と×(かけ算記号)ですが、非常に紛らわしく、事実上区別して記載出来ません。
従って次の様に書きます。
X(エックス)の場合 :X <==字の下に_を付ける。
×(かけ算記号)の場合:X <==そのまま。
下記はトランスのL型等価回路です。
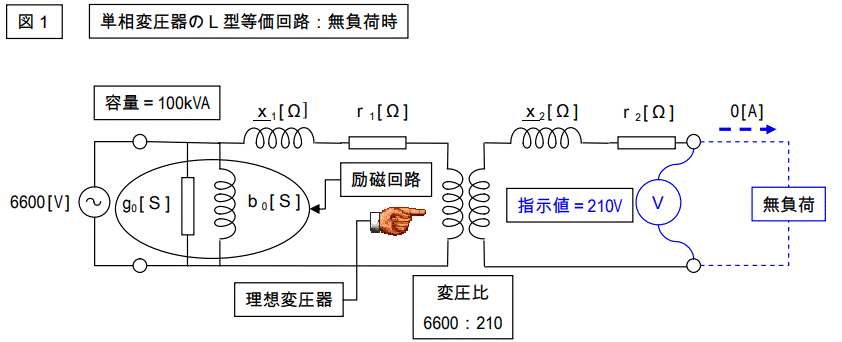
%Zの話云々の前に、定格値の意味するものを正確に理解しておかないと話が頓珍漢になります。
ややこしい話ですが、暫くお付き合い下さい。
まずは、定格値の説明からします。
定格電圧
定格電圧は定格一次電圧と定格二次電圧が有ります。
図1では定格一次電圧=6600[V]、定格二次電圧=210[V]です。
一次側に 6600[V]の交流電圧を加えると二次側に 210[V]の電圧が出現するという意味です。
これには注意が必要で、210[V]がどの様な負荷状態の時の値なのか? を考える必要が有ります。
210[V]は無負荷の状態の値です。
一次側に定格電圧を加え、二次側に負荷を接続し、負荷電流を流した場合は、内部インピーダンスの電圧降下により二次側の端子電圧は下がりますので、二次側端子電圧は定格電圧になりません。
(遅れ負荷の場合。進み負荷を接続した場合は、内部でフェランチ効果が起きて、二次電圧が高くなる事がある。)
二次側端子を開放し、一次側に定格電圧 6600[V]を加えた場合、二次側端子に定格二次電圧 210[V]が出現します。
変圧比
定格一次電圧と定格二次電圧の比率を言います。
通常目にする変圧器は「降圧用の変圧器」です。
電圧の低い方を「1.00」として表すのがお作法のようですので、上記の場合の変圧比は
6600:210=31.4:1.00 となります。(3桁表示)
定格電流
定格電流は定格一次電流と定格二次電流が有ります。
先に定格二次電流が決まります。
実は、定格二次電流は「熱」で決まります。
等価回路で示したように、トランスには発熱の元になる要素が3つ有ります。
一つ目は「鉄損を決める励磁コンダクタンス g0[S]」です。
2つ目は「銅損を決める一次巻線抵抗 r1[Ω]」です。
3つ目は「同じく銅損を決める二次巻線抵抗 r2[Ω]」です。
この3つの内、定格二次電流を決める要素は主に r1 と r2 です。
r1 と r2 は抵抗ですから電流を流すと発熱します。(銅損と言います。)
当然トランスが熱くなりますが、電流を流し過ぎると、熱によって巻線を絶縁している絶縁物が劣化します。
電流を1年2年と連続で流した時に、巻線の絶縁物が「何ともない状態」に保たれる限界の電流があります。
この電流を「定格二次電流」とします。
当然同時に一次電流も流れていますから、一次側でも発熱します。
又、励磁コンダクタンスによる発熱ですが、非常に小さな値ですが確実にあります。(鉄損と言います。)この熱(鉄損)も当然二次側に流れる電流に依る発熱(銅損)同様、定格二次電流の決定に影響します。
この様に定格二次電流は、長い時間ずぅ~っと流していても熱的に問題ない電流を言います。
これが定格二次電流の決め方です。
この定格二次電流以内の電流でトランスを使っている限り、何の問題もありません。
次は定格一次電流です。
この時の、一次電流は定格二次電流を巻数比で割った値になりますが、この値を定格一次電流とします。
此処まで読んできて何も疑問が湧かなかったら、少し勉強不足です。
等価回路にも描きましたが、一次側には励磁回路があります。
二次側に定格電流(負荷電流)を流した場合、一次側に流れる電流は負荷電流と、この励磁電流のベクトル和になります。
一次側に定格電圧を加え、二次側に定格電流が流れる様な負荷を接続した場合、一次側に流れる電流は定格一次電流より大きな値になります。
逆に言えば、一次側の電流を定格一次電流とした場合には、二次側には定格二次電流が流れません。
非常に小さな誤差の範囲ですが、確実に値が異なる事をご理解下さい。
従って、励磁電流と無関係な定格二次電流を先に決める訳です。
定格容量
定格容量は[kVA]の単位を持ちます。
次の計算式で算出された値を言います。
定格容量S[kVA]=定格一次電圧[V]×定格一次電流[A]÷1000=定格二次電圧[V]×定格二次電流[A]÷1000
一次側で計算しても二次側で計算しても計算結果は全く同じです。
ここで注意して頂きたい事は「定格容量」と書いてありますが、「定格出力では無い」という事です。
「容量」と「出力」は違います。
負荷が遅れ負荷の場合、変圧器の二次側には定格容量の負荷を接続できません。
定格容量よりほんの少しですが、小さい負荷を接続する事になります。
例えば 100[kVA]の変圧器に 80[kW]遅れ 80[%](100[kVA]=80[kW]-j60[kvar])の負荷は接続出来ません。
此処は重要なところですから、もう少し詳しく書きます。
前項の等価回路で、R1=9.8596[Ω]、X1=j9.8596[Ω]、R2=0.02[Ω]、X2=j0.03[Ω]だとします。
(数値がヘンなのは、計算をし易いように数値を作ったからが理由。)
この内部インピーダンスを全て二次側に変換すると下記になります。
合計の値をそれぞれR、Xとすると
R=r1/31.42+r2=9.8596/985.96+0.02=0.01+0.02=0.03[Ω]
X=jX1/31.42+jX2=j9.8596/985.96+j0.02=j0.01+j0.03=j0.04[Ω]
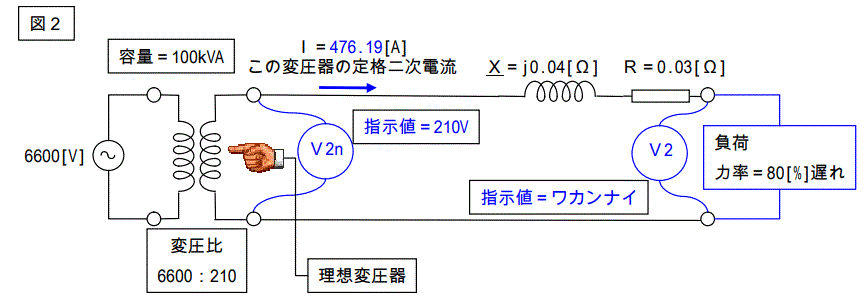
図2の場合の、出力 kVA 値を計算します。(結構厄介な計算です。)
出力 kVA 値は端子電圧×負荷電流で計算できますが、端子電圧V2 が解りません。
電流は絶対値とV2 に対する力率角が解っているだけです。
ちなみにベクトル図を描くと下図になります。V2 を基準としています。
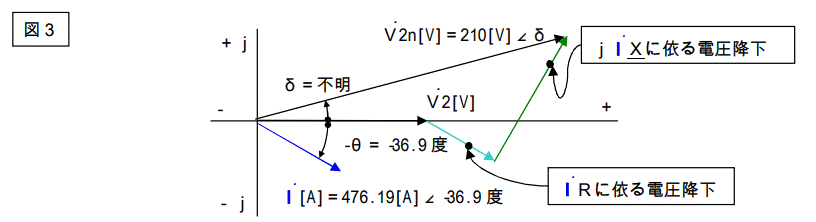
さて計算をスタートしましょう。次のような方程式を立てます。
V2n=I(R+jX)+V2
この方程式に解っている値を代入すると
210[V]∠δ=476.19[A]∠-36.9 度×(0.03[Ω]+j0.04[Ω])+V2∠0
210cosδ+j210sinδ=(476.19×0.8-j476.19×0.6)×(0.03+j0.04)+V2
210cosδ+j210sinδ=11.429+j15.238-j8.571+11.429+V2
210cosδ+j210sinδ=22.858+V2+j6.667
この式の実部と虚部を各々取ると下式を得ます。
210cosδ=22.858+V2・・・ ①式
j210sinδ=j6.667 ・・・②式
②式が先に解けます。
sinδ=6.667/210
δ=1.819310 度 <==関数電卓で計算します。
これを①式に代入すると
210×0.99949=22.858+V2
V2=187.036[V]≒187[V]
V2=187[V]∠0
やっとV2 の値が出ました。
この値に定格電流をかけ算すると、このトランスの力率 0.8 の負荷の場合の出力 kVA 値が出ます。
力率 0.8 の負荷の場合の出力 kVA 値=187[V]×476.19[A]÷1000≒89.0[kVA]
となりますので、容量分の出力は出ない事が解ります。
尚、今回は、トランス内部のインピーダンスを比較的大きな値としています。
実機ではこの様に大きな値では有りません。
概ね 205[V]程度の値になります。(出力≒97.6[kVA]程度)
尚、V2 の値の計算ですが、簡略式を用いて下記のように計算しても算出出来ます。
V2=V2n-I×(Rcosθ+Xsinθ)
=210-476.19×(0.03×0.8+0.04×0.6)
=187.143≒187[V] <==同じ数値と見なせる値が算出される。
電圧変動率
前ページの定格容量の説明で二次側の電圧が負荷の大きさ、力率に依って値が異なる事はご理解されたと思います。
この二次側の電圧の変化を指す指標が「電圧変動率」です。
学術的な定義式は下記です。

V20=指定力率の全負荷時に二次端子電圧が定格二次電圧になるように加えた一次電圧の二次側換算値
指定力率は特に断らない場合は 100[%]とする。
解りますかぁ~?
「ワケガワカラン!」と思うのが普通です。
小生も最初は何を言っているのか全く理解出来ませんでした。
まず、黙って下記の回路図をご覧下さい。
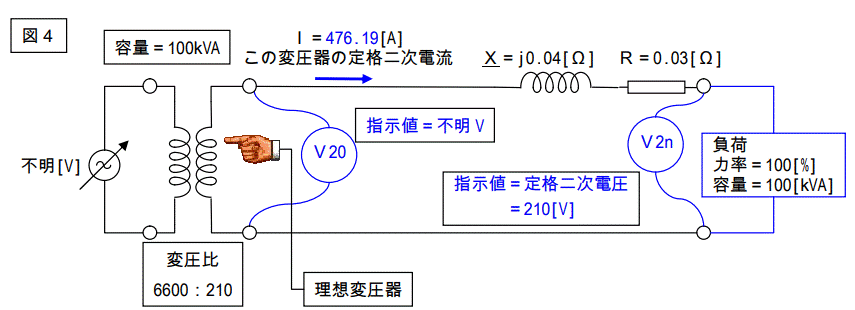
「図2と同じジャン・・・」ではありません。
図4をヨーク見ると解りますが、二次端子電圧が定格二次電圧になっています。
トランス内部で電圧降下を起こしますから、当然一次側の端子に加える電圧は定格一次電圧ではありません。
定格一次電圧より高い電圧を加えないと二次端子電圧が定格電圧になりません。
この回路図のベクトル図を描くと図5になります。
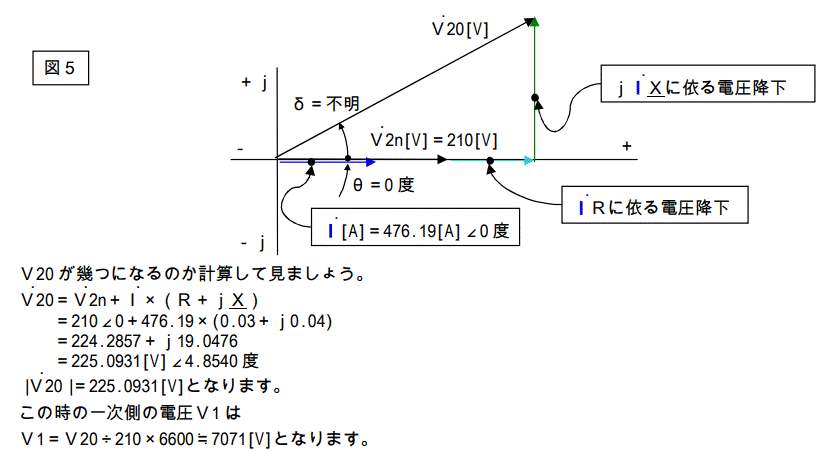
今度は下記の回路図をご覧下さい。
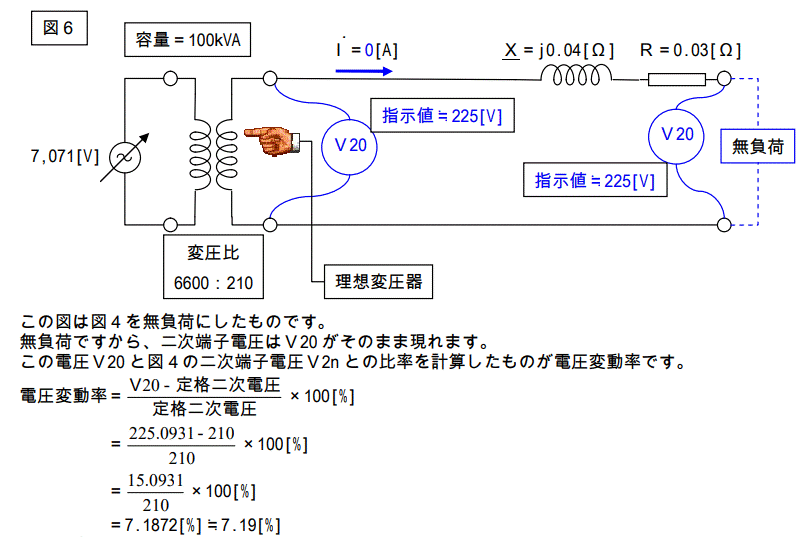
となります。
ここで注意したい事は、電圧変動率は「どの位電圧が下がるか。」と言う指標ではありません。
「電圧がどの位上がるか。」と言う指標です。
この計算は負荷の力率が 100[%]の場合で計算しました。
力率が変わったらどうなるでしょうか? 実は電圧変動率の値も変わります。
下記に計算のみを記載します。
力率=80[%]の時のV20 が幾つになるのか計算して見ましょう。
V20=V2n+I×(R+jX)
=210∠0+476.19∠-36.9×(0.03+j0.04)
=210∠0+476.19×(0.8-j0.6)×(0.03+j0.04)
=210∠0+476.19×(0.024+j0.032-j0.018+0.024)
=210∠0+476.19×(0.048+j0.014)
=210∠0+22.85712+j6.66666
=232.85712+j6.66666
=232.95253∠1.6399 度
|V20|=232.95253[V]となりますので、力率 100[%]の時と値が異なります。
この時の電圧変動率は

となります。
従って、電圧変動率を定義する時は「力率」の値を同時に定義しておかないと、計算できません。
効率

無効電力(遅相無効電力又は進相無効電力)は無関係です。
トランスの効率を計算する時は、負荷力率を 100[%]として計算します。
これは力率が 100[%]で無い場合を計算すると、このトランスの効率の定義が出来ないからです。
例えば極端な例として、力率 0.00[%]のリアクトルを接続した場合、出力=0.00[kW]ですから、このトランスの効率は 0.00[%]になってしまいます。
これでは案配が悪い事になります。ですから 100[%]力率の負荷の場合で計算します。
実際に計算をやって見ましょう。
下図の場合で計算します。
一次側に定格一次電圧(6600[V])を加え、二次側の電流が定格二次電流になるようにしたした回路です。
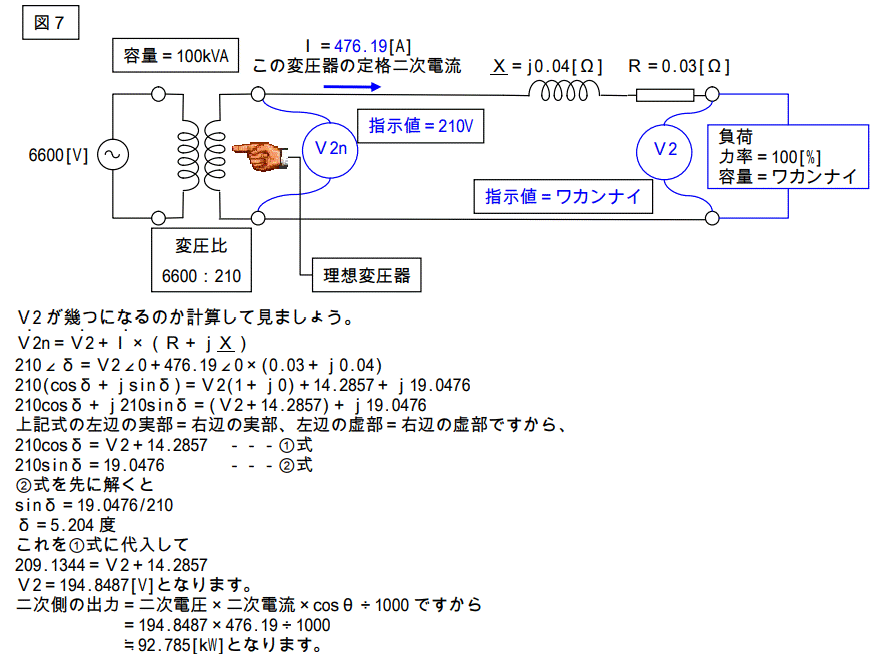
入力の値を計算するために、トランス内部の損失を計算します。
銅損から計算します。
銅損=導体抵抗×電流×電流÷1000
=0.03×476.19×476.19÷1000
≒6.803[kW]
鉄損の値を計算します。
図1の励磁回路部分で消費される有効電力の値です。
励磁コンダクタンスの値が示されていませんので、二次側換算の g0=0.01[S]とします。
鉄損=励磁コンダクタンス×電圧×電圧÷1000
=0.01×210×210÷1000
=0.441[kW]
入力=出力+銅損+鉄損ですから
=92.785[kW]+6.803[kW]+0.441[kW]
=100.029[kW]
従って効率は

なにやら普通の計算を行っているように見えますが、ヨーク見るとかなりヘンな計算を行っています。
出力に当たる部分の計算が、V2n×I2n×cosθと書いてありますが、これをそのまま書き直すと、定格二次電圧×定格二次電流×負荷力率となります。
「出力の計算に定格二次電圧を使っている。」これってオカシイじゃないか!と思ったあなたは賢い!
この計算は実際の二次端子電圧とは無関係に、二次端子電圧は常に定格二次電圧で一定として計算しています。
この様な計算手法を用いると、負荷電流の計算が非常に楽になります。
二次端子電圧がワカンナイという事は無くなる事になりますから負荷電流の計算は楽です。
又、鉄損の計算は「定格鉄損」で計算すると言っています。
つまり、定格鉄損が計上される一次電圧は、定格一次電圧ですが、この時の二次端子電圧は当然定格二次電圧では有りません。
にも関わらず、二次端子電圧が定格二次電圧になっているとして計算すると言う事です。
速い話、インチキ計算ですが、実機の場合、内部電圧降下は非常に小さい値ですので、このインチキ計算で充分実用になります。
従って、世の中で特に断らない限り、トランスの場合の効率はこの規約効率を指します。
上記の規約効率の式は二次電流が定格電流の場合の式ですが、負荷が 100[%]負荷で無い場合は下記の式になります。
nを負荷率として、
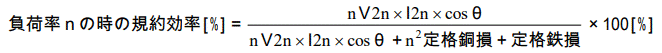
%Z、%R、%Xの値
やっとパーセントインピーダンスの話です。
ここで問題を出しますので考えて下さい。
問題
下図の3つの場合のIR、IX、IZの値を計算しなさい。
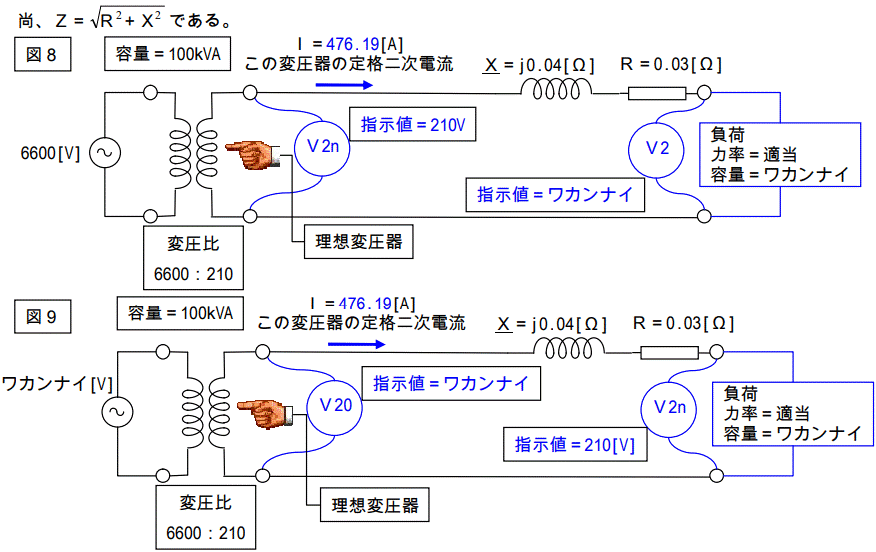
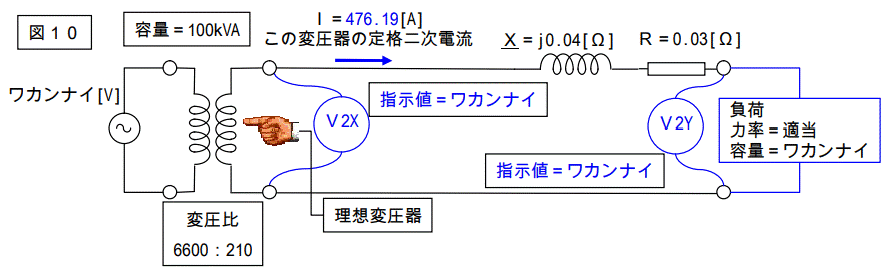
もの凄く変な問題です。
図8は一次電圧が定格一次電圧の場合、図9は二次端子電圧が定格二次電圧の場合、図10はいずれでも無い場合です。
いずれの場合も負荷力率は定義されていませんし、容量も不明です。
一つだけ確実に解っている事は、「二次電流が定格二次電流」という事です。
これで、「IR、IX、IZの値を計算しなさい。」と言っています。
ですから、計算は恐ろしく簡単で、三図とも共通で下記の計算式になります。
IR=476.19[A]×0.03[Ω]=14.2857[V]
IX=476.19[A]×0.04[Ω]=19.0476[V]
IZ=476.19[A]×0.05[Ω]=23.8095[V]
これで計算は終わりです。
ところで何のためにこんな計算をしたのかは次に示します。
続いて、又変な計算を行います。
次にに示す式の値を計算をして下さい。(%値で示して下さい。)
I2nR/V2n の値、I2nX/V2n の値、I2nZ/V2n の値 (V2n は定格二次電圧、I2n は定格二次電流です。)
I2nR/V2n=14.2857[V]/210[V]×100[%]=6.802714286[%] ---①の値
I2nX/V2n=19.0476[V]/210[V]×100[%]=9.070285714[%]---②の値
I2nZ/V2n=23.8095[V]/210[V]×100[%]=11.33785714[%]---③の値
実はこの値は各々パーセントインピーダンスの値です。
①の値=%Rの値
②の値=%Xの値
③の値=%Zの値 です。
パーセントインピーダンスの値だという事は、この値を用いて短絡電流の計算が出来るはずです。
やってみましょう。
短絡電流=基準電流÷%Z×100
=定格二次電流÷%Z×100
=476.19[A]÷11.33785714[%]×100
=4200[A]
オームインピーダンス法で計算すると
インピーダンス=0.03+j0.04=0.05[Ω]∠53.9
短絡電流=定格二次電圧÷インピーダンス(一次側に定格電圧を加え、二次端子間を短絡した場合。)
=210÷0.05
=4200[A]
となりますので、全く同じ結果となります。
ここで、次の計算をして下さい。
パーセントインピーダンスの値を用いて、このトランスの電圧変動率を計算して下さい。
電圧変動率の値は%値で示されますし、%Zの値も%値で示されます。
だったら、この数字をコネクリマワすと電圧変動率の計算も出来るのではないのか?と考えます。
実際に出来ます!!計算結果を先に示します。

この計算結果と、前項で行った計算結果を比較すると同じ値が算出されている事が解ります。
つまりこの計算は・・・・合っている! しかし・・・これは何の計算をやったのだ??
ベクトル図を書いて見ると理解が早いかも知れません。
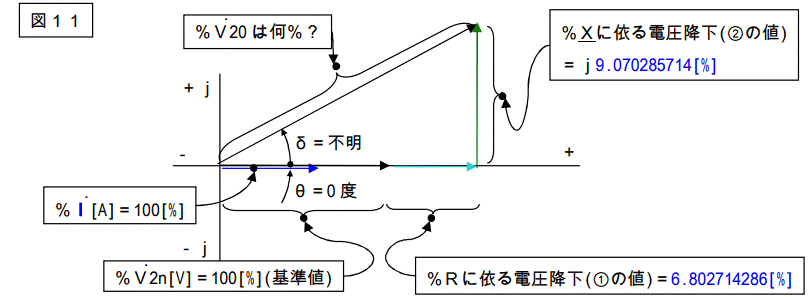
これは図5を%の値で書いたベクトル図です。図5と併せてご覧下さい。
この様に%の値でもベクトル図は描けます。
何の事は無い。ピタゴラスの定理を用いてV20 の長さを計算しているだけです。
Iは定義により負荷力率が 100[%]ですからIRはIと同相になります。
IXは 90 位相を持ちます。
続いて、負荷力率が 80[%]の時の電圧変動率を計算します。
計算は終わっていますが、≒10.93[%]になるはずです。
ベクトル図を描くと下図になります。ちなみに電流値は定義に従い定格値です。
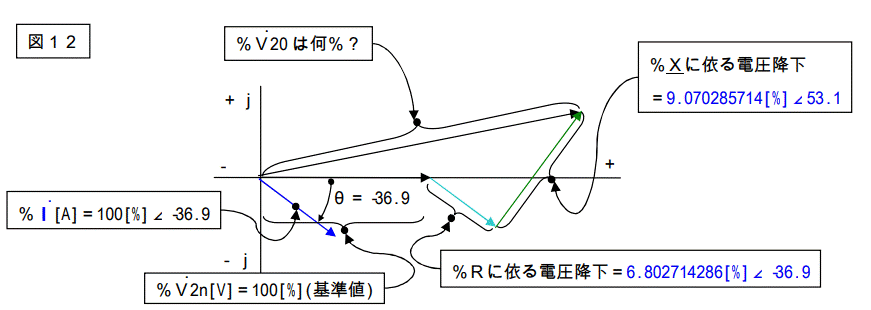
図12のベクトル図に記載された%R及び%Xの%値表示が図11と少し違います。
「∠」が付いています。図11の場合も「∠」が実は有るのですが、0度と90度でしたのであまり注意深く書きませんでした。
今度は微妙な値を取りますので、正確に書いています。
早速%V20 をベクトル演算で求めます。下記の式が成立します。

続いて、再度負荷力率が 100[%]及び 80[%]の時の電圧変動率を計算します。
今度は条件を変えて、一次側に加えた電圧が定格一次電圧の場合です。
計算が面倒臭いので簡便式を使って良い事にします。
下記に示すような%ベクトル図が描けます。
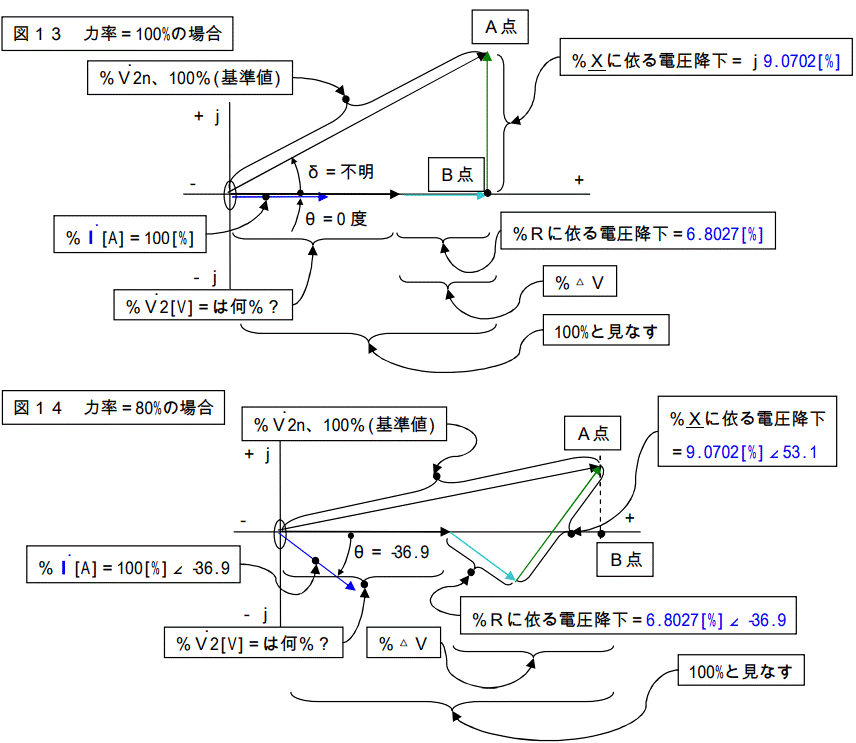
簡便式を使って計算すると言う事は、上記2図に於いて、O~Aの長さをO~Bの長さとして計算すると言う事です。
図では異なる長さに見えますが、実際はδがさほど開いてはいませんので、この計算でも誤差は少なくなります。
では計算して見ましょう。
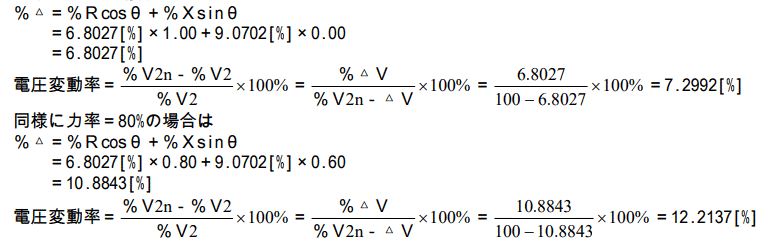
これらの事から次項に示す事が解ります。
力率=100%の場合に於いて、二次電流が定格電流で、一次側に定格電圧を加えた場合
二次端子電圧=定格電圧×%二次端子電圧
=定格電圧×(100%-%△V)
=210[V]×(100[%]-7.2992[%])
=210[V]×92.701[%]=194.6721[V]
出力 KVA 値=定格容量×%出力 KVA 値
=定格容量×%二次端子電圧×%二次電流
=定格容量×(100[%]-%△V)×100[%]
=100[kVA]×(100[%]-7.2992[%])×100[%]
=100[kVA]×92.701[%]=92.701kVA
力率=80%の場合に於いて、二次電流が定格電流で、一次側に定格電圧を加えた場合
二次端子電圧=定格電圧×%二次端子電圧
=定格電圧×(100[%]-%△V)
=210[V]×(100[%]-12.2137[%])
=210[V]×87.7863[%]=184.3512[V]
出力 KVA 値=定格容量×%出力 KVA 値
=定格容量×%二次端子電圧×%二次電流
=定格容量×(100%-%△V)×100[%]
=100[kVA]×(100[%]-12.2137[%])×100[%]
=100[kVA]×87.7863[%]=87.7863kVA
前項で力率=80%の時の出力 kVA の値を計算しましたが、結果は 89[kVA]でした。
今回の計算結果が≒88[kVA]ですから、計算結果は事実上同じと見なせます。
この様に、トランスの内部インピーダンスをパーセントインピーダンスの値で示し、これを使って色々な計算が出来ることが解ります。
実際には%の値で示された方が計算は楽になります。
例を示します。
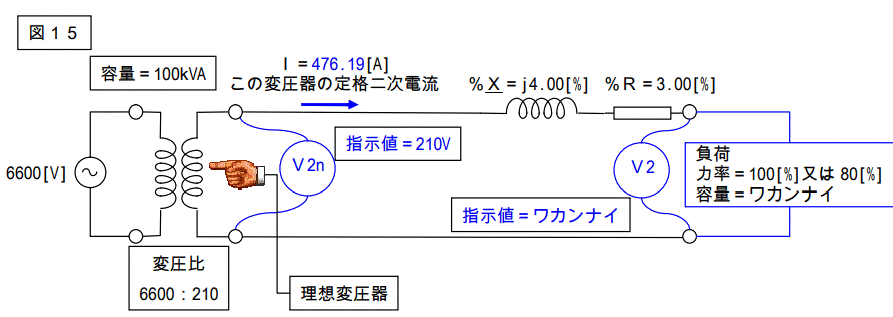
この図はインピーダンスを%値で示したものです。
V2 値を計算してみましょう。
力率=100%の場合
%△V=%Rcosθ+%Xsinθ=3.00[%]×1.00+4.00[%]×0.00=3.00[%]
%V2=%V2n-%△V=100[%]-3.00[%]=97.00[%]
したがってV2=定格二次電圧×%V2=210[V]×97.00[%]=203.70[V]
力率=80[%]の場合
%△V=%Rcosθ+%Xsinθ=3.00[%]×0.80+4.00[%]×0.60=4.80[%]
%V2=%V2n-%△V=100[%]-4.80[%]=95.20[%]
したがってV2=定格二次電圧×%V2=210[V]×95.20[%]=199.92[V]
電圧変動率(定義式に基づいたもの)を計算してみましょう。
力率 100%の場合・・・上のV2 の計算途中で計算は出来ていますから改めて計算するまでもありません。
%△V=電圧変動率=3.00[%]
力率=80[%]の時は 4.80[%]です。
この図15の電圧変動率を計算してみましょう。
力率=100[%]の場合
この図の電圧変動率={(%V2n-%V2)/%V2}×100[%]
={(100-97.00)/97.00}×100[%]=3.0928[%]
同様に力率=80%の時は
この図の電圧変動率={(100-95.20)/95.20}×100[%]=5.0420[%]
となります。
この時の出力 kVA 値を計算してみましょう。
力率 100%の時
%出力 kVA 値=%出力電流×%出力電圧
=100[%]×97[%]=97[%]
出力 kVA 値=基準容量×%出力 kVA 値
=100[kVA]×97[%]=97[kVA]
力率 80%の時
%出力 kVA 値=%出力電流×%出力電圧
=100[%]×97[%]=95.20[%]
出力 kVA 値=基準容量×%出力 kVA 値
=100[kVA]×95.20[%]=95.20[kVA]
となります。
この様に、内部インピーダンスが%値で示された場合は色々な計算が、単に比率を取るだけで終わります。
つまり計算が楽な訳です。
ですから、一般的に変圧器の特性は%値で示される事が多いようです。
最後にこのトランスをインピーダンスの有る配線に接続した場合の事を書きます。
何の事は無い!全部足し算してハイオシマイ!チャンチャン・・・。
コレジャあんまりなんで、もう少し書きます。
問題
下記の□□電流と○○電流を求めなさい。
尚、各パーセントインピーダンス値は基準容量が 100[kVA]の時の値である。
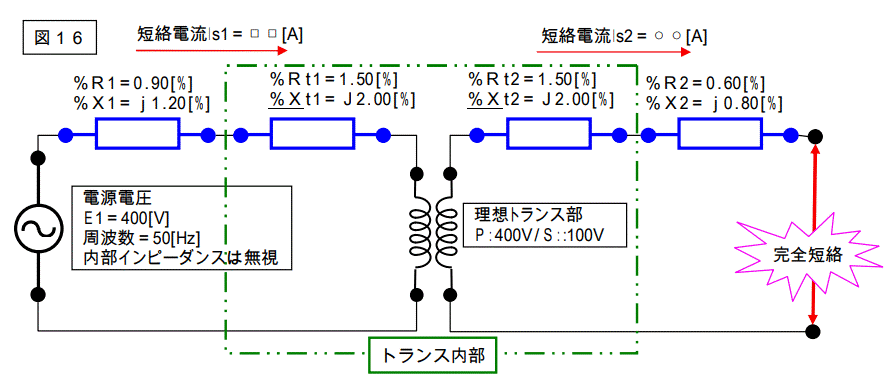
この回路のパーセントインピーダンスを全部足し算します。
Σ%R=0.90+1.50+1.50+0.60=4.50[%]
Σ%X=j1.20+j2.00+j2.00+j0.80=j6.00[%]
Σ%Z=√(Σ%R2+Σ%X2)=√(4.50[%]2+6.00[%]2)=7.5[%]
○○電流=100V の基準電流÷Σ%Z=100000[VA]÷100[V]÷7.5[%]=13,333[A]
□□電流=400V の基準電流÷Σ%Z=100000[VA]÷400[V]÷7.5[%]=3,333[A]
これでオシマイ!あっけなく計算は終わります。
まとめと pu 法について
今回は盛りだくさんで色々書きましたが、少し整理します。
オームインピーダンスを使った計算を「直接計算法」とすると、パーセントインピーダンスを使った計算は「間接計算法」という事が出来ると思います。
パーセントインピーダンス法は名前の通り、%で表した比率を用いた計算法です。
ですから、原理を理解していないと、完全に訳が解らない計算になります。
パーセントインピーダンスを用いて、電圧変動率の計算が出来る事は、直感的にご理解願えると思いますが、「%二次端子電圧」「%出力 kVA 値」などは、ナンジャコリャと思われたと推測します。
流れる電流を「定格電流=100[%]」と定義して計算をスタートしていますので、この様な%値も定義することが出来ます。
此処いら辺は、慣れないと何ともし難い所ですが、何回か練習しているとその内、勘が働く様になります。是非習得して、慣れて下さい。
ここで、「pu 法」に関して書いておきます。
「pu」は「パーユニット」と読みます。
パーセントインピーダンス法と pu 法は全く同じものですが、値が 100 倍異なります。
例えば、「3」という数値を「100を基準」で表すと
「3は100の 3.00[%]である。」と書いたら、これはパーセントインピーダンス法の表現方法です。
「3は100の 0.03[pu]である。」と書いたら、これは pu 法の表現方法です。
速い話、%値で書くか、小数で書くかの違いです。
%を用いて比率を表すと、数値が落ち着きますので何かと都合が良いのですが、計算途中に「100倍」又は「100分の1」が出てきます。
これを間違えると、計算結果が100倍狂ったり、挙げ句の果てに10000倍狂ったりします。
どうも案配が良くないなぁ~・・・と言う事で、pu 法を用いるとこの様なミスを防ぐ事が出来ます。
昔と違い、今はコンピュータで計算が簡単に出来ますので、pu 法の方が実情に合う様な気がします。
慣れて来ると pu 法の方が計算が楽です。
例題を示しますので考えて下さい。(この問題は難しいです。ハイ!)
問題
下記は、6%リアクトル付き普通高圧コンデンサ、設備容量 100[kvar]の回路図である。
下記?の値が幾つになるか計算しなさい。
図中※1及び※2の解説は次ページ参照。
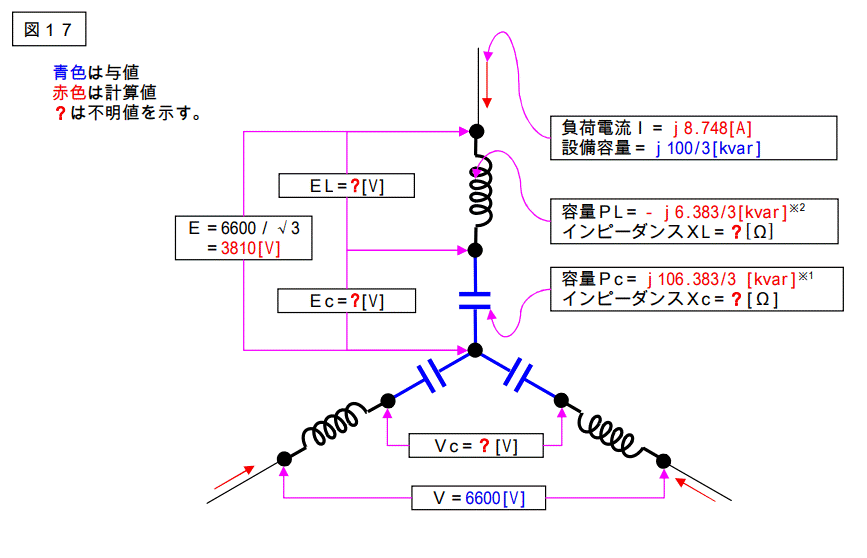
※1 及び※2 の解説
設備容量 100[kvar]、6[%]リアクトルの場合で説明します。
設備容量が先に決められますので、100[kvar]の場合では、6[kvar]のリアクトルと 106[kvar]のコンデンサを直列に接続すれば良いように思えます。
実際、設備容量の6%の容量を持つリアクトルと、設備容量の106%の容量を持つコンデンサを直列に接続すれば、次式が成立します。
設備容量=-j6[kvar]+j106[kvar]
=j100[kvar]
これで何の不都合も無いと思われますが、JIS の規定はこの様な容量の決め方をしていません。
JIS の容量の決め方は下記です。
6[%]の場合
コンデンサ容量=設備容量/(1-6%/100)
=設備容量の 1.063829787 倍
リアクトル容量=コンデンサ容量の 6%
=設備容量の 1.063829787 倍の 0.06 倍
=設備容量の 0.063829787 倍
コンデンサ容量-リアクトル容量=設備容量の 1.00 倍丁度
この様にへんてこりんな容量の決め方をしているのは、リアクトルのインピーダンス値とコンデンサのインピーダンス値の比率が 6.00%丁度になるようにするためです。
|コンデンサのインピーダンス|:|リアクトルのインピーダンス|=1:0.06
となります。
6[kvar]のリアクトルと 106[kvar]のコンデンサではインピーダンスの比率が 6.00[%]丁度になりません。ご注意下さい。
さて、この問題を pu 法で解きます。
基準容量を 100/3[kVA]≒33.3333[kVA]=1.00[pu]とし、基準電圧を 6600/√3[V]≒3810.5[V]=1.00[pu]とします。
基準電流は 100/3[kVA]÷6600/√3[V]≒8.7477[A]=1.00[pu]です。
基準インピーダンスは基準電圧の時に基準電流を流す大きさになりますから、
基準インピーダンス=6600/√3[V]÷8.7477[A]≒435.60[Ω]=1.00[pu] となります。
1相分のリアクトル容量を pu 値で示すと、-j6.383/3[kvar]÷100/3[kVA]=-j0.06383[pu]となります。
同様に1相分のコンデンサ容量はj1.06383[pu]です。
これらの値を用いて図17を書き直すと下図になります。
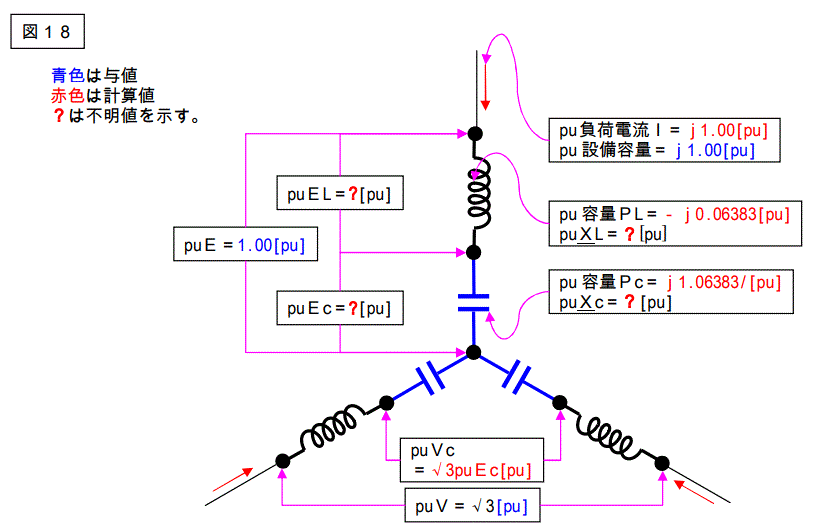

pu値が出そろいましたので、元の値に換算します。
XL[Ω]=基準値[Ω]×puXL[pu]
=435.60[Ω]×j0.06383[pu]
=j27.8043[Ω]
EL[V]=基準値[V]×puEL[pu]
=6600/√3[V]×-0.06383[pu]
=243.22497[V]
Xc[Ω]=基準値[Ω]×puXc[pu]
=435.60[Ω]×-j1.06383[pu]
=-j463.4043[Ω]
Ec[V]=基準値[V]×puEc[pu]
=6600/√3[V]×1.06383[pu]
=4053.7367[V]
Vc[V]=基準値[V]×puVc[pu]
=6600/√3[V]×1.84261[pu]
=7021.28711[V]
これで計算は終わりです。
Vc[V]の値が≒7,021[V]となりますので、加えた電圧の線間電圧6600[V]より高い電圧になります。
これは、リアクタンスの電圧降下が、フェランチ効果により電圧上昇となっているためです。
ワカッタかなぁ~・・・??
多分・・・ワケガワカラン×100倍!!・・・だと思います。
pu法の計算は、何回か練習している内に自然と身に付きます。
初めは何が何だか全く解りませんが、その内解るようになります。
ですから、安心して悩んで下さい。
事項に、この問題をオームインピーダンス法で解いたものを示します。
両者を見比べて違いなどを把握して下さい。
オームインピーダンス法で解いた場合
S=|I|2・Z(バー)

となりますので、pu法で計算した結果と同じ結果になります。
どちらの計算が「樂」かは各自で判断して下さい。
本日の講義はこれで終わりです。
多分、アタマの中がグルングルンになっていると思います。
一度読んで解らなかったら、二度読んで下さい。
三回読んで解らなかったら、もう読むのを止めて下さい。
後何回読んでも無駄です。他の参考書をお読み下さい。
次ページは補習です。
補習 電力を求める式の色々。
電力を求める式は色々あります。
基本式は下記です。
電力S[W及びvar]=電圧E(バー)[V]×電流I[A] <==公式です。
例を示します。
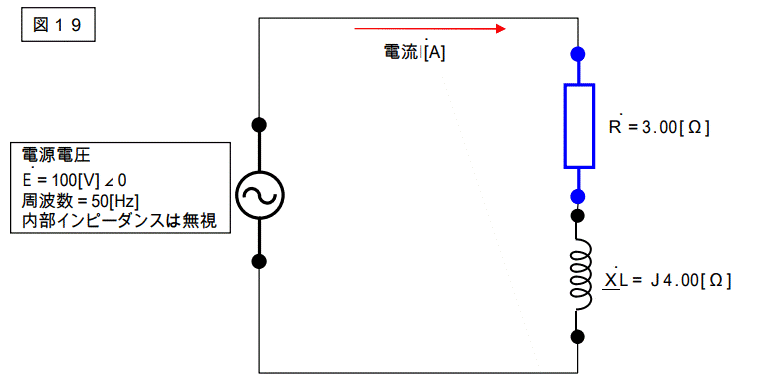
この回路のインピーダンスを求めます。
Z=R+XL
=3.00[Ω]+J4.00[Ω]=5.00[Ω]∠36.9
電流Iは
電流I=電源電圧(ドット)÷インピーダンス(ドット)
=100[V]∠0÷5.00[Ω]∠36.9=20[A]∠-36.9
この回路の有効電力は
P=電圧×電流×cosθ <==スカラー式です。
=100[V]×20[A]×cos-36.9=100[V]×20[A]×0.80=1600[W]
この回路の無効電力は
Q=電圧×電流×sinθ <==スカラー式です。
=100[V]×20[A]×sin-36.9=100[V]×20[A]×-0.60=-1200[var](負値で示されるので、遅れです。)
基本式で求めると

となりますので同じ結果になります。
この式をバラバラに計算すると

となりますのでやはり同じ結果になります。
又、別の式を考えます。
基本式を変形します。

となりますのでやはり同じ結果になります。
まとめ
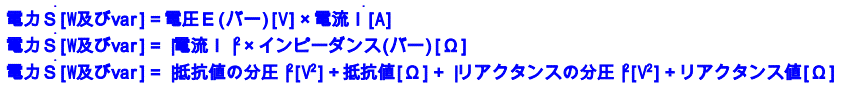
以上の3つの式で電力の計算が出来ます。
【オシマイ】





















































コメント