パーセントインピーダンスとは何か・・・ではない始まり方です。いつの間にかパーセントインピーダンスで短絡電流を計算していく解説手法です。いつの間にかパーセントインピーダンス法で計算ができるかも。
パーセントインピーダンス計算法入門
電気屋をやっていると、短絡電流の計算を行う羽目になる事がよくあります。
この時パーセントインピーダンスを使って計算すると、計算が楽です。
しかし、この計算手法は解ってしまうと非常に便利な計算方法なのですが、解らないと、トコトン解らない手法です。市中には、色々な解説書が有りますが、難解で読んでいる内にワケガワカランという事になってしまうものも有ります。
ここでは、出来るだけ解りやすい様に解説を書きました。
読者のご高覧を賜れば幸いです。

平成 鹿年 骨月 吉日
貧電工附属 サイタマ・ドズニーランド・大学 学長 鹿の骨
で・・・、いきなり問題を出します。
【問題1】
下記回路で短絡事故が発生しました。
短絡電流の大きさ求めなさい。
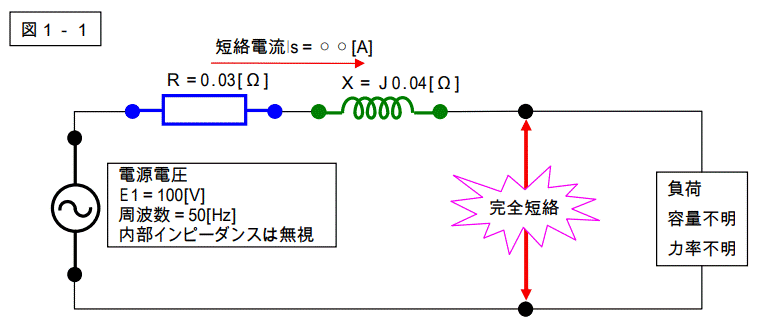
【解答1】
一見難しそうに見える問題ですが、実はもの凄く簡単です。
負荷の容量及び力率は不明ですが、短絡点が負荷の電源側ですから、負荷の容量は計算に関係あり
ません。
又、電源の周波数も計算に無関係です。(ただ書いてあるだけ。)
従って、下記の回路の計算を行えば良いことになります。
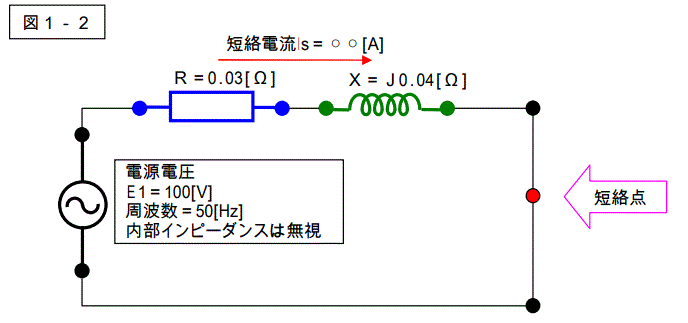

別に難しい問題でも何でもありません。初等交流回路計算のまんまです。
こんどは、次の問題を解いて下さい。
【問題2】
下記の様な回路があります。
この回路に於いて、各電圧計で計測される電圧値、及びベクトル図を描いて下さい。
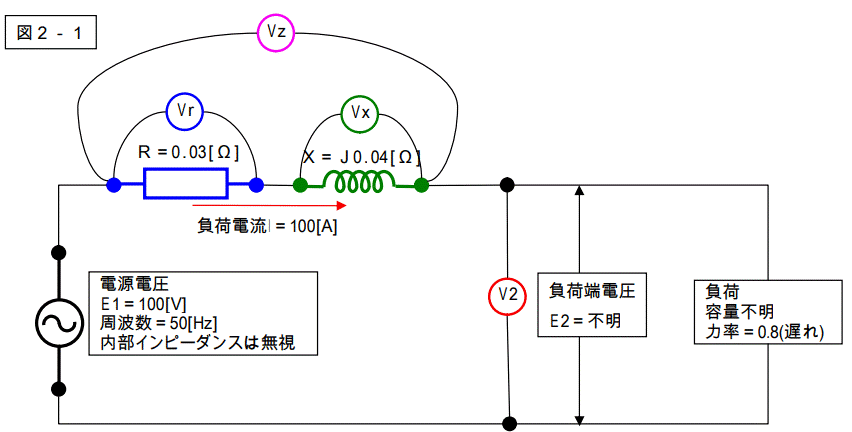
【解答2】
この問題、難しいです。ハイ。(電験三種のB問題程度か?)
下記にベクトル図を示しますので、これを見ながら解法を考えましょう。

このベクトル図に電源電圧のベクトルと、配線の電圧降下のベクトルを加筆すると下図になります。
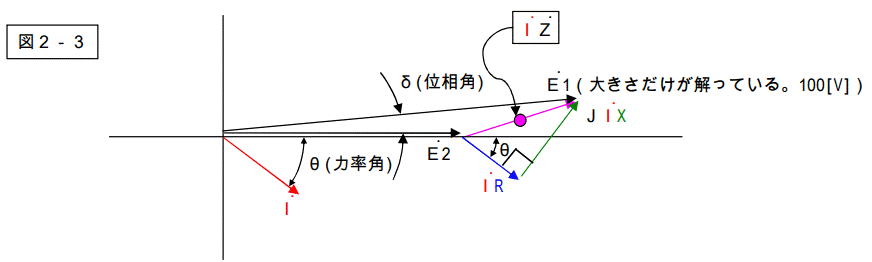
この図から解る通り、E1 は下記の式で表す事が出来ます。
E1=E2+IR+JIX
これに各値を代入すると下記になります。
100(COSδ+JSINδ)=E2+(80-J60)×0.03+(80-J60)×J0.04
100COSδ+J100SINδ=E2+2.4-J1.8+J3.2+2.4
100COSδ+J100SINδ=(E2+4.8)+J1.4
上記の式は複素数の式ですから下記の関係式が成立します。
左辺の実数部=右辺の実数部
左辺の虚数部=右辺の虚数部
従って下記の関係式が成立します。
100COSδ=E2+4.8(実数部)--- ①式
100SINδ=1.4(虚数部) ----- ②式
②式が先に解けます。(関数電卓を使います。)
SINδ=0.014
δ=0.802 度
従って COSδ=0.9999(COSδ=√(1-SIN2δ)として解いても同じ。)
これを①式に代入して
100COSδ=E2+4.8
99.99=E2+4.8
E2=95.19[V]となります。
これで全部の値が解りました。
整理すると次の様になります。
基準ベクトルはE2 とします。(E2=E2∠0 度です。)
δ=0.802 度
θ=-36.9 度
E1=100∠0.802 度[V]=99.99[V]+J1.4[V]
E2=95.19∠0 度[V]=95.19[V]+J0[V]
I=100∠-36.9 度[A]=80[A]-J60[A]
IR=I・R=100∠-36.9 度[A]×0.03[Ω]=3∠-36.9 度[V]=2.4[V]-J1.8[V]
IX=I・JX=100∠-36.9 度[A]×0.04∠90 度[Ω]=4∠53.1 度[V]=2.4[V]+J3.2[V]
IZ=I・Z=100∠-36.9 度[A]×0.05∠53.1 度[Ω]=5∠16.2 度[V]=4.8+J1.4
となります。
ついでに計算すると
負荷皮相電力=|E2|・|I|=95.19[V]×100[A]=9.519[kVA]
負荷有効電力=皮相電力×力率=9.519[kVA]×0.8=7.615[kW]
電圧降下は概ね5%であることも解ります。
引き続き下記の問題を解いて下さい。
【問題3】
問2で算出した値の内、下記の比率を計算しなさい。(%値で答えなさい。)
① |IR|/|E1|
② |IX|/|E1|
③ |IZ|/|E1|
【解答3】
これ、もの凄く簡単です。アホみたいな問題です。
① |IR|/|E1|=3[V]÷100[V]×100[%]=3[%]
② |IX|/|E1|=4[V]÷100[V]×100[%]=4[%]
③ |IZ|/|E1|=5[V]÷100[V]×100[%]=5[%]
ところでこんな計算をやらして何考えてるの?
いいから次へ進め!
引き続き下記の計算を行い、算出結果を考察しなさい。
【問題4】
問題2の電流値を問題3で算出した値の③の値で割りなさい。
【解答4】
問2の電流値は 100[A]。
問3で算出した値の③の値は 5[%]
電流値を%値で割れと言っているので
100[A]÷5[%]=2000[A]となります。
オイ!!チョット待て! この数字見覚えがあるぞ!!
そうです。この電流は短絡電流です。
何故この様な計算を行うと短絡電流が求まるのかを説明します。
下記に2つのベクトル図を描きます。
1つは問題1のベクトル図、もう一つは問題2のベクトル図です。
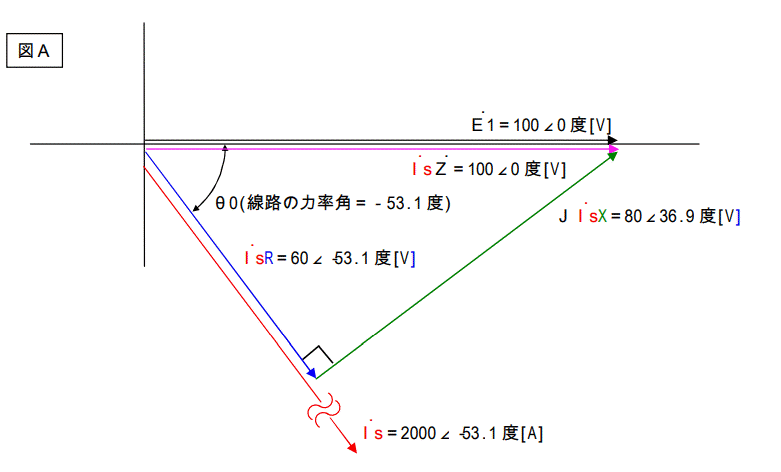
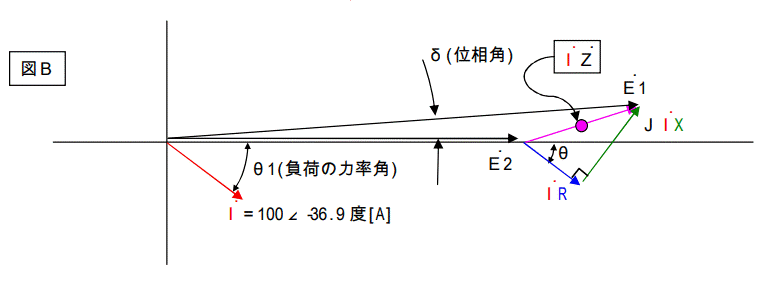
この二つのベクトル図をよく見るとあることに気が付きます。
電圧降下を表す二つの三角形に注目して下さい。
もう一度図を掲載します。(一部省略)
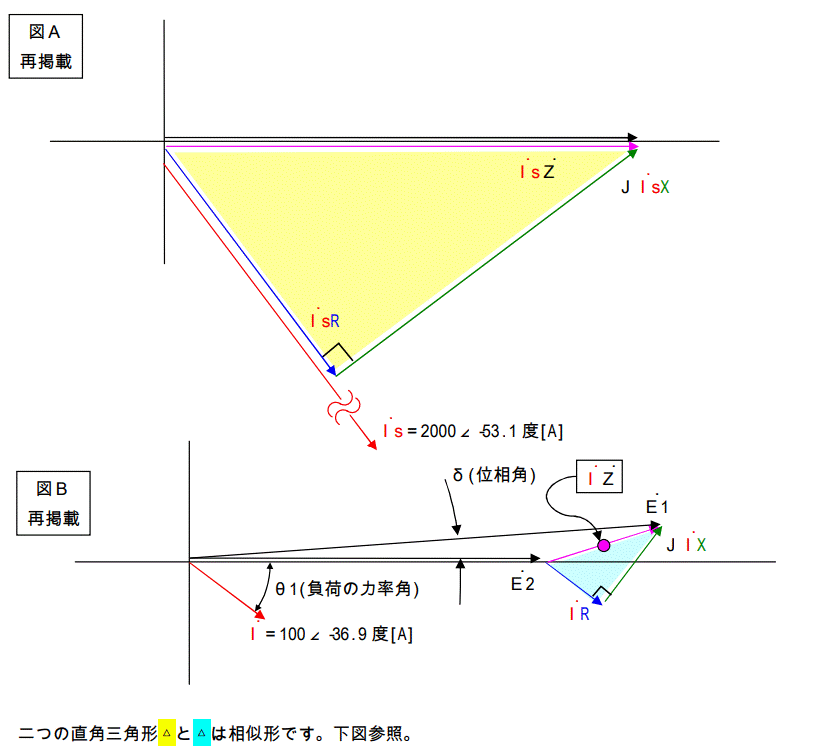
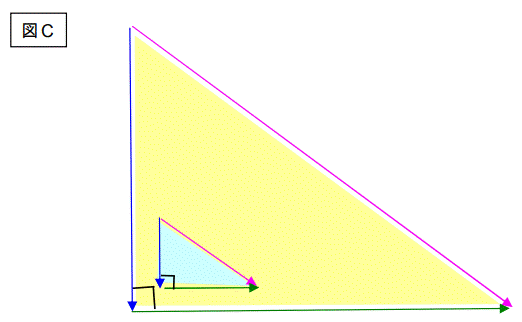
ですから、電圧降下の値と電源電圧の値の比で、負荷電流値を割ると、短絡電流値が算出、出来ます。
ウゥ~ン??解ったような解らないような感じです。
図Bは負荷の力率を考慮したベクトル図です。
図Aは負荷の力率に関係ないベクトル図です。
負荷の力率は何処に行っちゃうの?と言う疑問も湧きます。
理解を確実にするために次の問題を解いて下さい。
【問題4】
下記の回路で、負荷力率が変化した場合のベクトル図を描きなさい。(問題2と回路図は同じ。)
負荷力率は次の値とします。
①.COSθ=0(進み)
②.COSθ=1
③.COSθ=0.8(遅れ)
④.COSθ=0.6(遅れ)
⑤.COSθ=0(遅れ)
負荷電流は 100[A]で一定です。
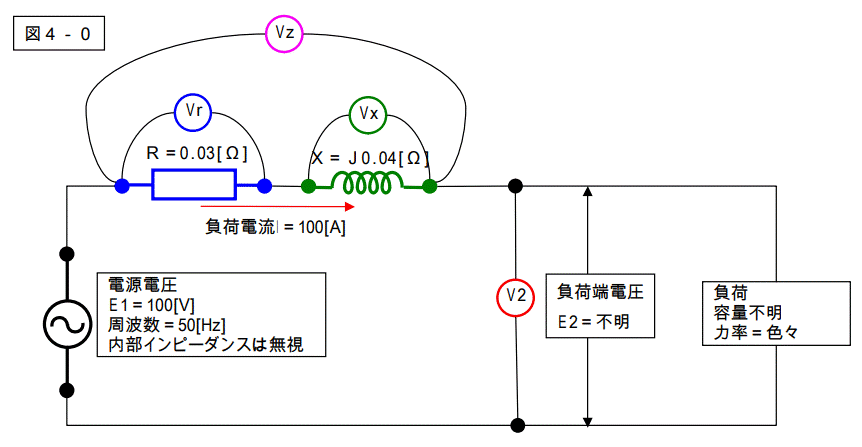
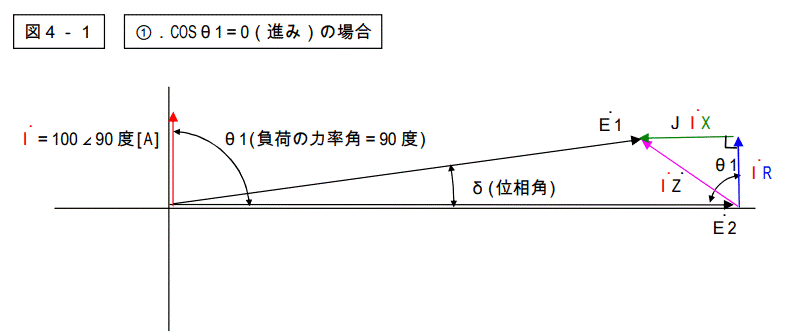
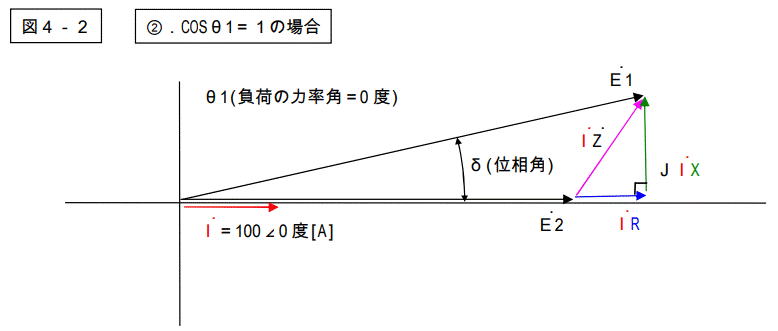
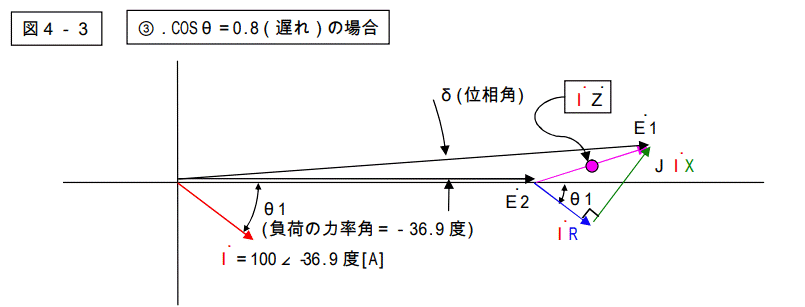
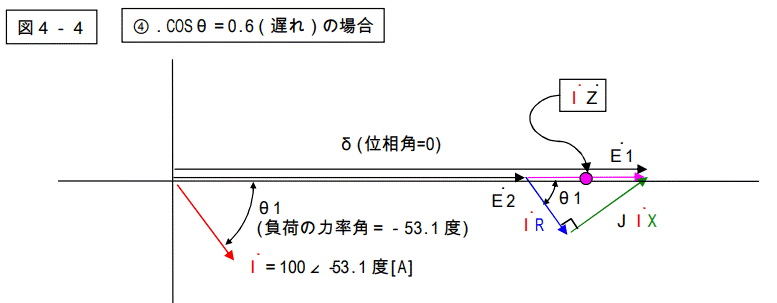
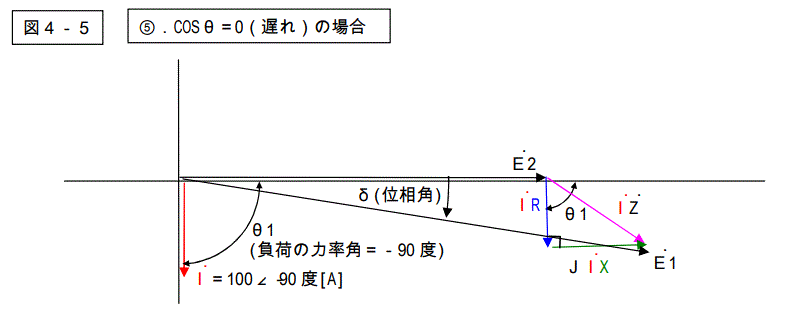
図4-1~5を見ると解りますが、電圧降下を表す三角形は総てのパターンで共通です。
大きさ、及び形は変わりません。力率角により、電源電圧に対する位相はずれて来ますが、形そのものは変わりません。
負荷力率の値は、短絡電流計算に無関係であることが解ります。
尚、当たり前の話ですが、この時、受電側の電圧は総て異なります。

- の値のことを、パーセント抵抗電圧(略してパーセント抵抗と言い %Rと書く。)、
- の値のことを、パーセントリアクタンス電圧(略してパーセントリアクタンスと言い %Xと書く。)
- の値のことを、パーセントインピーダンス電圧(略してパーセントインピーダンスと言い %Zと書く。)
と言います。
ですから、パーセントインピーダンスの値が解れば、短絡電流は簡単に計算出来ます。
しかし、ものの本を読むと「基準電圧」「基準容量」と言う単語が出てきます。
これは何を示しているのでしょうか?
因みに今回の場合は、基準電圧が 100[V]で、負荷電流が 100[A]ですから、基準容量は
基準容量[kVA]=100[V]×100[A]=10[kVA] となります。
「基準容量」という概念を理解するために下記の問題を解いて下さい。
【問題5】
下記の回路の%R、%X、%Zの値(スカラー値)を計算し、短絡電流を計算しなさい。
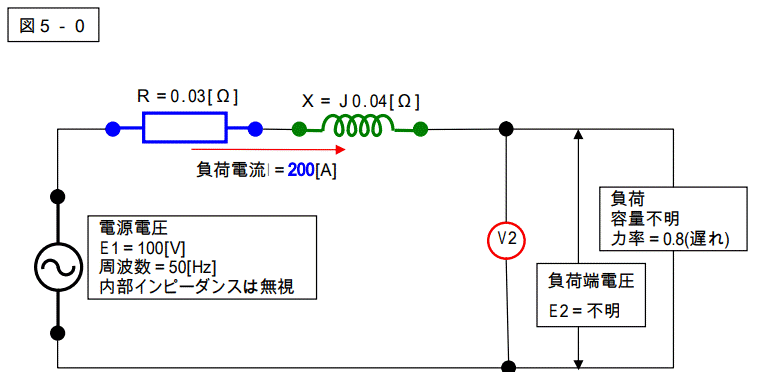
【解答5】
この問題は、問題2の電流値を変えただけの問題です。
単純に、負荷電流が2倍になっただけです。
従ってIR値、IX値、IZ値は簡単に計算出来ます。
IR値=電流値×抵抗値=200[A]×0.03[Ω]=6[V]
IX値=電流値×リアクテンス値=200[A]×0.04[Ω]=8[V]
IZ値=√(IR値 2+IX値 2)=√(62+82)=10[V]
%R値=IR値[V]÷電源電圧[V]×100[%]=6[V]÷100[V]×100[%]=6[%]
%R値=IX値[V]÷電源電圧[V]×100[%]=8[V]÷100[V]×100[%]=8[%]
%Z値=IZ値[V]÷電源電圧[V]×100[%]=10[V]÷100[V]×100[%]=10[%]
短絡電流=負荷電流÷%Z値=200[A]÷10[%]=2000[A]
【解説5】
計算結果を見ると解りますが、短絡電流の値は、問題2を元に問題4で解いた値と同じ値になります。
電源電圧が同じで、線路インピーダンスが同じですから、短絡電流は同じにならなければ理屈が合いません。
しかし、問題2と問題5では負荷電流の値が異なります。
この様に、パーセントインピーダンスを計算する時は、電源電圧及び負荷電流の値を明らかにしておかないと、意味を持たない数値になります。
つまり、何を基準にして、どの値とどの値の比率を取ったのか?を明らかにする必要が有ります。
この様な場合、電源電圧を「基準電圧」、負荷電流を「基準電流」と言います。
ここで、「基準電圧」と「基準電流」の単純積を計算したものを、「基準容量」と言います。
「基準容量」=「基準電圧」、×「基準電流」
単位は「kVA」です。
負荷力率は計算に関係がありませんので、kVA 値を捕まえておけば短絡計算は出来ます。
問題2では基準容量が 10[kVA]、問題5では基準容量が 20[kVA]です。
一般的に、「基準値」は「基準電圧」及び「基準容量」を明記します。
[基準電流]となる負荷電流はこの2つの値が解っていれば、簡単に計算出来ますので、通常は書きません。
パーセントインピーダンス値だけが解っても計算が成立しないことをご理解下さい。
必ず。「基準電圧」及び「基準容量」とセットです。
【問題6】
練習問題です。
下記回路の短絡電流(スカラー値)を求めなさい。
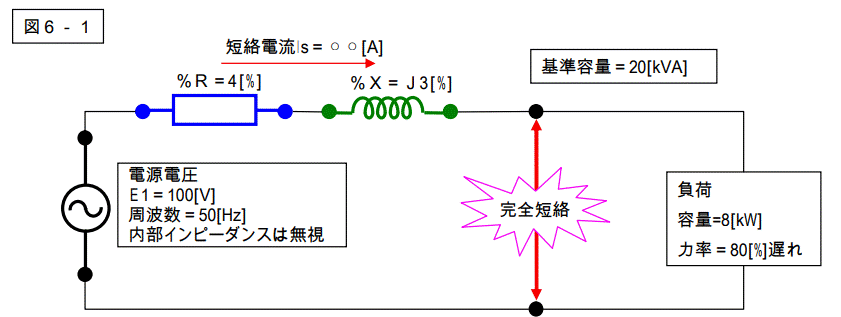
【解答6】
計算に当たり、無関係な数値が書かれています。
周波数=50[Hz]、負荷容量=8[kW]、負荷力率=80[%]は全く無関係です。ご注意下さい。
まず、基準となる電流値を計算します。
電源電圧が 100[V]ですから、基準電圧は 100[V]です。
従って、基準電流は
基準電流[A]=基準容量[kVA]÷基準電圧[V]=20[kVA]÷100[V]=200[A] となります。
パーセントインピーダンス%Zは%Z=√(%R2+%X2)=√(42+32)=5[%]
短絡電流=基準電流÷%Z=200[A]÷5[%]=4000[A] となります。
今回はパーセントインピーダンスの基本的な部分のみを記載しました。
これで、ご理解を賜れば幸いです。
それでもワカンナイ方、申し訳ありません、他の参考書をお読み下さい。




コメント