パーセントインピーダンス計算法(基礎編)
前回では、パーセントインピーダンス計算の初歩的な解説を記載しました。
今回はもう少し突っ込んだ話を記載します。
読者のご高覧を賜れば幸いです。

平成 鹿年 骨月 吉日
貧電工附属 サイタマ・ドズニーランド・大学 学長 鹿の骨
で・・・、毎度の様にいきなり問題を出します。
ここで前もってお断りを入れます。
X(エックス)と×(かけ算記号)ですが、非常に紛らわしく、事実上区別して記載出来ません。
従って次の様に書きます。
X(エックス)の場合 :X <==字の下に_を付ける。
×(かけ算記号)の場合:X <==そのまま。
【問題10】
下記回路で短絡事故が発生しました。
短絡電流Is1,Is2 を求めなさい。
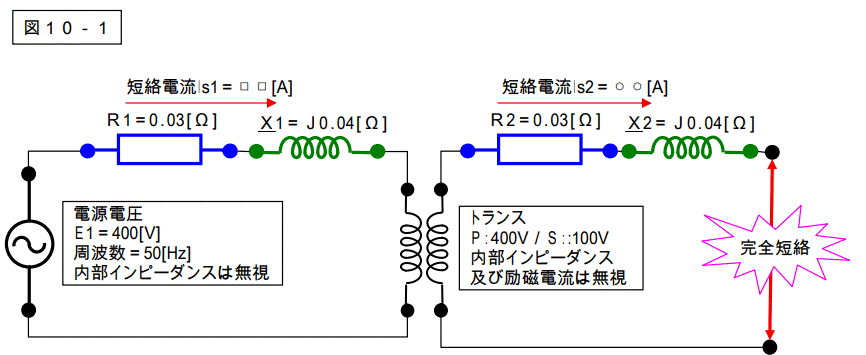
【解答10】
途中にトランスが入っている問題です。(オームインピーダンス法で解きます。)この様な問題を解くときは、トランスの二次側を一次側に又は一次側を二次側に変換します。
今回は二次側を一次側に変換してみましょう。(下図参照)
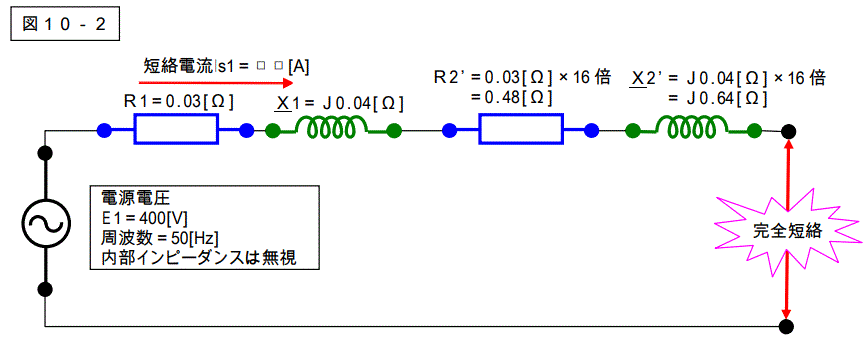
途中にトランスが入った場合、二次側のインピーダンスを一次側に変換する為には、二次側の値を巻き数比の2乗倍する必要が有ります。
このトランスの電圧比は 400V:100V ですから、巻き数比は 4:1 です。
ですから、二次側の値を 42 倍つまり 16 倍します。(詳細は最後のページに解説を記載しました。)
図 10-2 を整理すると下図になります。
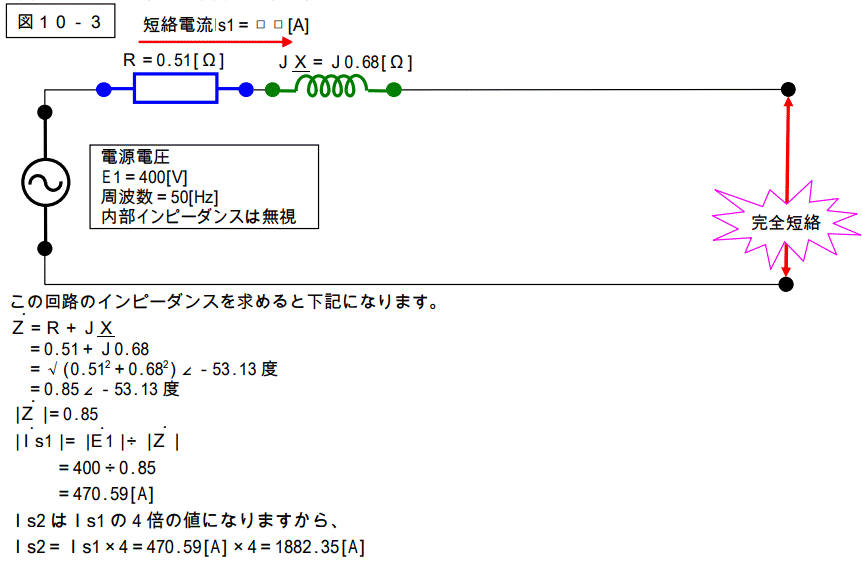
これで、答えは出ました。
引き続き、次の問題を解いて下さい。
(この問題をパーセントインピーダンス法で解くことを考えます。)
【問題11】
この回路の一次側の%R1、%X1、%Z1 の値及び二次側の%R2、%X2、%Z2 の値を求めなさい。
但し、基準容量は 10[kVA]とします。
【解答11】
一次側から求めます。
電源電圧が 400[V]で基準容量は 10[kVA]ですから、基準電圧及び基準電流は下記になります。
基準電圧=400[V]
基準電流=25[A](10[kVA]÷400[V]=25[A])
%R1 を求めます。
I1×R1=25[A]×0.03[Ω]=0.75[V](一次側抵抗分に依る電圧降下値)
%R1=I1×R1÷基準電圧×100[%]=0.75÷400×100=0.1875[%]
同様に%X1、%Z1 は
JI1X1=25[A]×J0.04[Ω]=J1.00[V](リアクタンスに依る電圧降下値)
J%X1=JI1×X1÷基準電圧×100[%]=J1.00÷400×100=J0.25[%]
%Z1=%R1+J%X1=0.1875[%]+J0.25[%]=0.3125∠53.13 度[%]
今度は二次側の計算です。
トランスの二次側電圧は 100[V]です。基準容量は 10[kVA]ですから、基準電圧及び基準電流は下記に
なります。
基準電圧=100[V]
基準電流=100[A](10[kVA]÷100[V]=100[A])
I2R2=100[A]×0.03[Ω]=3[V](二次側抵抗分に依る電圧降下値)
%R2=I2×R2÷基準電圧×100[%]=3÷100×100=3.00[%]
JI2X2=100[A]×J0.04[Ω]=J4.00[V]
J%X2=JI2X2÷基準電圧×100[%]=J4.00÷100×100=J4.00[%]
%Z2=%R2+J%X2=3.00[%]+J4.00[%]=5.00∠53.13 度[%]
これで一次側と二次側のパーセント値は総て出そろいました。
引き続き次の問題です。
【問題12】
トランスの一次側及び二次側のパーセントインピーダンス値を用いて、一次側に換算した合計パーセントインピーダンスを求め、この値を基に一次側の短絡電流を求めなさい。
【怪盗12】
ところで、合計パーセントインピーダンスってどうやって計算するの?
良くワカンナイので、苦し紛れに下記の計算を行います。
一次側に換算した合計%Z=一次側の%Z+二次側の%Z(単純和を取った。巻き数比?知るか!!)
=%Z1+%Z2
=0.3125∠53.13 度[%]+5.00∠53.13 度[%]
=5.3125∠53.13 度[%]
短絡電流は基準電流を%Zで割れば算出出来るので
Is1=25∠0 度[A]÷5.3125∠53.13 度[%]
=470.59∠-53.13 度[A]
答えが合っている!!。
引き続き次の問題です。
【問題13】
二次側の短絡電流を求めなさい。
【怪盗13】
同様に良くワカンナイので、苦し紛れに下記の計算を行います。
二次側短絡電流=二次側基準電流÷合計%Z値(合計%Z値は問題12の値そのままを使う。)
Is2=100∠0 度[A]÷5.3125∠53.13 度[%]
=1882.35∠-53.13 度[A]
これも答えが合っている。
苦し紛れに行った計算が合っている。
何でこうなるの?と言う話を次項に書きます。
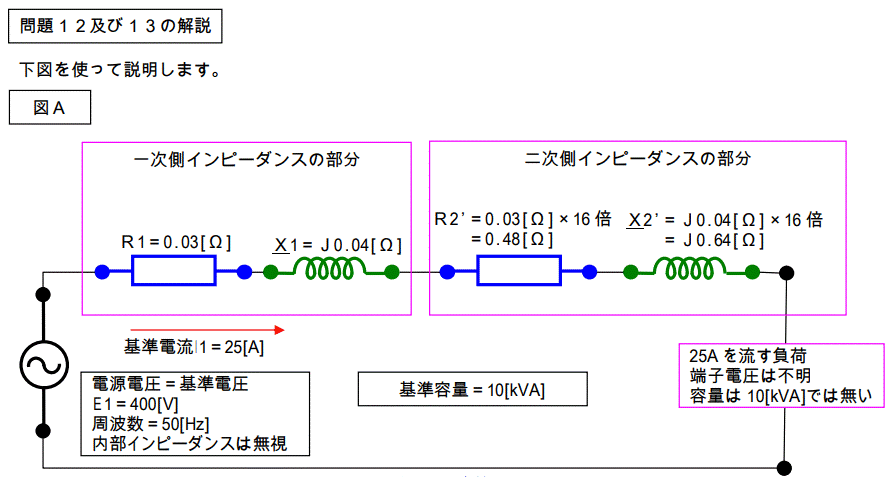
この図は回路を一次側に換算して、各インピーダンスを合算しないで描いたものです。
又、電流値はパーセントインピーダンスを計算するときに使用する基準電流をそのまま使っています。
ここで、計算される電圧降下の値と電源電圧との比率が、そのままこの回路の各々の部分のパーセントインピーダンスになります。
では計算してみましょう。
一次側インピーダンスの部分の計算
この計算は問題11で計算したものと全く同じです。結果のみを示します。
%Z1=%R1+J%X1=0.1875[%]+J0.25[%]=0.3125∠53.13 度[%]
二次側インピーダンスの部分の計算
基準電圧=400[V]
基準電流=25[A](10[kVA]÷400[V]=25[A])
抵抗分に依る電圧降下=I1R2’=25[A]×0.48[Ω]=12[V]
%R2’=I1R2’÷基準電圧×100[%]=12÷400×100=3.00[%] <==注目!!
リアクタンス分に依る電圧降下=JI1X2’=25[A]×J0.64[Ω]=J16.00[V]
J%X2’=JI1X2’÷基準電圧×100[%]=J16.00÷400×100=J4.00[%] <==注目!!
%Z2’=%R2’+J%X2’=3.00[%]+J4.00[%]=5.00∠53.13 度[%] <==注目!!
この回路は「一次側インピーダンスの部分」と「二次側インピーダンスの部分」が直列に接続された回路ですから、全体の%Zは各々の値の合算値になります。
%Z=%Z1+%Z2’=0.3125∠53.13 度[%]+5.00∠53.13 度[%]=5.3125∠53.13 度[%]
となりますので、一次側短絡電流Is1 は
Is1=一次側の基準電流÷%Z=25[A]÷5.3125∠53.13 度[%]=470.59∠53.13 度[A]
となります。(問題10と同じ結果になる。)
つまり、%R2=%R2’、%X2=%X2’、%Z2=%Z2’です。
二次側のパーセントインピーダンスの値はトランスの一次側に換算して計算しても、二次側でそのまま計算しても同じ値になります。
つまり、トランスがあっても無くても同じです。
何でこうなるの?巻き数比は何処へ行ったの?
【問題12及び13の解説の続き(最重要項目!)】
何やら不思議な計算結果になりました。
実計算を行った結果ですから、間違いは有りません。
しかし、納得がいかないと思います。
もう一度検証してみましょう。
二次側の各インピーダンス値と基準値を一次側に換算した各値との関係式は下記です。
R2’=R2 の 16 倍
X2’=X2 の 16 倍
I1=I2 の 1/4 倍
E1=E2 の 4 倍
定義式に則り、二次側を一次側に換算したパーセント抵抗電圧(%R)の計算は下記になります。
(%R2’の計算です。)
%R2’=一次側基準電流×二次側の抵抗分を一次側に換算した値÷一次側の基準電圧×100[%]
=I1×R2’÷E1×100[%]
この式に上の関係式を代入すると下記になります。
=I2 の 1/4 倍×R2 の 16 倍÷E2 の 4 倍×100[%] <=巻き数比はキチンと計算されている!!
=I2×R2÷E2×100[%]×(1/4 倍×16 倍÷4 倍)
=I2×R2÷E2×100[%]×1倍 <=巻き数比を弄くり廻して最後には1倍になる!!
=I2×R2÷E2×100[%]
=二次側の基準電流×二次側の抵抗値÷二次側の基準電圧×100[%]
=%R2(二次側で計算したパーセント抵抗電圧)
%R2’=%R2 が証明されました。
と言うことで、二次側を一次側に換算して計算した結果と、二次側をそのまま計算した結果は、同じ値になります。%Xの計算も同じ結果になりますし、%Zの計算も同じ結果になります。
又、一次側を二次側に換算した結果も同じです。
計算略(各自試みよ。)
この結果は非常に重要です。
パーセントインピーダンス法で計算すれば、短絡電流の計算では、途中にトランスが有っても無くても計算には関係が有りません。
つまり計算が楽な訳です。
ですから、一般的に短絡計算はパーセントインピーダンス法が用いられます。
次のおまけも読んでね。
トランスのインピーダンス変換の話
トランスの一次側を二次側に、或いは二次側を一次側に変換する場合の変換の仕方の話です。
此処で言うトランスは下記の様なものを示します。
この様なものを「理想トランス」と言います。
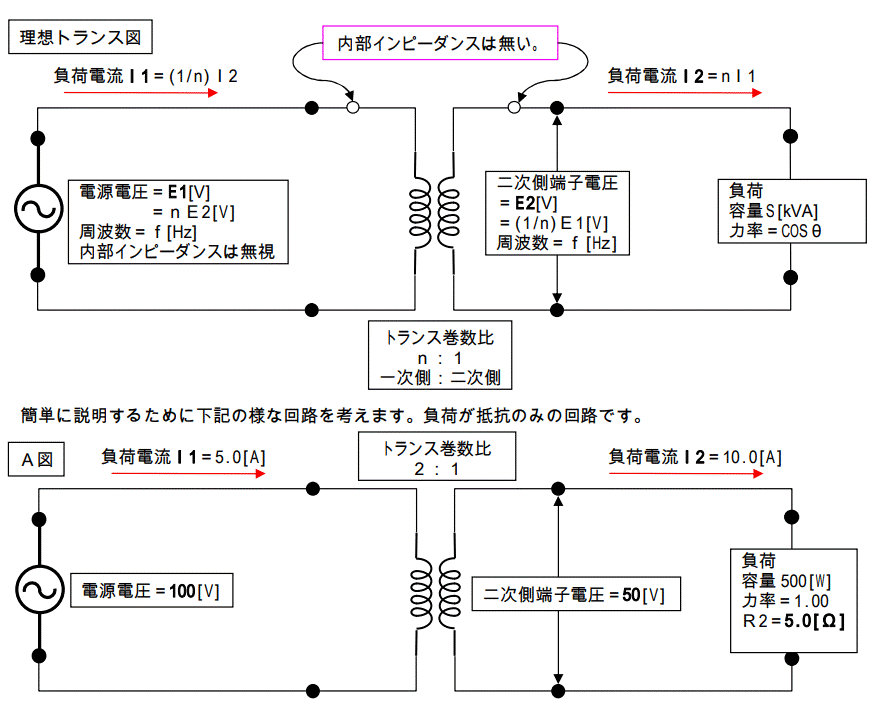
各数値は暗算で計算出来ると思います。
この負荷を一次側に換算すると下図になります。
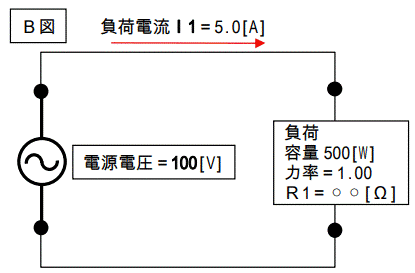
さて、この図で○○[Ω]の部分は幾つになるでしょうか?
二つの図で共通で無ければならないものは消費電力500[W]です。
B図に於いて、消費電力を示す式を立てます。
W=I12R1
500=5.02R1
R1=500÷5.02
=25[Ω]
R1 とR2 を見比べると
R1 はR2 の4倍であることが解ります。
巻数比は「2」ですが、この倍数は「22」倍になっています。つまり、二次側インピーダンスを一次側に変換する場合は、巻数比の2乗倍する必要が有ります。
一次側を二次側に変換する場合はこの逆で1/巻数比の2乗倍になります。
これで納得出来ない人は次ページ以降を根性で読むべし。
トランスのインピーダンス変換の話その2
トランスの等価回路は回の様になっています。
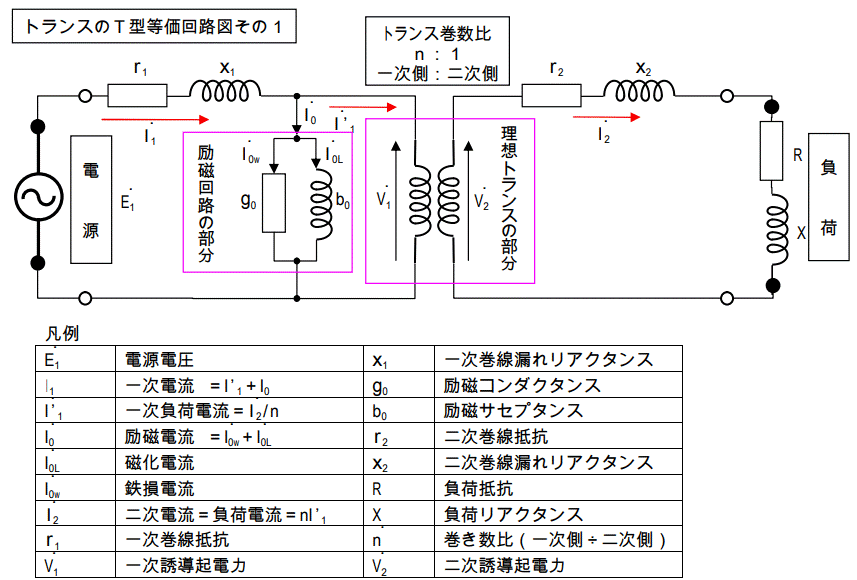
ナンジャコリャ・・と思ったアナタは普通です。
こんな複雑怪奇な回路を普通に扱うことは普段はありません。余り細かい所は気にしないで下さい。
さて、この回路の二次側を一次側に換算すると下図になります
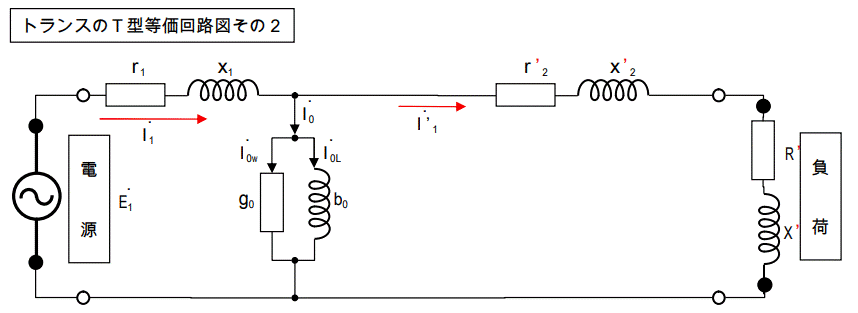
二次側の巻線抵抗、漏れリアクタンス、負荷抵抗、負荷リアクタンスを一次側に換算しました。
各々「’」を付けてあります。
この「’」が付いた値と元々の値の関係を調べれば良いわけです。
尚、負荷電流は一次側の負荷電流がそのまま流れますから同じ値になります。
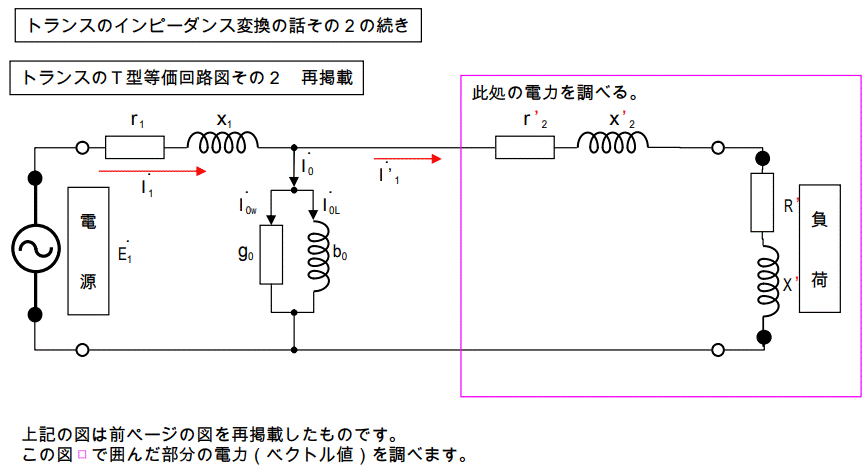
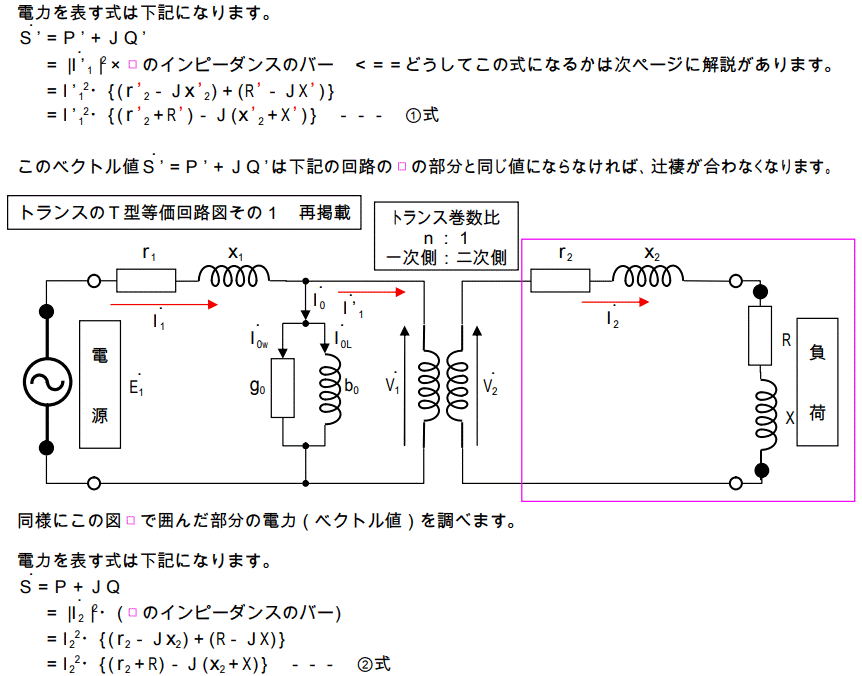
①式と②式が同じ値を取らなければ、この等価回路はインチキになってしまいます。

電力のベクトル値の求め方

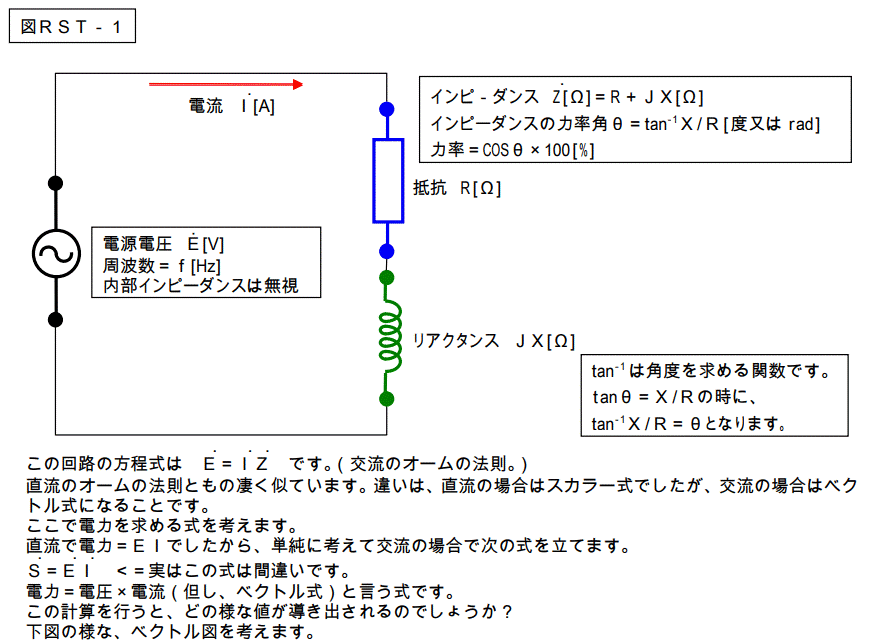
この回路の回路の方程式はE=IRです。(オームの法則のまんま!)
電力=EI=I2
Rです。(いくら何でもこれがワカランとは言うなよ!)
実はこの関係式は交流の場合でも当てはまります。
交流の場合でも当てはまります、と言うことで、次の様な回路を考えます。
基本的な交流回路です。
インピーダンスは抵抗とインダクタンスの組み合わせです。
つまりこのインピーダンスのリアクタンスは遅れです。
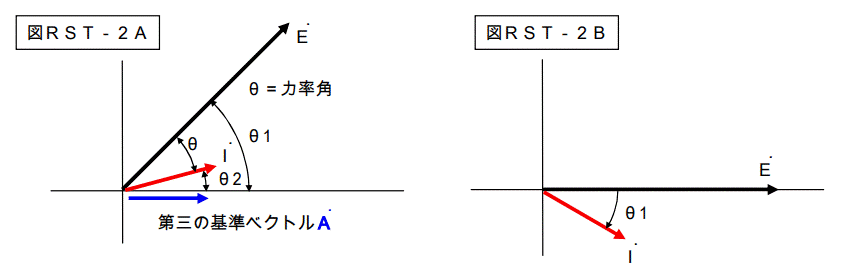
図RST-2Aはかなり変則のベクトル図です。普通は図RST-2Bで書きます。
しかし、今回は説明の都合上、図RST-2Aで説明を行います。


本日の講義はこれでオシマイ
パーセントインピーダンス計算法(基礎編 その2)
前回では、パーセントインピーダンス計算の初歩的な解説と基礎を記載しました。
今回はこれらが理解できているかの検証です。
読者のご高覧を賜れば幸いです。

平成 鹿年 骨月 吉日
貧電工附属 サイタマ・ドズニーランド・大学 学長 鹿の骨
ここで前もってお断りを入れます。
X(エックス)と×(かけ算記号)ですが、非常に紛らわしく、事実上区別して記載出来ません。
従って次の様に書きます。
X(エックス)の場合 :X <==字の下に_を付ける。
×(かけ算記号)の場合:X <==そのまま。
早速ですが下記の問題を考えてください。
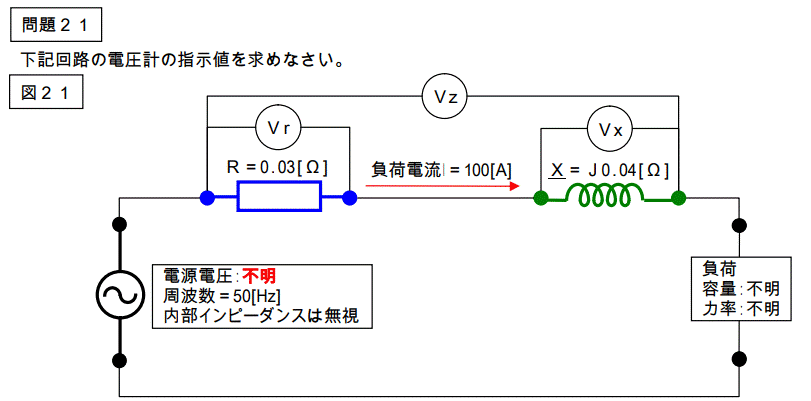
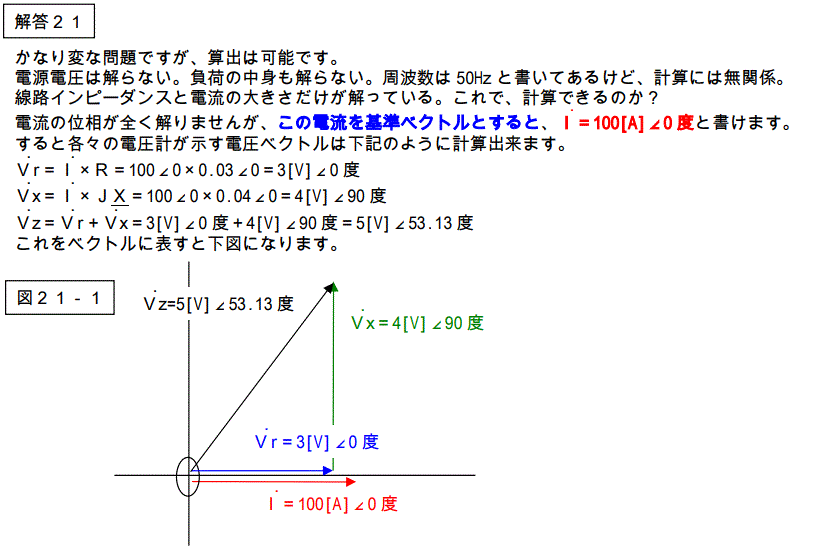
今度は下記の問題を考えてください。電源電圧の値が与えられています。
【問題22】
下記二種類の回路の%Z、%R、%Xの値を求めなさい。
又、負荷端で短絡事故が発生した時の短絡電流を%Zを使って求めなさい。
又、短絡電流計算を行った時の基準容量を示しなさい。
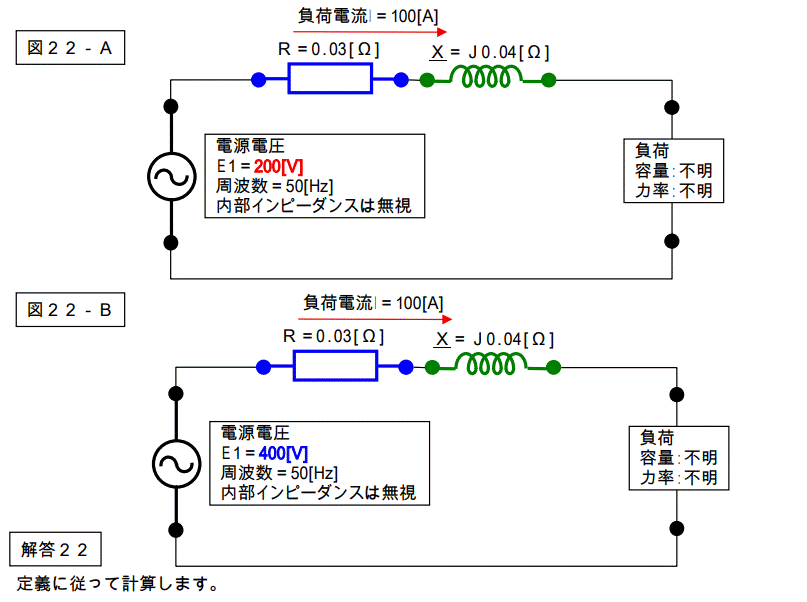

3つ目の問題です。(理想)トランスが絡んでいます。
【問題23】
下記回路のトランス一次側の負荷電流 I1 を求めなさい。
%Z、%R、%Xの値を求めなさい。
又、負荷端で短絡事故が発生した時の短絡電流を%Zを使って求めなさい。
尚、400V の配線部分ではインピーダンスは無いものとし、トランスのインピーダンスも全て無視する。
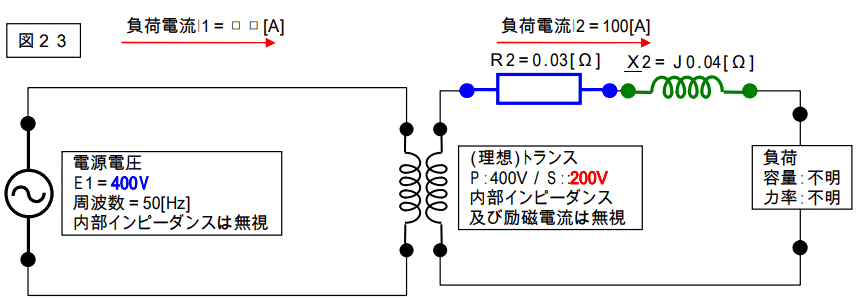
【解答23】
何かヘンな問題です。
トランス一次側の負荷電流 I1 を聞いていますのでこれを計算します。
I1=暗算で 50[A]です。(幾ら何でもこれがワカランとは言うなよ。)
さて%Rの計算から始めますが。分子のIR[V]の計算はすぐに出来ます。
IR=100[A]×0.03[Ω]=3.00[V]です。
分母は 200V?400V どっちだ?
取り敢えず 200[V]で計算して見ましょう。
%R=100[A]×0.03[Ω]÷200[V]×100[%]=1.5[%]
同等に、%X=2.00[%]、%Z=2.50[%]
問題22のAの場合の結果と全く同じです。
二次側の短絡電流 Is2 を計算すると
Is2=基準電流÷%Z×100 倍=100[A]÷2.50[%]×100 倍=4,000[A]
これも同じ答えになります。(当たり前じゃん!!)
トランス一次側は、電圧が2倍ですから、一次側短絡電流 Is1 は Is2 の半分です。
Is1=Is2×(200[V]/400[V])=4,000[A]×0.5=2,000[A]となります。ウン正解だぁ~!!
これで解けたからOKではありません。
400[V]で計算したらどうなるかをやって見ましょう。
%R=100[A]×0.03[Ω]÷400[V]×100[%]=0.75[%]
同等に、%X=1.00[%]、%Z=1.25[%]
この値を使って Is1 を求めます。
(基準電圧にトランスの一次側の電圧を使っているから、一次側の電流が先に算出出来ると思いこんで計算する。)
Is1=基準電流÷%Z×100 倍=100[A]÷1.25[%]×100[倍]=8,000[A]
あれまぁ~・・・値が4倍狂っています。
何でこんな結果になるのか?
ここで基準容量を思い出してください。
この問題の基準容量は 20,000[VA]です。
二次側 200V]×100[A]=基準容量 20,000[VA]=一次側 400[V]×50[A]
上の式で 400V を元に計算したものはこの基準容量を無視しておかしな計算をした結果です。
基準容量を元に計算した場合、400[V]の場合基準電流は 50[A]でなければイケナイ事になります。
この値を使って計算した結果を次項に示します。
%Zの値はトランスの一次側でも二次側でも同じですから、短絡電流の計算には好都合な訳です。
二次側で計算した%Zは 2.50[%]でした。
この値を算出した時の電流は 100[A]で、電圧は 200[V]でした。
従って、基準電流=100[A]、基準電圧=200[V]となり、基準容量=20[kVA]となります。
一次側の計算をする時に、この基準容量を変えてはイケマセン。
一次側も二次側も基準容量=基準容量=20[kVA]で同じです。
一次側の基準容量を 20[kVA]とすると、自動的に基準電圧は 400[V]、基準電流は 50[A]となります。
短絡電流=基準電流÷%Z の計算を一次側の数値で計算すると下記になります。
Is=50[A]÷2.50[%]=2000[A] という結果が得られます。
わかったぁ~・・・かな?
さて、理解を確実にするために次の問題を解いて下さい。
これがスラスラ解ければOKです。
【宿題】
下記の回路の%R、%X、%Z及び負荷端で短絡した時の短絡電流を求めなさい。
尚、基準容量は自分で設定し、その値に対する%Z値を示しなさい。
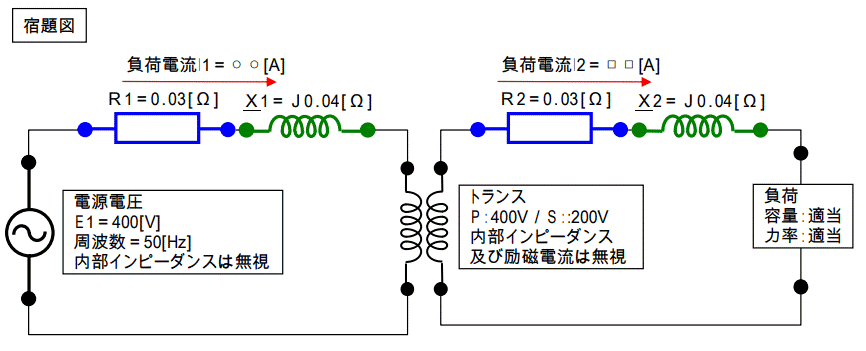


となりますので、短絡電流の計算結果は同じ結果が得られます。
途中式で、%Zの値が 100[%]を超えますが、この様な場合もあります。
計算間違いではありません。
検算は各自オームインピーダンス法を用いて試みてください。
最後に次の問題を考えてください。
相当に厄介な問題です。
【問題24】
下記の回路負荷端で短絡した時の短絡電流を%Zを使って求めなさい。
尚、基準容量は 100[kVA]とします。
(電圧値、インピーダンスの値が前の問題とは違うので注意する事。)
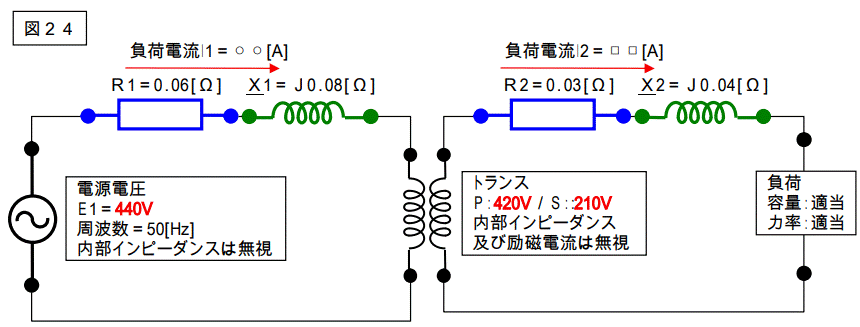
計算を始める前にオームインピーダンス法を使って、正解の値を先に求めておきます。
上記図を下図のように変換します。(一次側に変換する。)
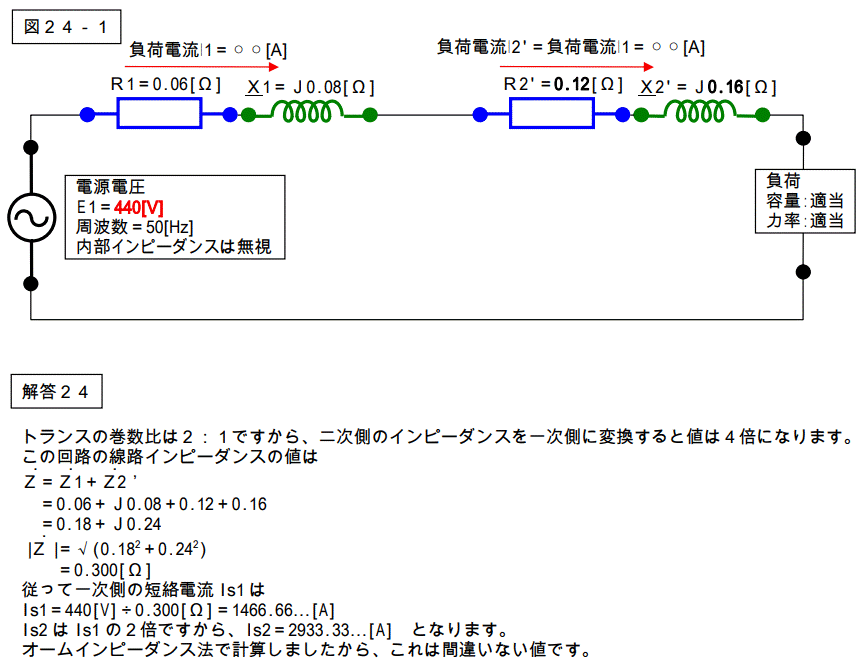
ではパーセントインピーダンス法でやってみましょう。
まず、基準容量を決めます。基準容量は 100[kVA]とします。
基準電圧、基準電流は下記のようになります。
下記の計算は間違っています。何処が間違っているのか考えてください。


今度は同じ結果になりました。何でこうなるの?????
理由はとにかく、どうやら二次側の基準電圧の取り方がおかしかったようです。
気を取り直してもう一度トライします。
基本的な疑問として 220[V]って何処の値だ?という疑問が残ります。
実はこの値は、この回路の無負荷時のトランス二次端子電圧です。
今度は二次側の基準電圧を 220[V]で計算してみましょう。

めでたく正解にたどり着きました。(フゥ~ヤレヤレ・・)
ところでこれで理解できましたか?
多分・・・「ワケガワカラン」という事だと思います。
こうやってシャーシャーと書いている当の本人も、計算が合わなくて何回も計算を行いました。
間違った計算を行った場合の等価回路を次ページに幾つか示します。
これで理解を得られれば幸いです。
【間違い計算例 その1】
一次側の基準電圧を 440[V]、二次側の基準電圧を 210[V]として計算した場合は、下図の回路の計算をした事になります。
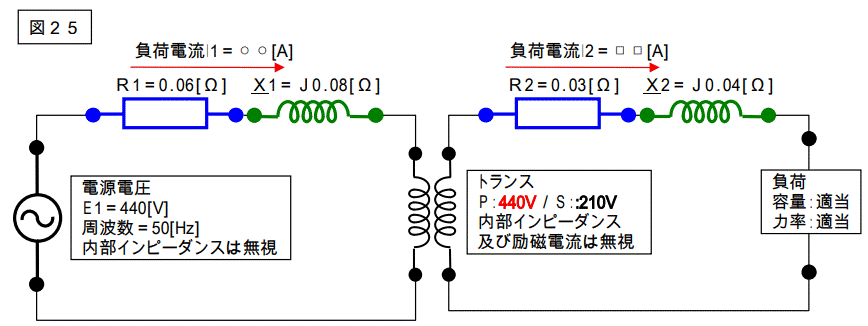
これはトランスの変圧比を間違えて計算した事になってしまいます。
上記の回路の短絡電流をオームインピーダンス法で解いてみましょう。
変圧比は 440:210 ですから、44/21:1 です。
この回路図を一次側に換算すると下図のようになります。
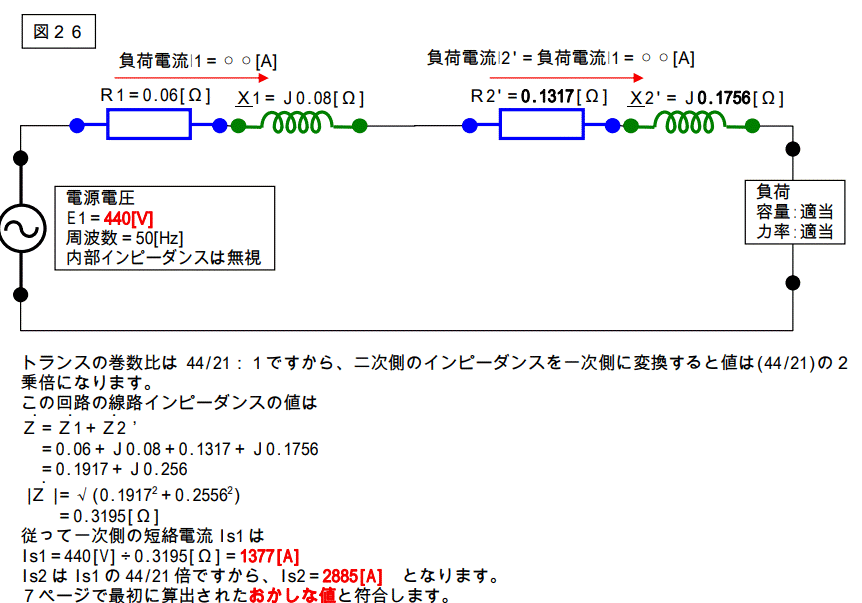
【間違い計算例 その2】
一次側の基準電圧を 420[V]、二次側の基準電圧を 210[V]として計算した場合は、下図の回路の計算をした事になります。
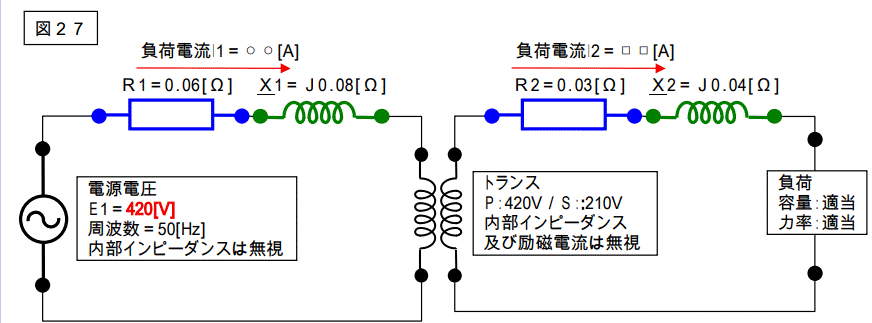
これは電源電圧を間違えて計算した事になってしまいます。
同様に上記の回路の短絡電流をオームインピーダンス法で解いてみましょう。
変圧比は 420:210 ですから、2:1 です。
この回路図を一次側に換算すると下図のようになります。
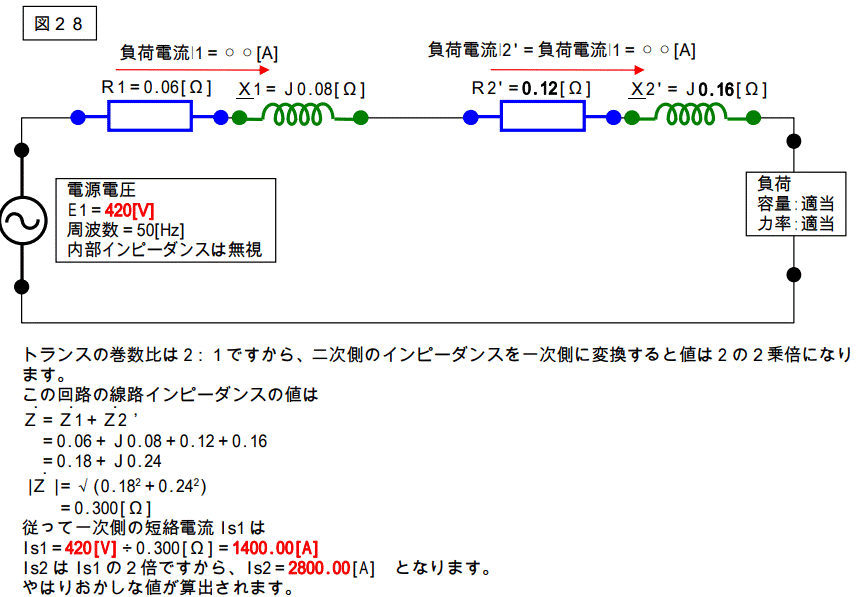
わかったぁ~・・・かな? 多分、未だモヤッとしているのでは?
駄目押しで下記の説明をご覧下さい。
下図は図24のままです。
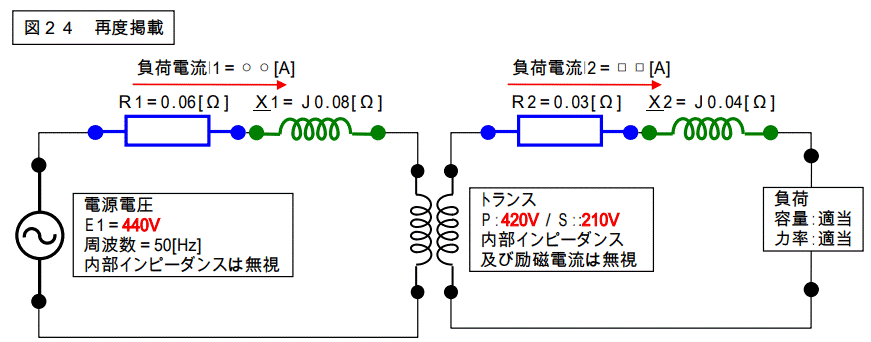
一次側回路定数を二次側に変換します。
トランスの巻数比は2:1ですから、一次側の値は二次側に変換すると1/4になります。下図参照。
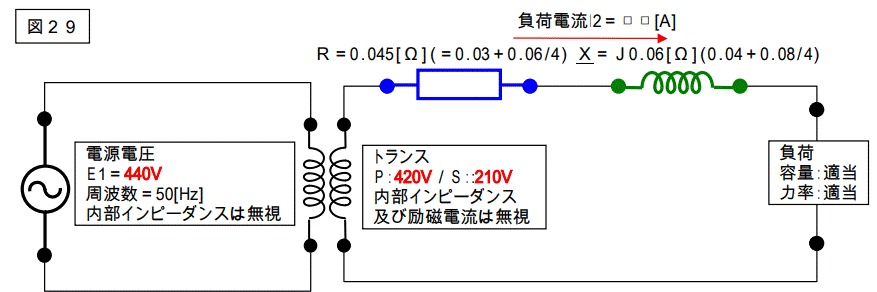
この時にトランスに加えられる一次電圧は幾つか?
420V?・・・NO!! 440V です。
トランスの巻数比は2:1ですから、二次側の電圧は 210V ではなく 220V になります。
このことから、二次側の基準電圧は 210V ではなく、220V としなければならない事が解ります。
トランスの変圧比はP:420V/S::210V で与えられますが、この値をこのまま基準電圧として計算するのではなく、220V の値を算出するための手段として用います。
多分、アタマの中はグルングルンだと思います。
じっくり考えて、確実に理解してください。
(次項はおまけです。)
この様に途中でトランスが入った場合、変圧比を注意深く見ないと計算違いをしでかす事になります。
この例題で示した様な、一次側電源電圧とトランスの一次電圧が異なる場合は、日常的にあり得る事です。
下記のような電流が流れた場合を解析してみましょう。(結構難しいですよ。)
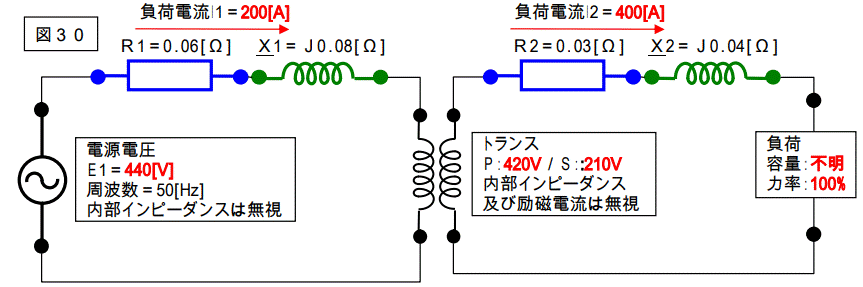
解りやすいようにオームインピーダンス法で解いてみましょう。
この回路図を一次側に換算すると下図のようになります。
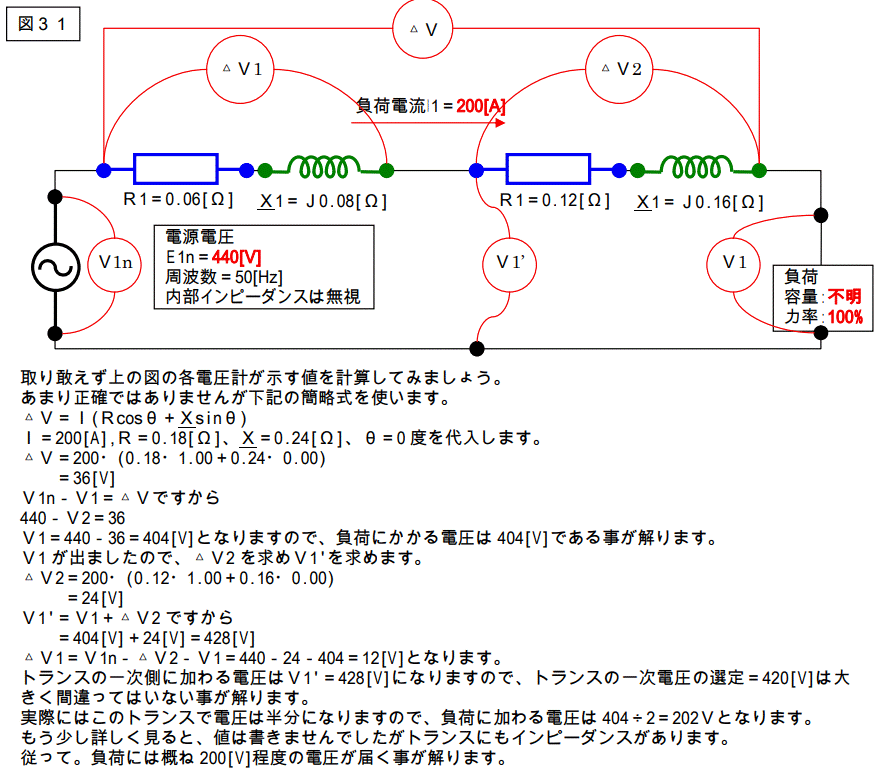
【オシマイ】


コメント