地絡事故発生時の地絡電流を検出する地絡保護用に使用するZCT(Zero-phase Current Transformer)について、その動作原理をベクトル図を使って解説を頂いています。零相変流器は電流のアンバランスを検出(打ち消さない成分を取り出す)変成器ですが、単なる不平衡負荷ではZCT2次側には電流は流れません。
電流ベクトルについて、「閉じたベクトル」の概念・原理を対象座標法を用いず解説を頂いた資料になります。
こちらの記事は「鹿の骨」さんにご投稿いただいた貴重な資料です。いつもありがとうございます。
ZCTの動作原理の話
dende さんこんにちは
今回のお題はZCTの動作原理です。
普段よく見かける電気機器ですが、基本的な所をおさらいしましょう。

平成 鹿年 骨月 吉日
貧電工附属 さいたまドズニーランド大学 学長 鹿の骨
ZCTは漏電を検出する非常に大事な電気機器で、低圧高圧特別高圧など交流回路の色々な所で使用されています。
ZCTは、ZCTを貫通している電線に流れている電流のベクトル和がゼロになるかならないかを検出します。
電流のベクトル和がゼロになると、ZCTに誘電する起電力がゼロになりますので、ZCTには電流が流れません。
つまり、下図のような話です。
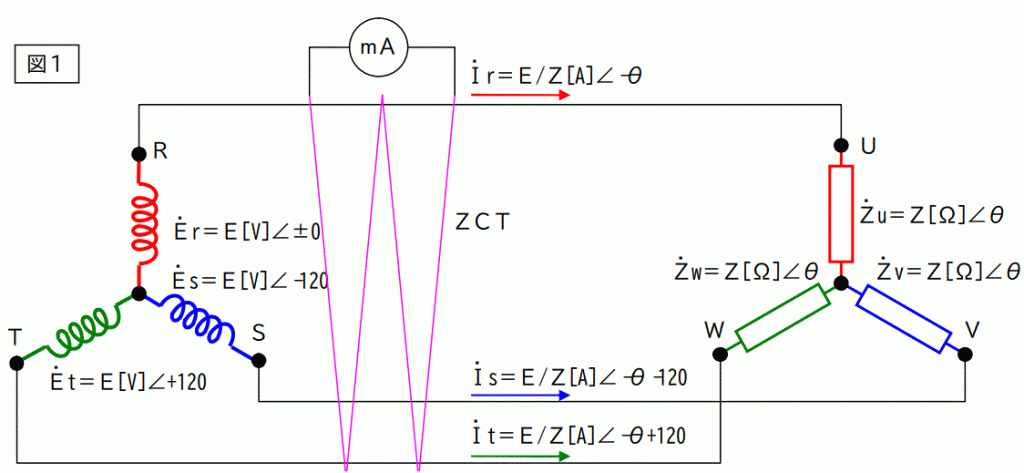
三相平衡電圧電圧電源に三相平衡負荷を接続すると三相平衡電流が流れ、線電流のベクトル和はゼロになる。従って、ZCTに流れる電流はゼロになるので漏電では無いことが解る。
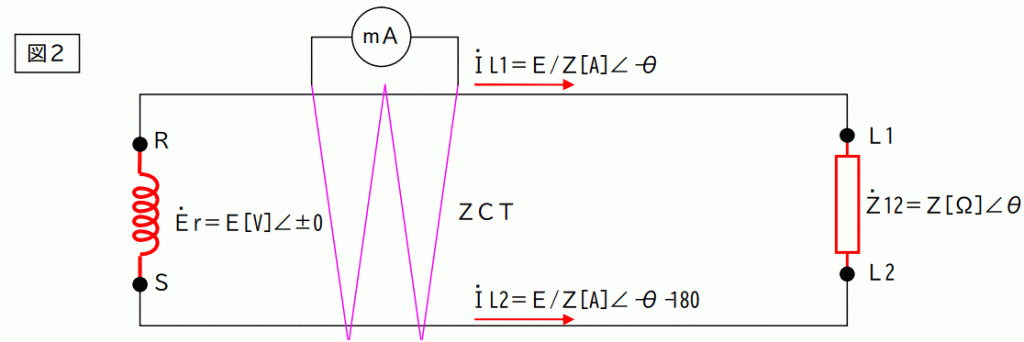
単相の場合、図の様に電流方向を定義する。
負荷から電源に帰る電流を←の方向に取り、IL1=E/Z[A]∠-θとしてしまうと、行きと帰りの電流のベクトル和が次のような式になり、混乱する。
2線の電流のベクトル和=E/Z[A]∠-θ+E/Z[A]∠-θ=2E/Z[A]∠-θ ? <==ナンジャコリャ
三相の場合と同様に、電源から出ていく方向を正方向として、電流を定義する。
電流のベクトル和=IL1+IL2=E/Z[A]∠-θ+E/Z[A]∠-θ-180=0
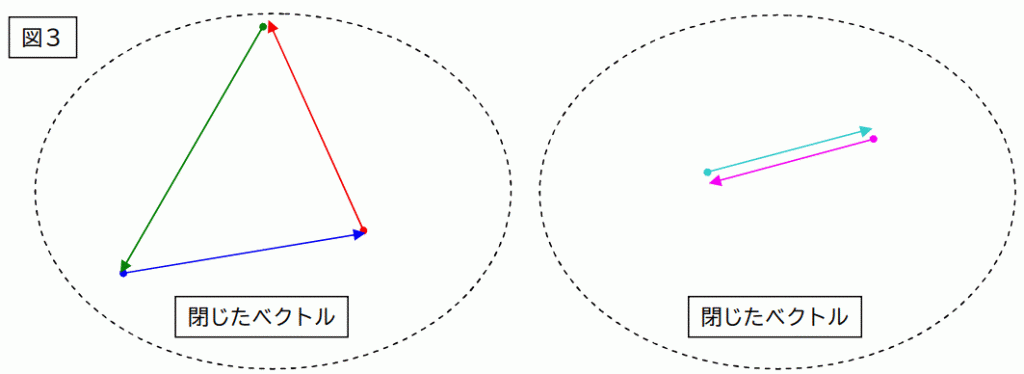
「閉じたベクトル」+「閉じたベクトル」も「閉じたベクトル」になります。
下図のようにどの様な配置にしても必ず閉じます。(和がゼロになる。)
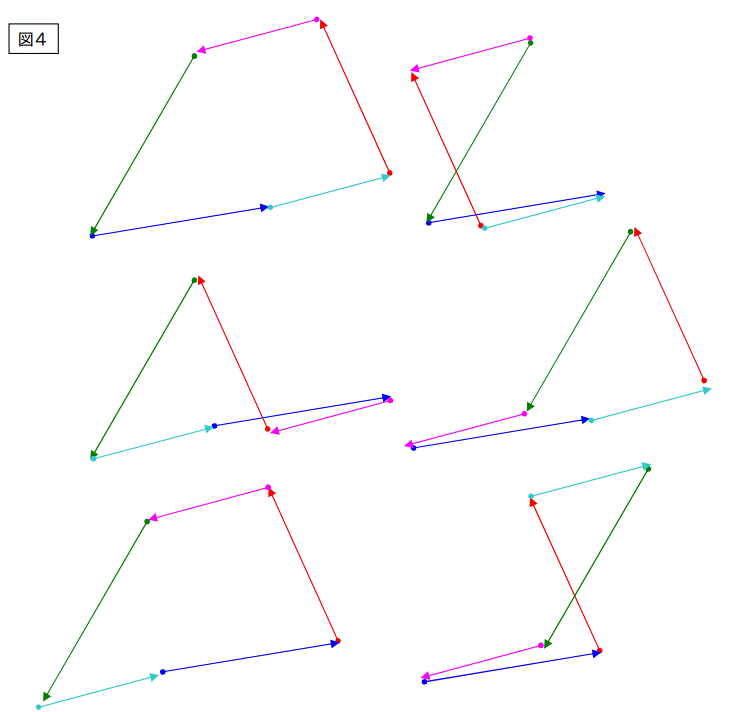
三相電流は必ず閉じるように流れます。(閉じなかったら漏電。)
不平衡負荷でも、電流ベクトルが閉じる例を提示します。
下図のような場合で考えてみましょう。
電源は三相平衡電圧電源です。線路のインピーダンスは無視します。
図のように負荷が不平衡でデルタに組まれた場合です。
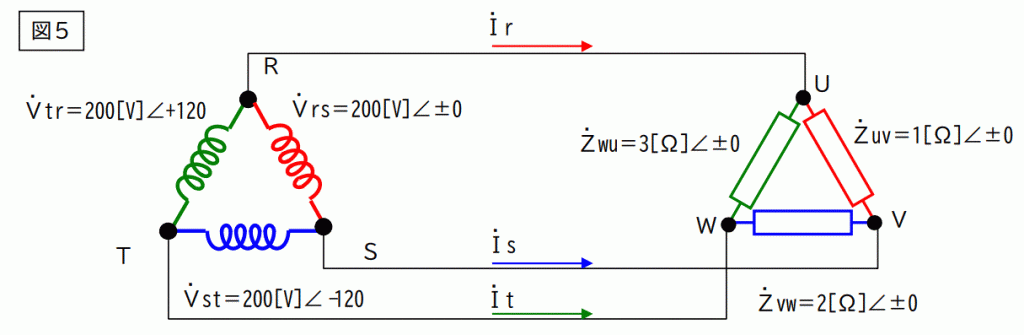
この図を下図のように分解します。
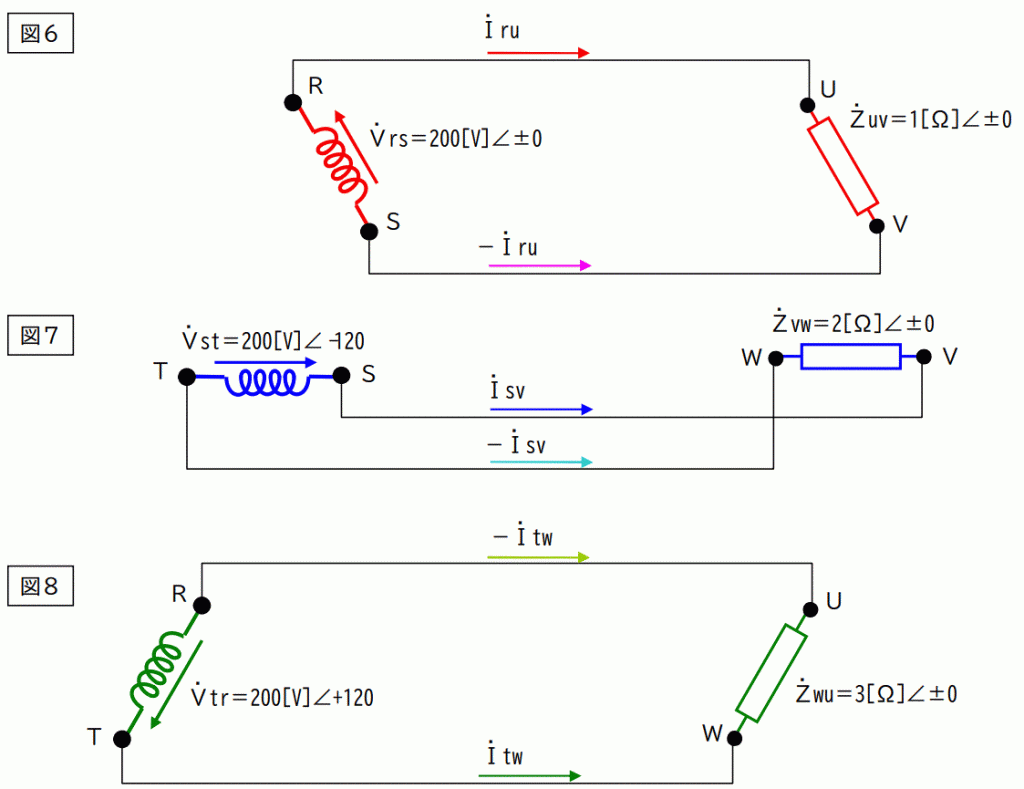
一見不思議に思えるかも知れませんが、この図は「重ねの理」の逆を書いたものです。
つまり図5=図6+図7+図8です。
次ページでこの電流値の計算を行います。
Iru を計算します。
Iru=Vrs÷Zuv=200[V]∠±0÷1[Ω]∠±0=200[A]∠±0
-Iru=200[A]∠180
同様に
Isv=Vst÷Zvw=200[V]∠-120÷2[Ω]∠±0=100[A]∠-120
-Isv=100[A]∠60
Itw=Vtr÷Zwu=200[V]∠120÷3[Ω]∠±0=66.7[A]∠120
-Itw=66.7[A]∠-60
これら6つの電流の和は幾つになるのでしょうか?
計算するまでも有りません。和は「ゼロ」です。
従って下図のような回路が描けます。
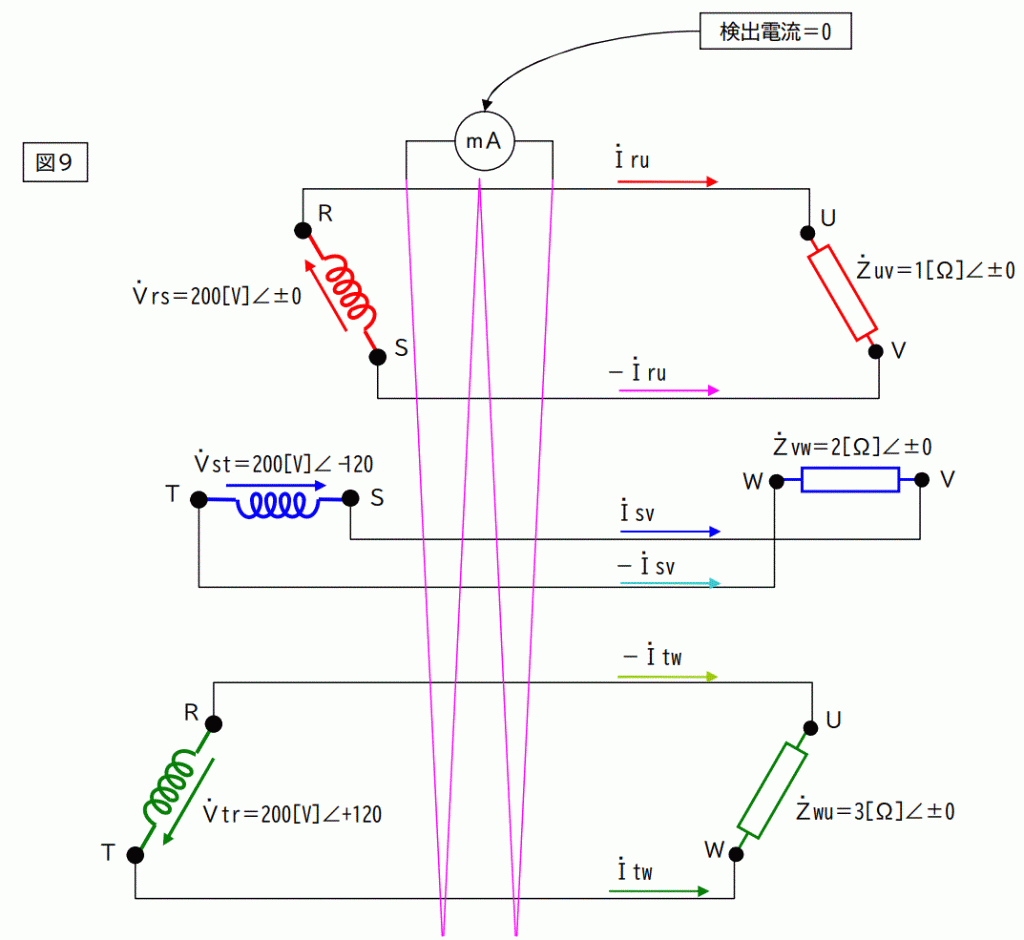
さて、バラバラにした回路の電流和はゼロになりました。
今度はこれを元の回路に戻して検討して見ましょう。
次ページで、この回路図を元に戻します。
下図は途中経過を示す図です。
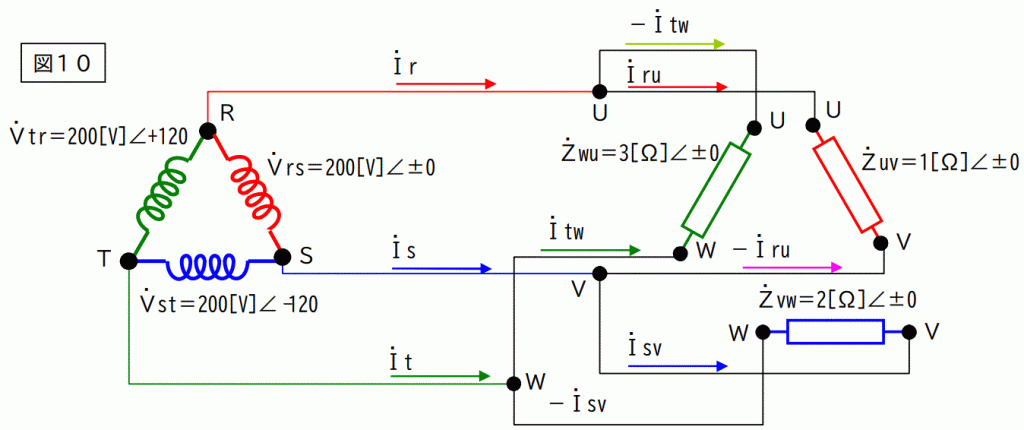
図から解るとおり下記の関係式が導き出されます。
Ir=-Itw+Iru
=66.67∠-60+200∠±0
=66.67(1/2-J√3/2)+200(1+j0)
=33.34-J57.73+200+J0
=233.34-J57.73
=240.37∠±0-13.9
Is=Isv+(-Iru)
=100∠-120+200∠180
=100(-1/2-J√3/2)+200(-1+j0)
=-50-J86.6-200+J0
=-250-J86.6
=264.57∠-199.11=264.57∠-120-79.11
It=Itv+(-Isv)
=66.7∠120+100∠60
=66.7(-1/2+J√3/2)∠120+100(1/2+J√3/2)
=-33.34+J57.73+50+J86.6
=16.66+J144.33
=145.29∠83.42=145.29∠+120-36.58
この3つの電流のベクトル和は
ΣI=Ir+Is+It
=233.34-J57.73-250-J86.6+16.66+J144.33
=0+J0
となりますので無事この電流ベクトルは閉じます。
値を記載した回路図を下図に示します。

今度はスターの場合です。電圧は少し変えて有ります。
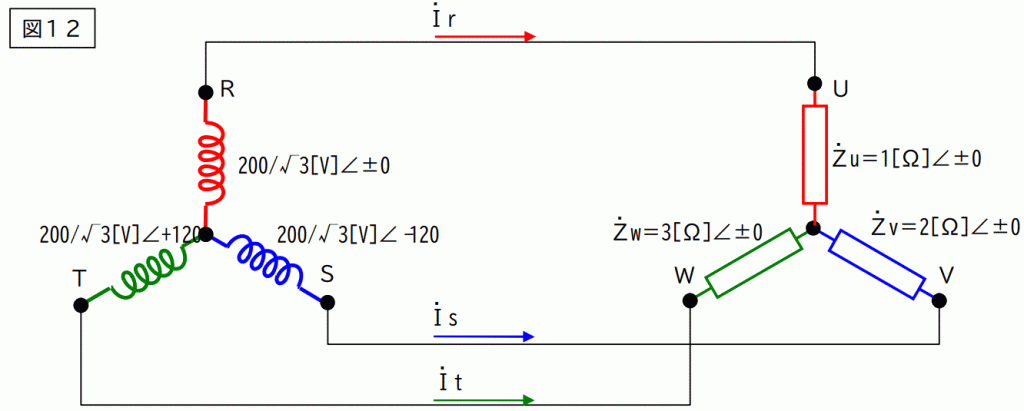
立てる方程式は下記
Ir+Is+It=0
IrZu+IsZv+ItZw+3Vnn’=0
しかし、このままでは解けません。苦肉の策で上図を下図のように変換します。
インピーダンスのスターデルタ変換。

図11において、下記の方程式が成立します。
Iuv=200∠30 度[V]/11/3[Ω]
Ivw=200∠-90 度[V]/11[Ω]
Iwu=200∠150 度[V]/11/2[Ω]
これを解いて下記を得る。
Iuv=200(√3/2+1/2)/11/3
=300√3/11+j300/11[A]
Ivw=200(0-j1)/11
=0-j200/11[A]
Iwu=200(-√3/2+j1/2)/11/2
=-200√3/11+j200/11[A]
線電流は下記の関係式になります。
Ir=Iuv-Iwu
Is=Ivw-Iuv
It=Iwu-Ivw
これを解いて下記を得る。
Ir=300√3/11+j300/11-(-200√3/11+j200/11)
=78.73+j9.09
Is=-j200/11-(300√3/11+j300/11)
=-47.24-j45.45
It=-200√3/11+j200/11-(-j200/11)
=-31.49+j36.36
Ir+Is+It=0 <==O
宿題です。
前述のデルタの場合、及びスターの場合は、実値を計算したものです。
インピーダンスの値を一般記号Z1,Z2,Z3 とし、如何なる場合でも電流ベクトルが閉じることを証明
して下さい。
尚、電源は三相平衡電圧電源とし、スター結線でもデルタ結線でも結構です。
【宿題解答編】電流ベクトルが閉じることの証明
宿題の解答です。
電源はスターでもデルタでも良いと言っていますので、都合の良い方を選びます。
デルタで考えてみましょう。
負荷のインピーダンスがデルタに接続された場合からスタートします。
下図のような回路になります。
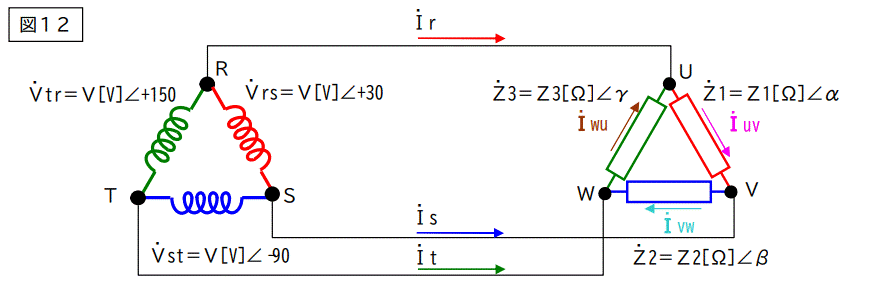
この回路を下図のように分解します。
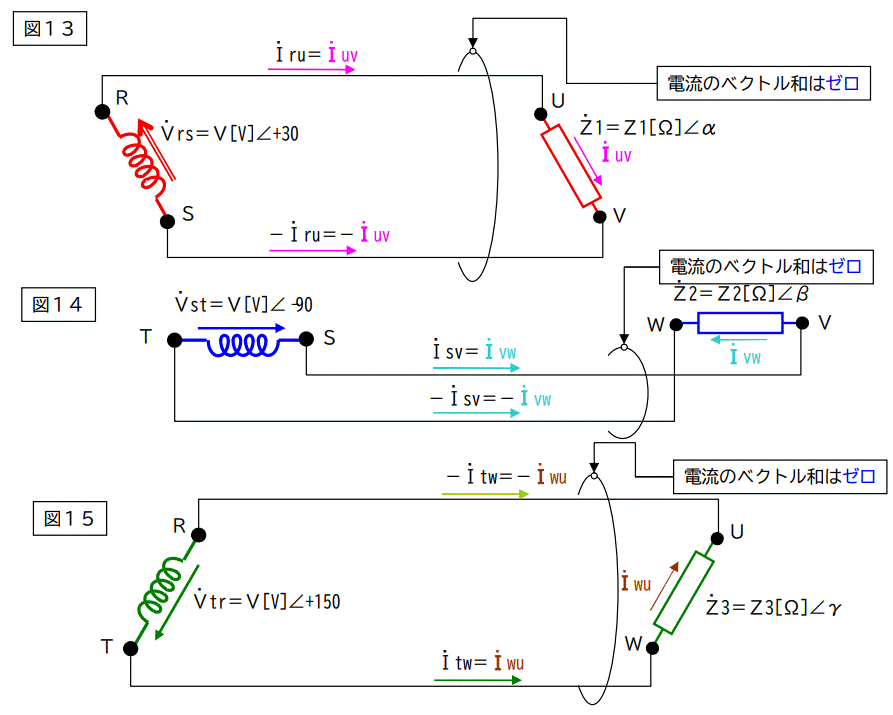
計算するまでも無く、これらの回路の電流のベクトル和はゼロです。
従って元の回路の電流のベクトル和はゼロになります。
今度はスターの場合です。
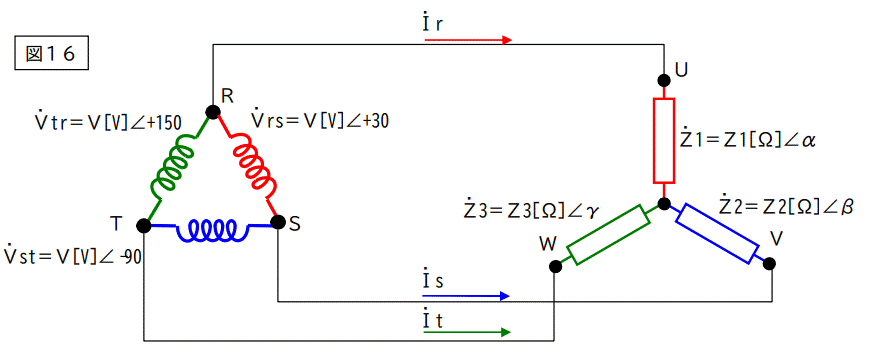
この負荷をデルタに変換します。
スターデルタ変換の公式を使います。
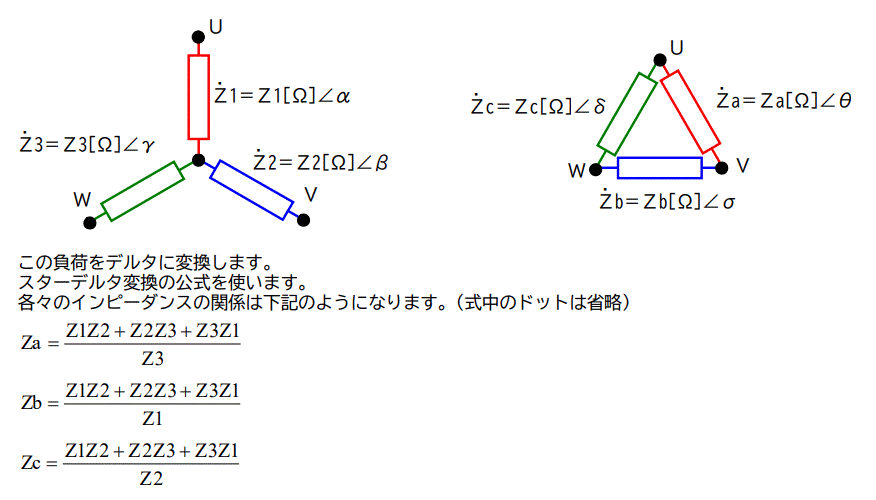
これらの変換結果を図12に展開すれば、デルタ回路の場合と全く同じ結果が得られます。
従って、スターの場合も電流のベクトル和はゼロになります。
デルタの場合もスターの場合も、インピーダンスの絶対値及び位相角に制限は有りません。
どの様なインピーダンスでも構わないワケです。
ですから、三相電源に、三相負荷と単相負荷を不平衡に接続した場合なども網羅されます。
一般的に電源は平衡電源と見なせる場合が殆どですが、負荷は日常的に不平衡になります。
ですから、負荷が不平衡になった場合、どの様な電流が流れるかを把握しておけば十分です。
対称座標法???ノーサンキューです。
普通のキルヒホッフの定理を用いた計算で十分です。
コメント