皆様 こん○○は
今回の御題は「対称座標法」です。この解析手法を解説したものは沢山有りますが、「ヨクワカラン!」というものが多いと思います。そこで毎度の事ですが「骨流トンデモ解説擬き」を作りました。この記載が何かの参考になる事を期待します。

平成 鹿年 骨月 吉日
サイタマ・ドズニーランド・大学 SDU 学長 鹿の骨 記
一説に依ると SDU はさいたまドスケベ大学ではないか?と言う話が有るが、あながち間違いでは無い。
超入門 対称座標法
早速ですが下図をご覧ください。
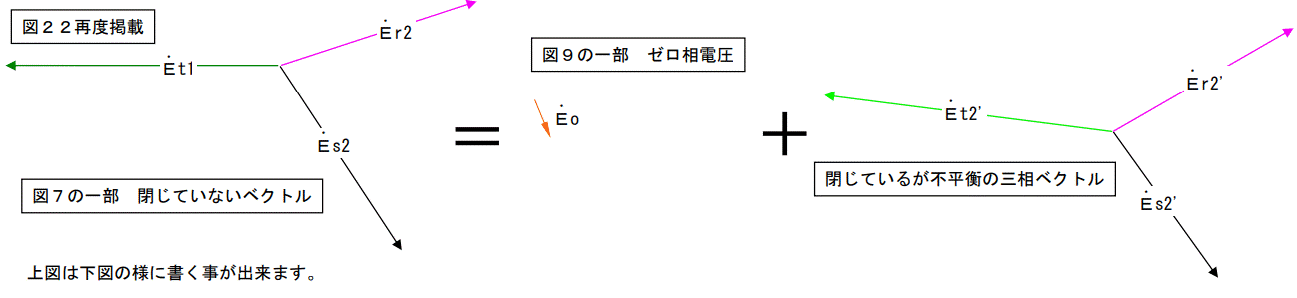
図1は不平衡で且つ閉じない三相電圧のベクトル図です。
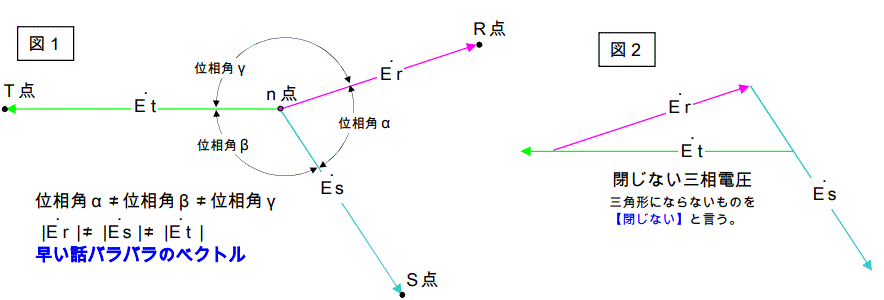
n点は中性点のつもりで書いていますが、図2を見ると解るとおり、この三相電圧は閉じていません。
つまりn点は中性点ではありません。中性点を探してみましょう。
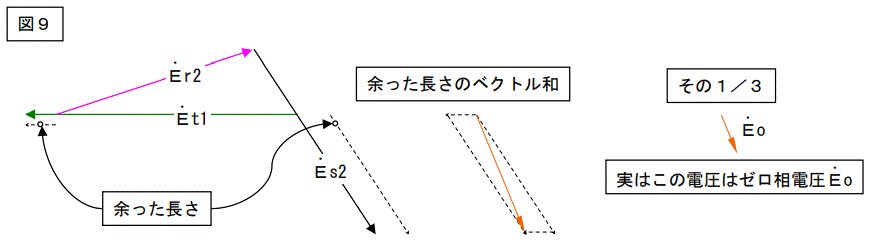
まず図3の様に余った長さのベクトル和の1/3を作ります。
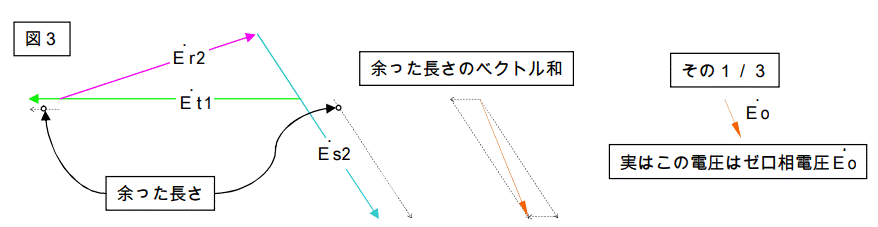
その1/3を使って図1を変形すると下図が書けます。
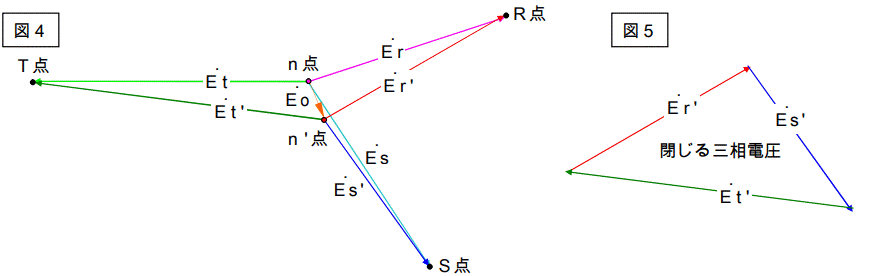
図5を見ると解りますがこの三相電圧は閉じます。
つまりn’点は中性点です。Eo を【ゼロ相電圧】と言いますが、此処ではフーンという程度で結構です。
何で1/3やねん?==>次項を読め
図4がなぜそうなるのかと言う説明です。
もう少し先へ行きます。
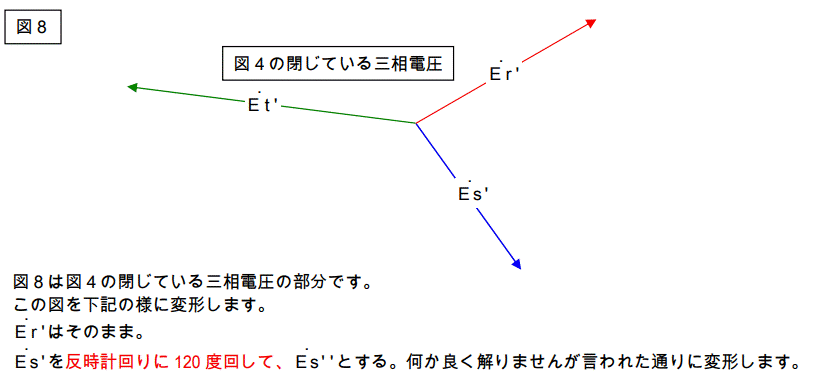
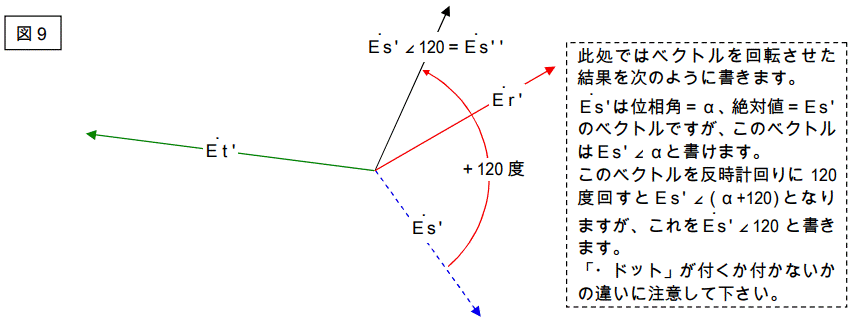
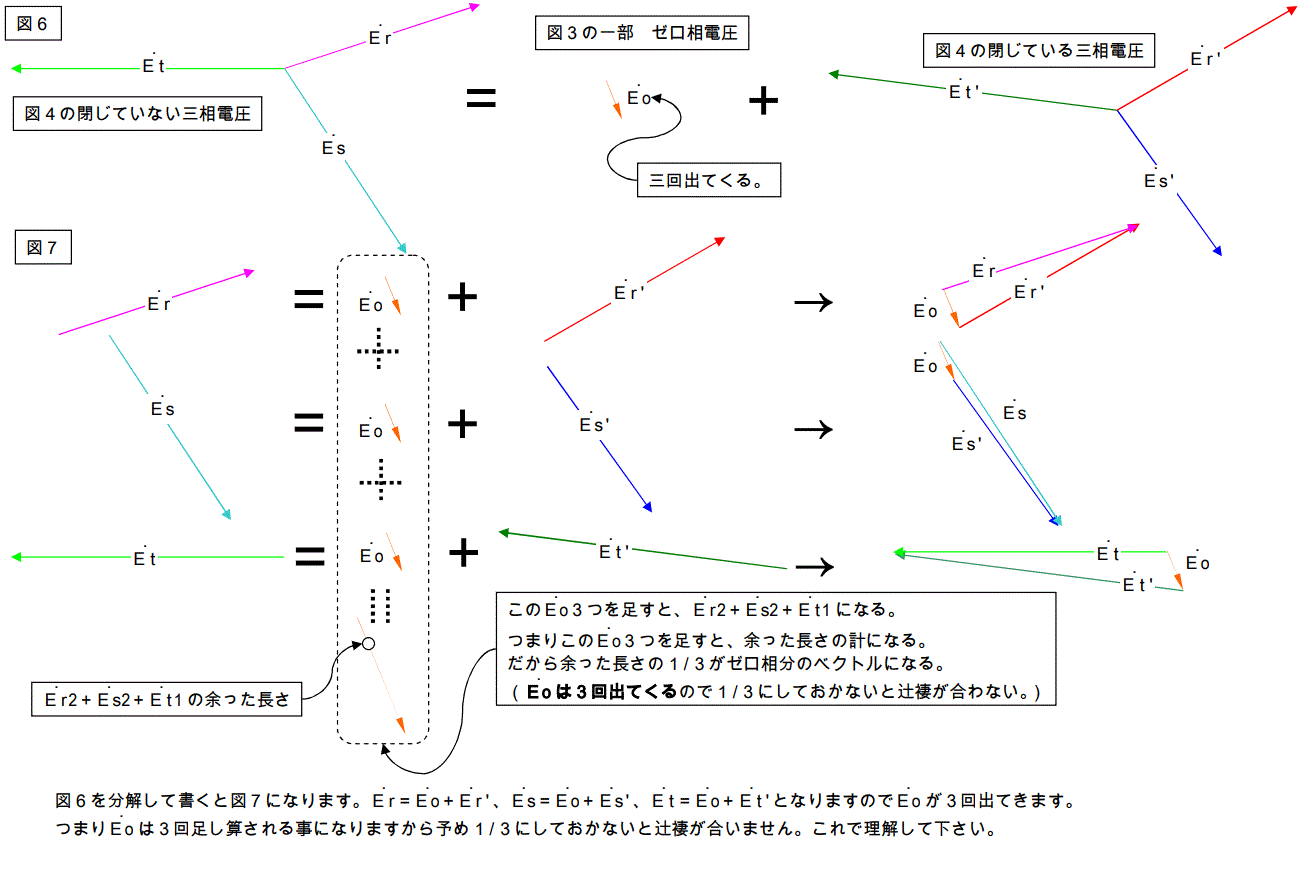
さらにこのベクトルをこねくりまわします。
この先、暫くは「ワケワカメ!」の記述が続きます。辛抱して読んで下さい。
図10を下記の様に変形します。
単純に3つのベクトルを足し算しろ。 → 図11
その1/3を作ってE1 としろ。 → 図12
その1/3と
それを時計回りに 120 度回したもの
及び時計回りに 240 度回したものを作れ。 → 図13
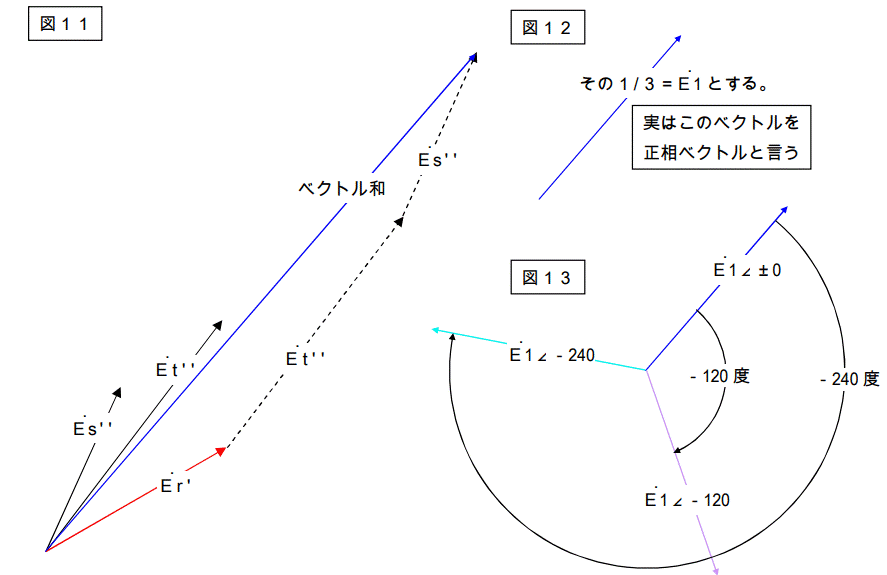
何が何だかサッパリ解りませんが図13が出来ました。
これはこれでひとまず置いて、今度は図8を次のように変形します。
Er’はそのまま。
Et’を反時計回りに 120 度回してEt2”’とする。
今回も何か良く解りませんが言われた通りに変形します。
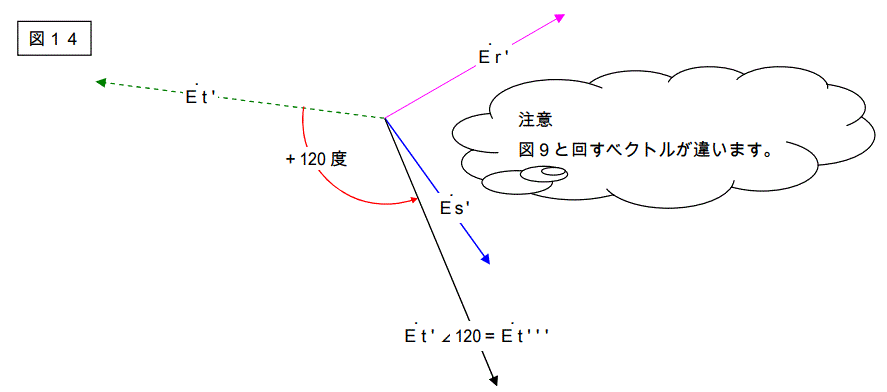
さらに次のように変形します。
Es’を反時計回りに 240 度回して、Es”’とする。
結果は下記になります。
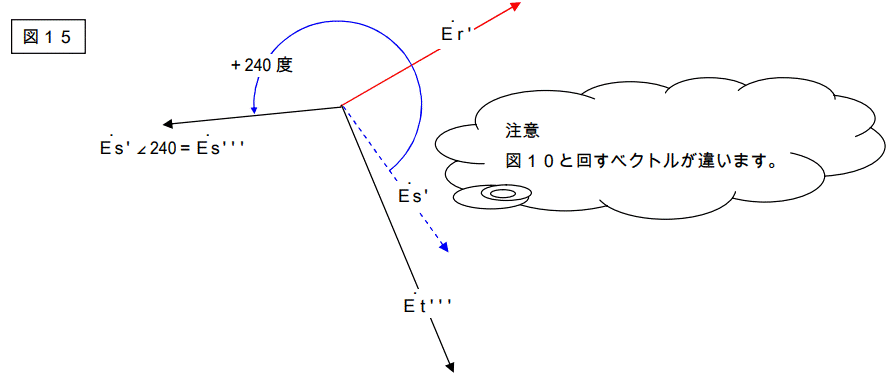
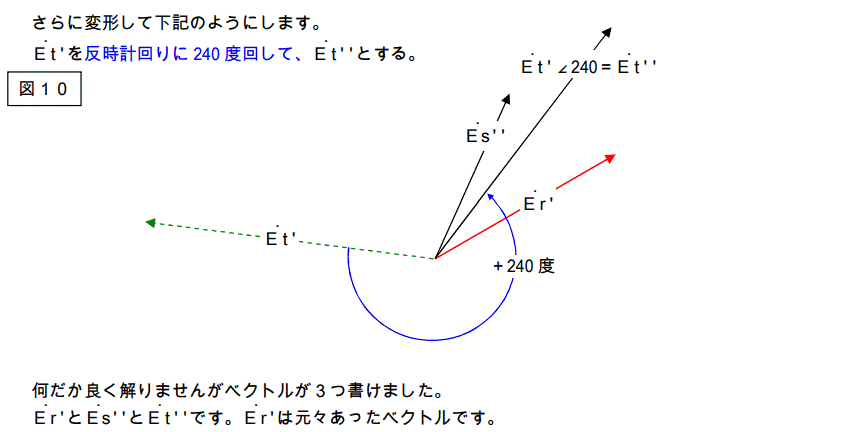
図15を下記の様に変形します。
単純に3つのベクトルを足し算しろ。 → 図16
その1/3を作ってE2 としろ。 → 図17
その1/3と
それを反時計回りに 120 度回したもの
及び反時計回りに 240 度回したものを作れ。 → 図18
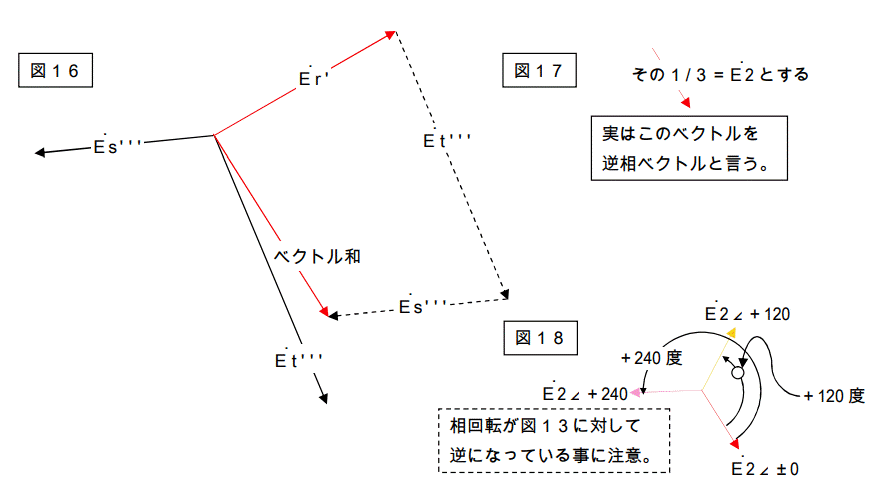
何やら訳もわからずに図18が出来ました。
これをどうしようと言うのでしょうか?
続きます。
今度は図13と図18と図8を持ってきます。
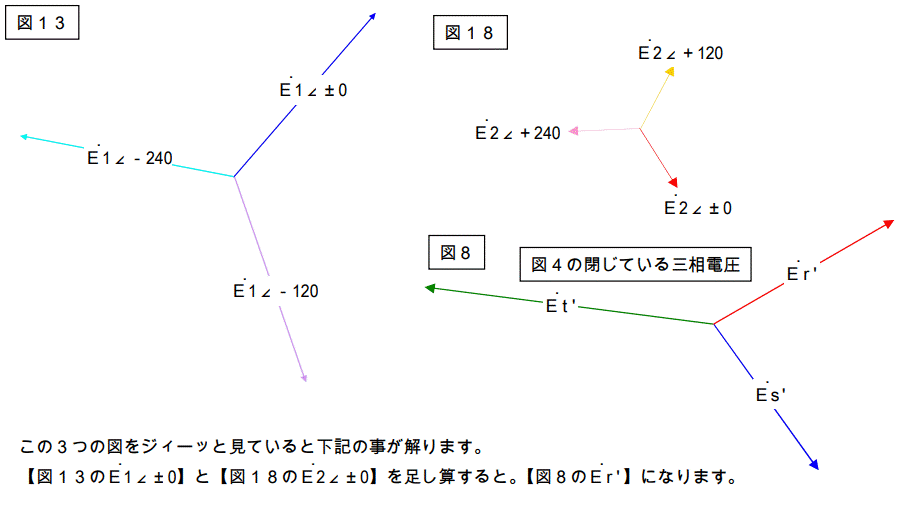
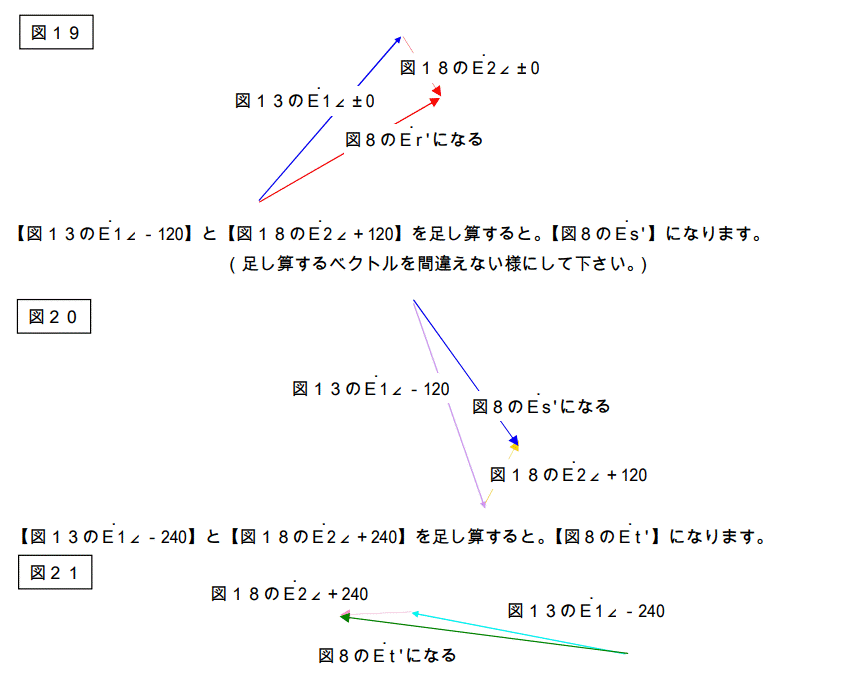
何やねん?これは?・・・不思議でしょぉ~・・・
もうアタマの中はグルングルン・・・次ページで少し整理します。
整理して関係式で示すと下図になります。
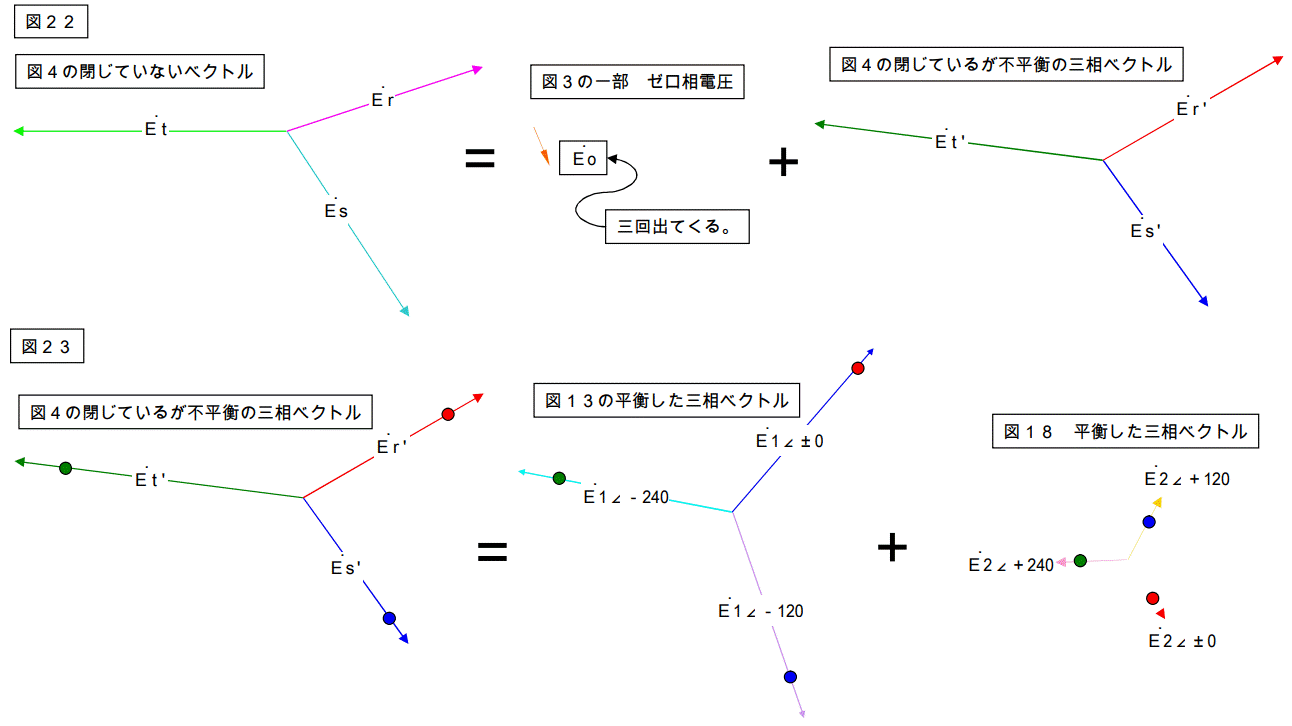
この様にバラバラな三相ベクトルは単相ベクトル+正回転の平衡三相ベクトル+逆回転の平衡三相ベクトルに分解することが出来ます。
(●●●は各々足し算するベクトルを示します。どのベクトルとどのベクトルの和を取るのかよく見て下さい。)
これが対称座標法の原理です。次ページでどうしてこの様な事になるのかの証明をします
何故この様な事になるのか証明して見ましょう。
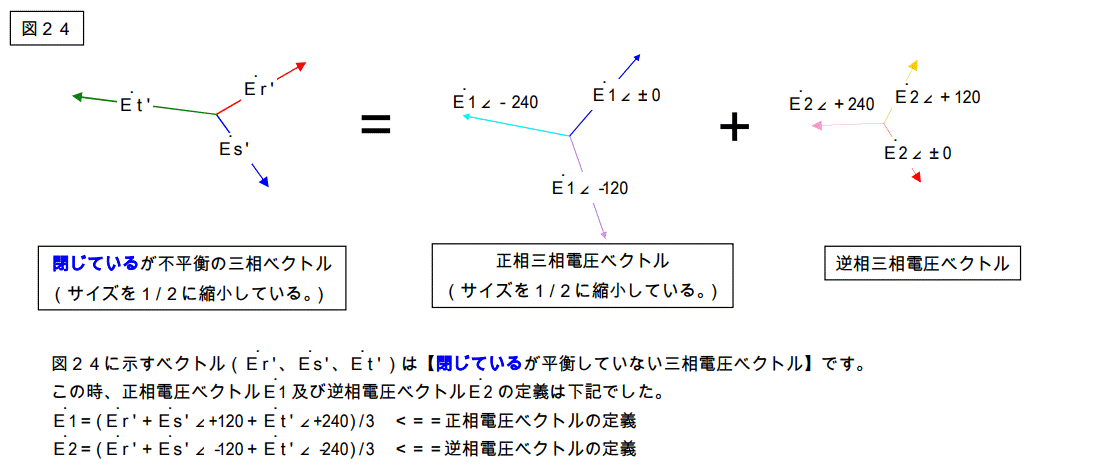


と言う結果が得られますので無事証明されました。
この様に図 24 に示された通り、閉じている不平衡な三相ベクトルは、
相回転が正方向の平衡三相ベクトルと逆回転の平衡三相ベクトルの和として表す事が可能です。
また7ページ図 22 に示した通り、完全にバラバラな三相ベクトルは単相ベクトルと閉じる三相ベクトルの和として計算が可能です。
結果として、完全にバラバラな三相ベクトルは
単相ベクトル+相回転が正方向の三相平衡ベクトル+相回転が逆の三相平衡ベクトルの和として計算できます。
もう少し書きます。

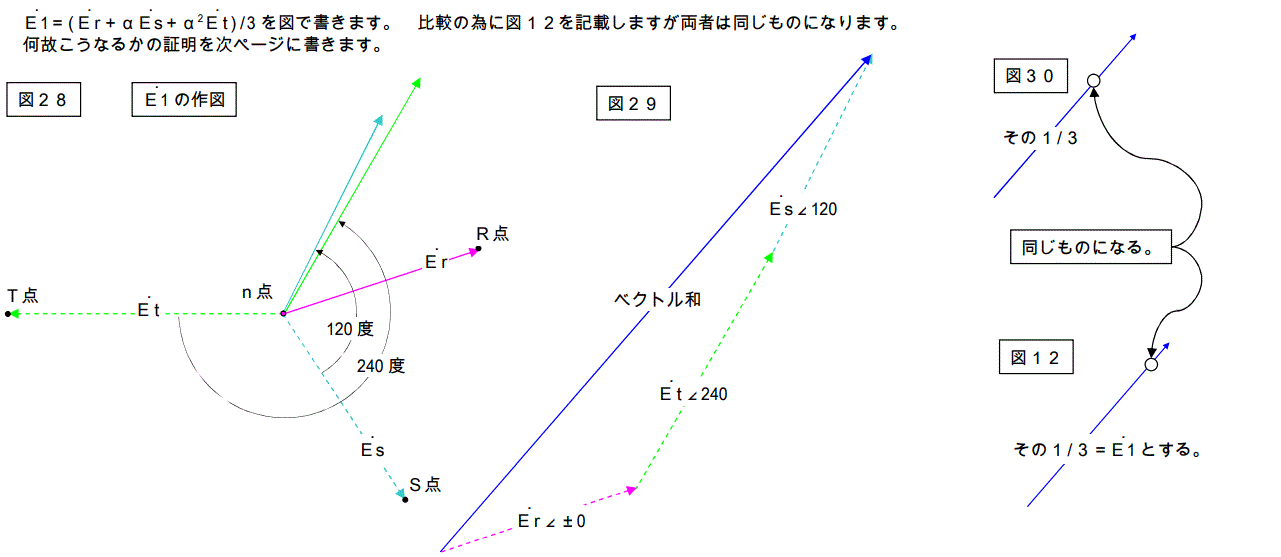
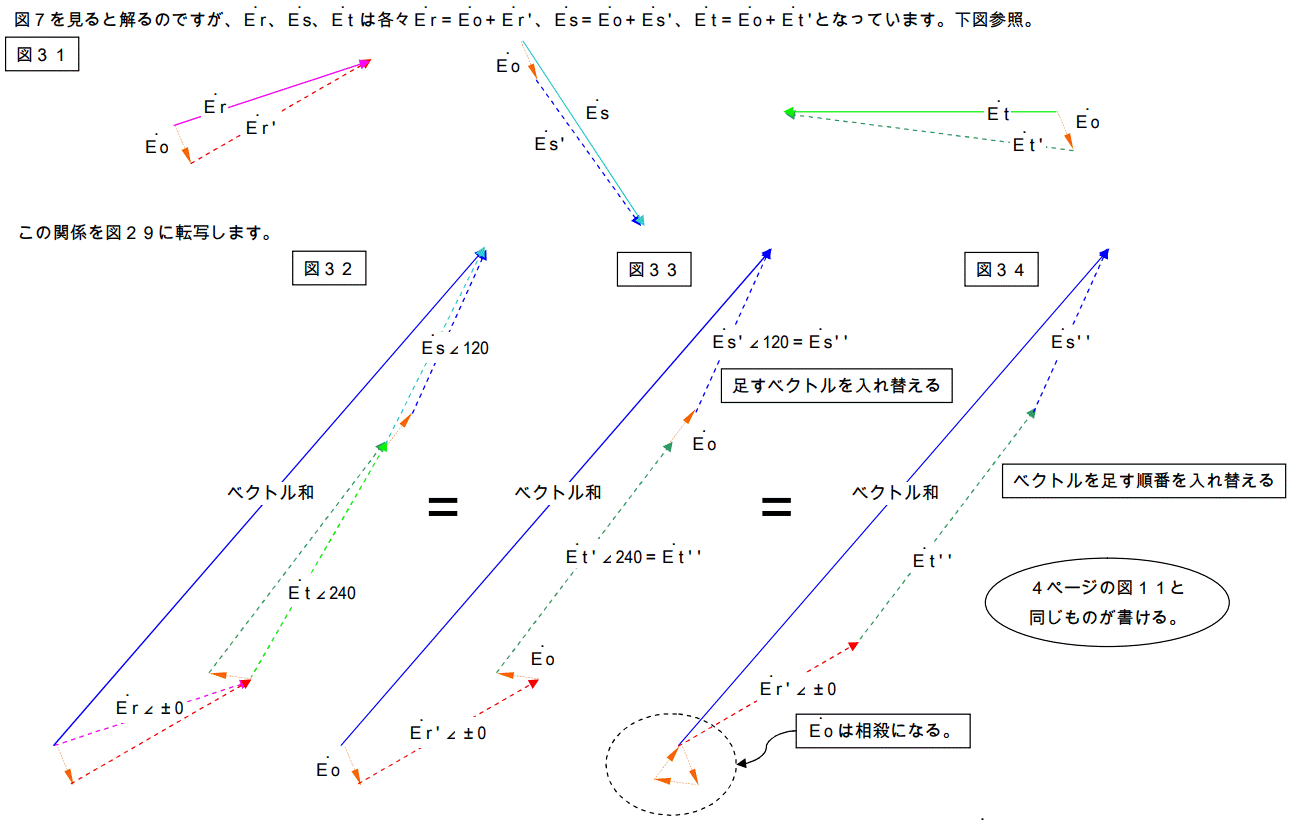
この様に図29でかいたベクトル和は図11で書いたベクトル和と同じものを書いている事が解ります。結果としてE1 は同じものになります。
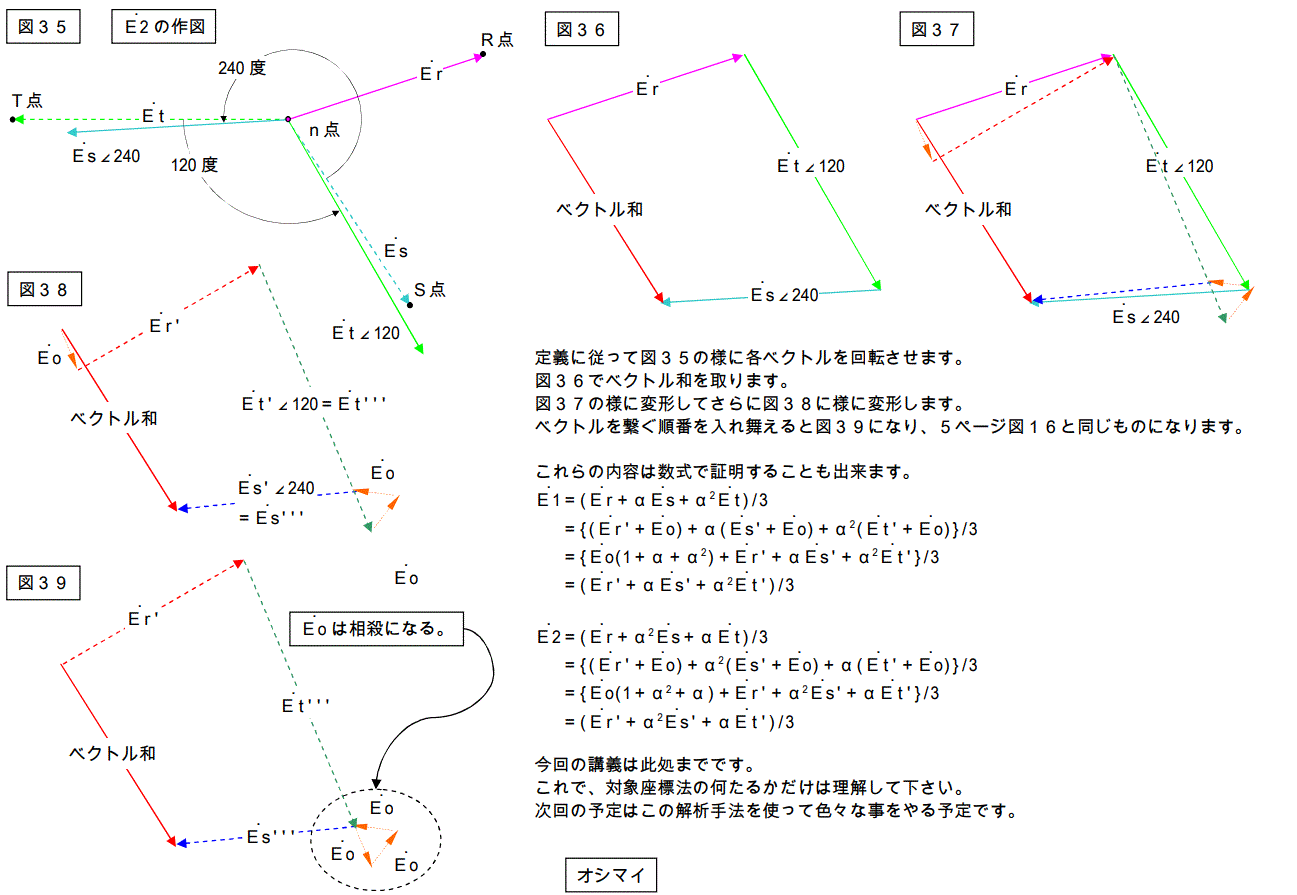
E2 の場合を次ページに記載します。
超入門 対称座標法2
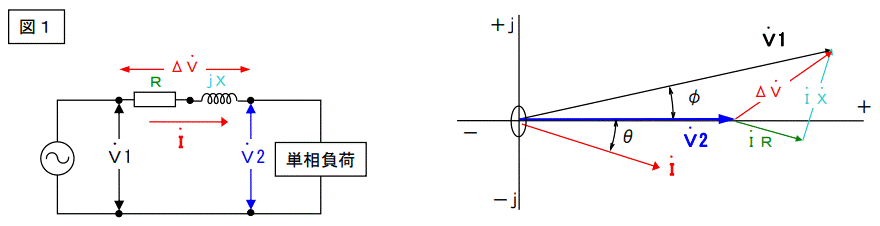
早速ですが、下図をご覧ください。
普通にある回路図とベクトル図です。この回路図とベクトル図は電圧降下の説明などに良く使用されます。
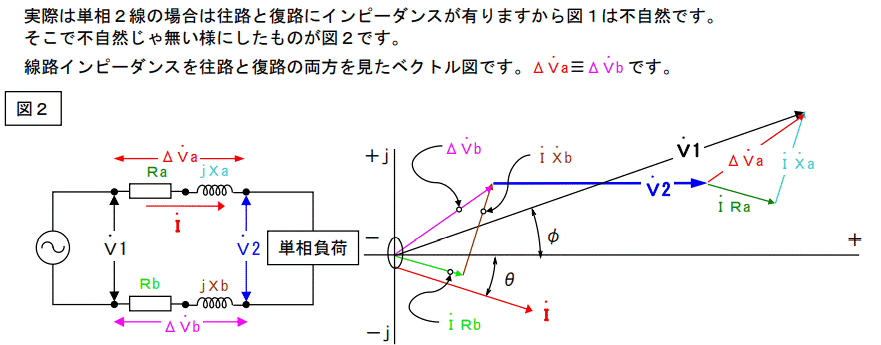
単相回路と言っても元々は三相だから、この回路を三相電圧電源の片相に繋ぐと下図になります。
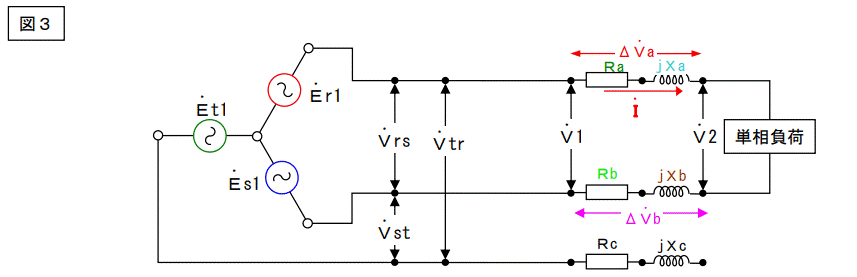
この回路のベクトル図を次ページに示します。
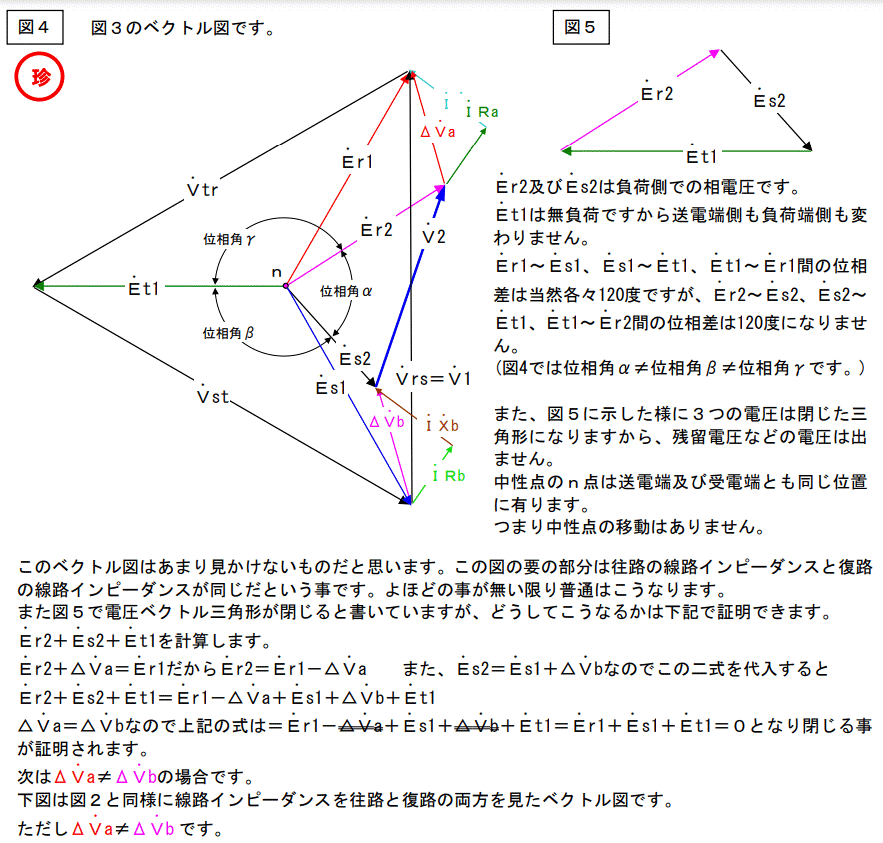
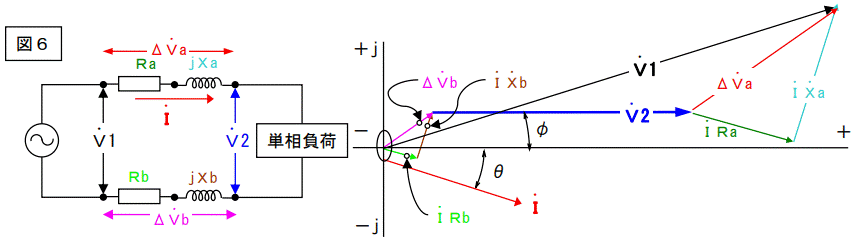
往路のインピーダンスが復路のインピーダンスより小さい場合を書いています。一般的にこの様に極端に不揃いになる事は無いのですが、なったらという事で書きました。この場合の三相ベクトル図を次ページに示します。
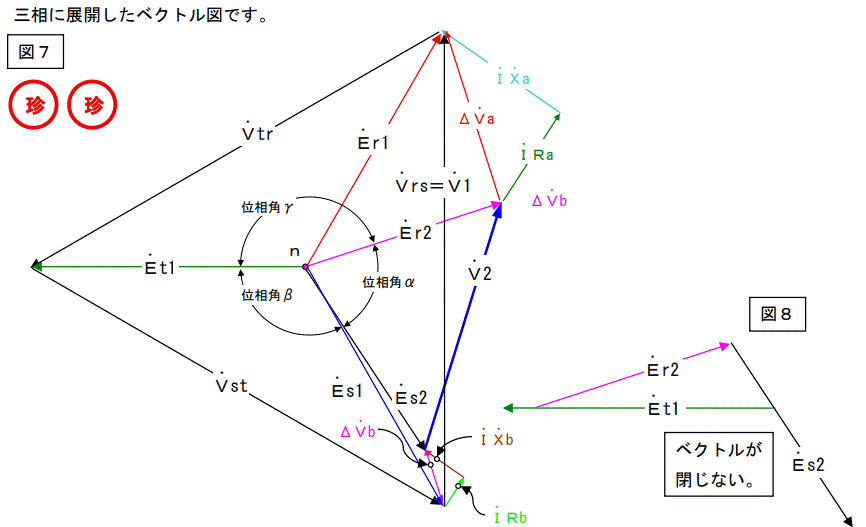
図8は負荷端電圧ベクトルの相電圧を重ねたものです。
見れば解るとおりこの三角形は閉じていません。
どうやら図7は間違っているようです。
送電端側の中性点nと負荷端側の中性点nが同じとしている所が間違っています。負荷端側の中性点はn点では無いようです。
これをこんな感じで説明を書きます。
図8を変形します。
いきなり【対称座標法】の用語のゼロ相電圧が出てきました。
此処ではこの単語に余り惑わされない様にして下さい。
兎に角、余った電圧のベクトル和の1/3のベクトルを作って見たと言う感じで結構です。
図9で作った【その1/3】を使って図7を変形すると下図が書けます。
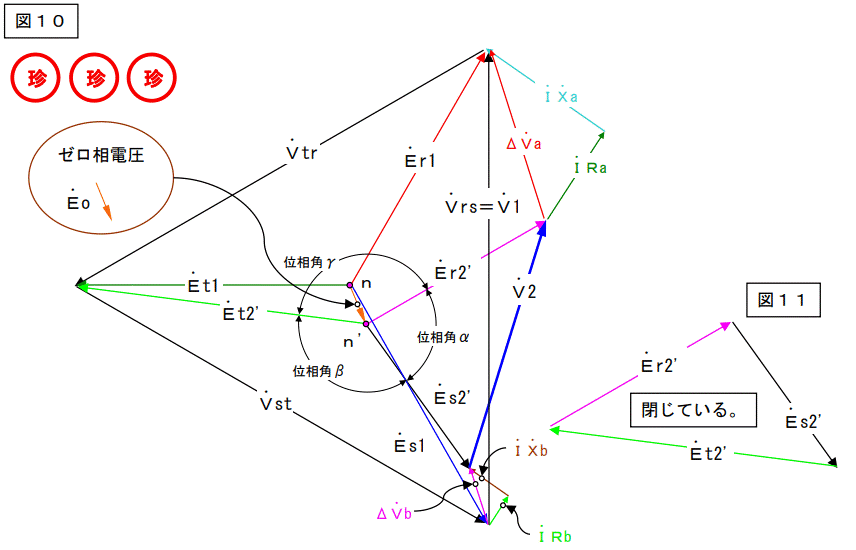
図11は負荷端電圧ベクトルの相電圧を重ねたものです。
見れば解るとおりこの三角形は閉じています。
図7と図10を比較すると、図10は負荷端の中性点がn’の位置に動いています。
(【その1/3】の長さだけ動きます。)
この移動した距離、n~n’間の電圧を【対称座標法のゼロ相電圧】と言います。
一般的にゼロ相電圧は地絡を伴って出現すると思われていますが、この様に配電線の回路定数の不平衡と負荷の不平衡に依っても起きる事が解ります。
此処でもう少し対称座標法の勉強をしてみましょう。
図11を変形します。図12とします。
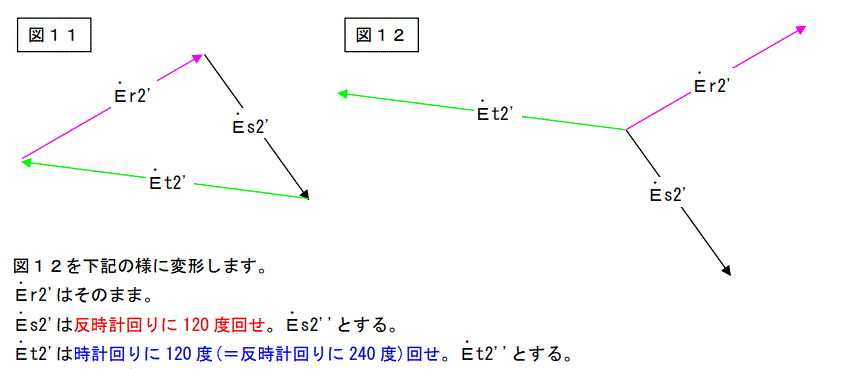
図12を下記の様に変形します。
Er2’はそのまま。
Es2’は反時計回りに 120 度回せ。Es2”とする。
Et2’は時計回りに 120 度(=反時計回りに 240 度)回せ。Et2”とする。
結果を次ページに示します。
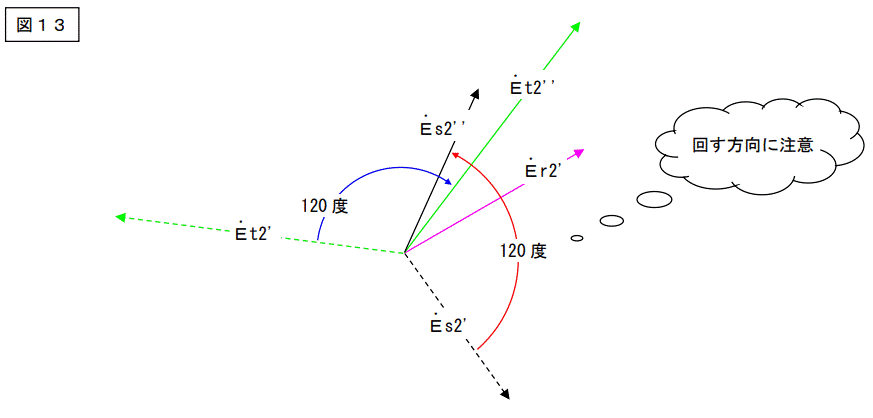
図13を下記の様に変形します。
単純に3つのベクトルを足し算しろ。 → 図14
その1/3を作れ。
その1/3と
それを 120 度回したもの
及び 240 度回したものを作れ。 → 図15
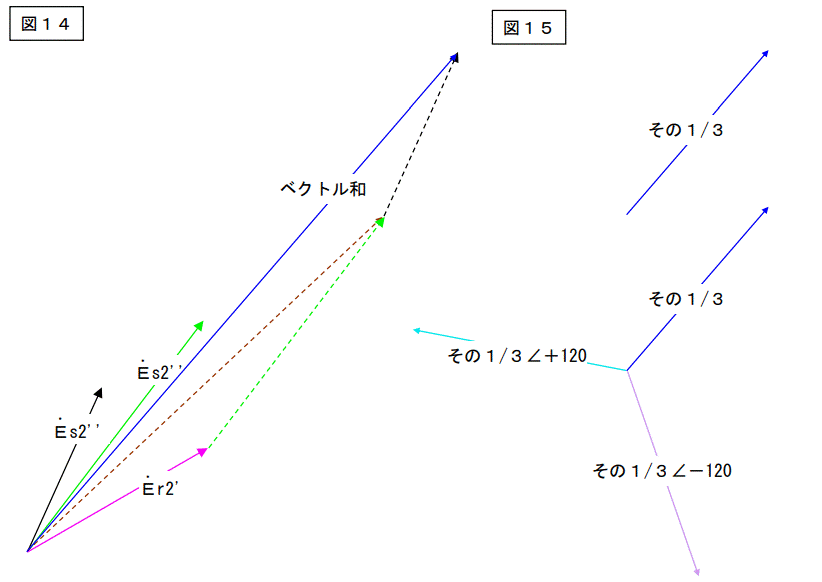
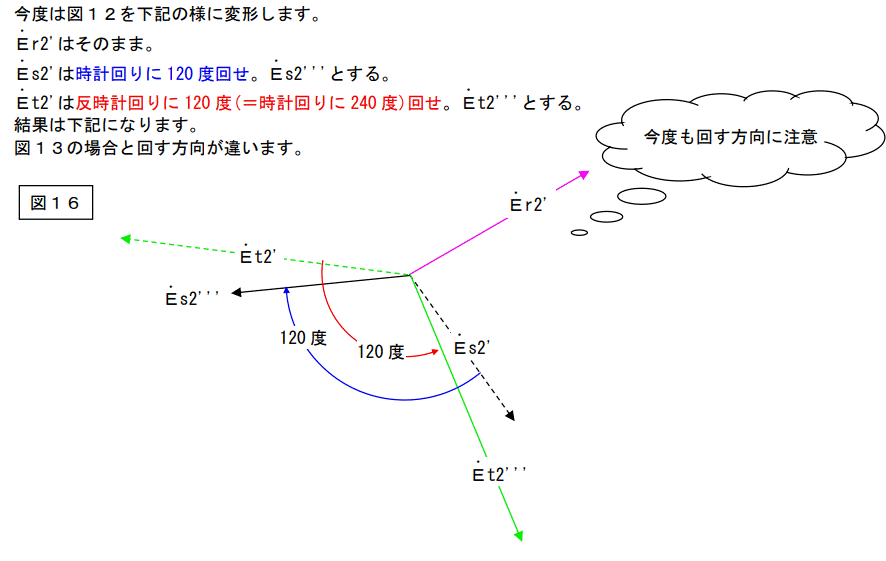
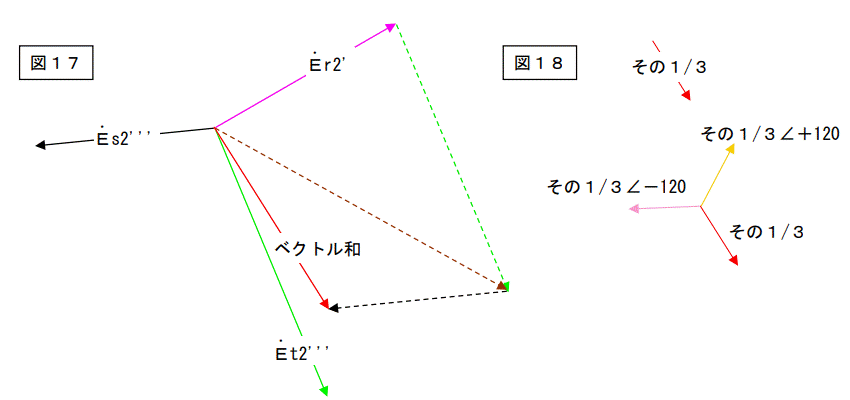
図16を下記の様に変形します。
単純に3つのベクトルを足し算しろ。 → 図17
その1/3を作れ。
その1/3と
それを 120 度回したもの
及び 240 度回したものを作れ。 → 図18
今度は図15と図18を持ってきて下記の様に変形します。
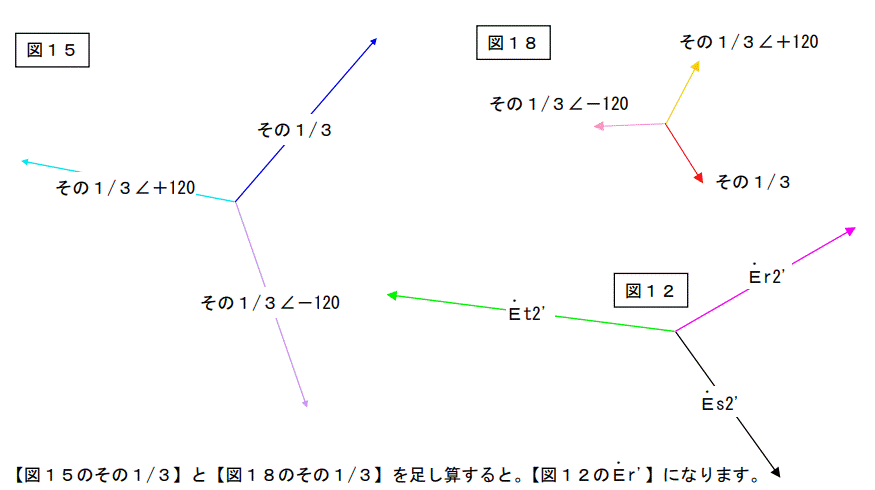
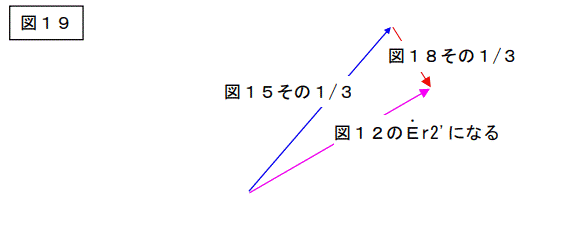
【図15のその1/3∠-120】と【図18のその1/3∠+120】を足し算すると。【図12のEs’】になります。(足し算するベクトルを間違えない様にして下さい。)
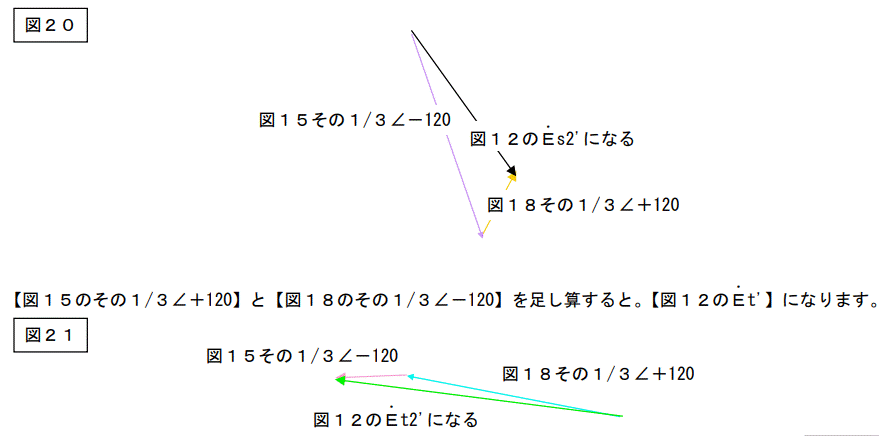
整理して関係式で示すと下図になります。
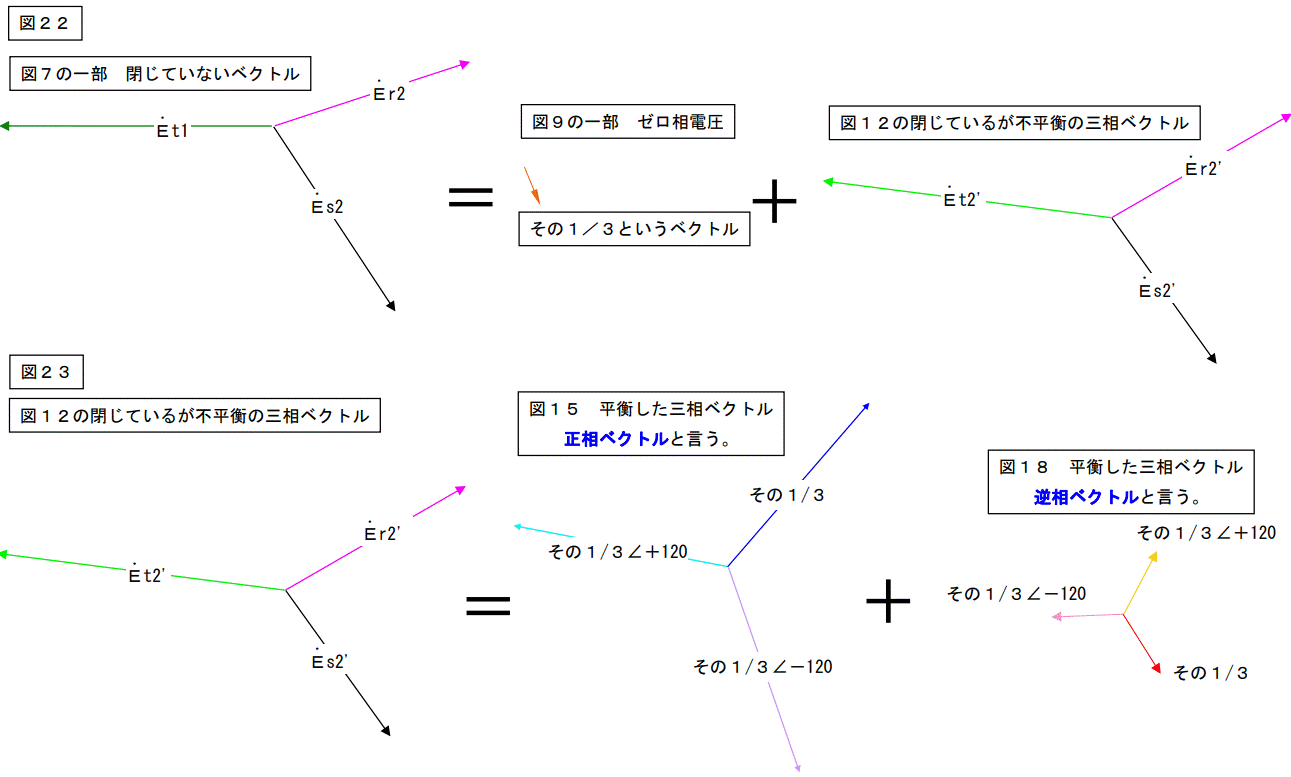
この様にバラバラな三相ベクトルは単相ベクトル+正回転の平衡三相ベクトル+逆回転の平衡三相ベクトルに分解することが出来ます。これが対称座標法の原理です。
何故この様な事になるのか証明して見ましょう。
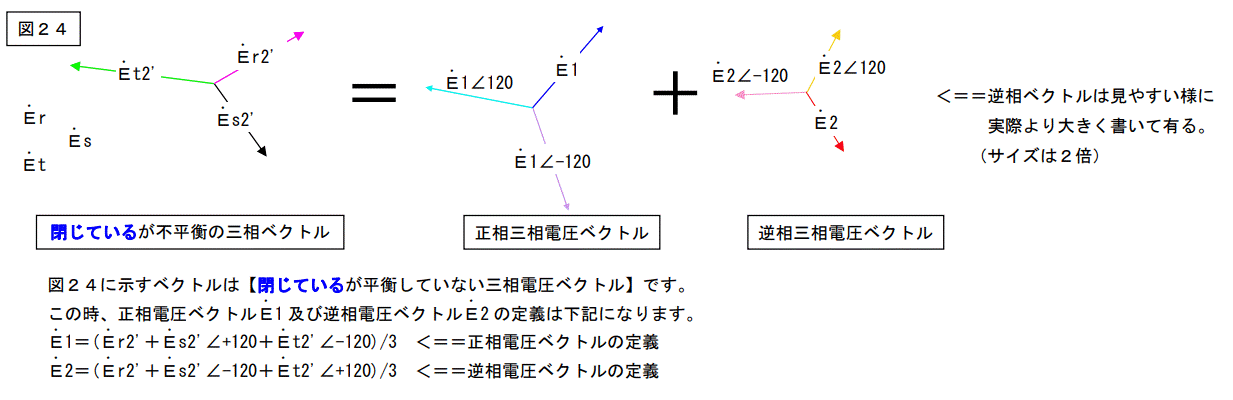
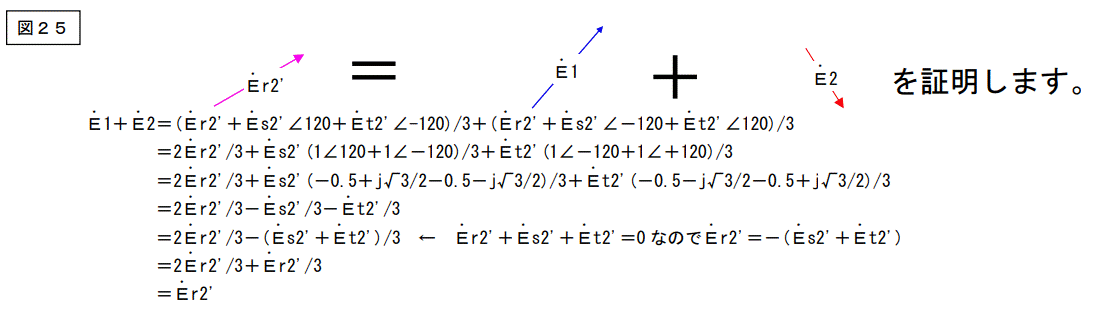
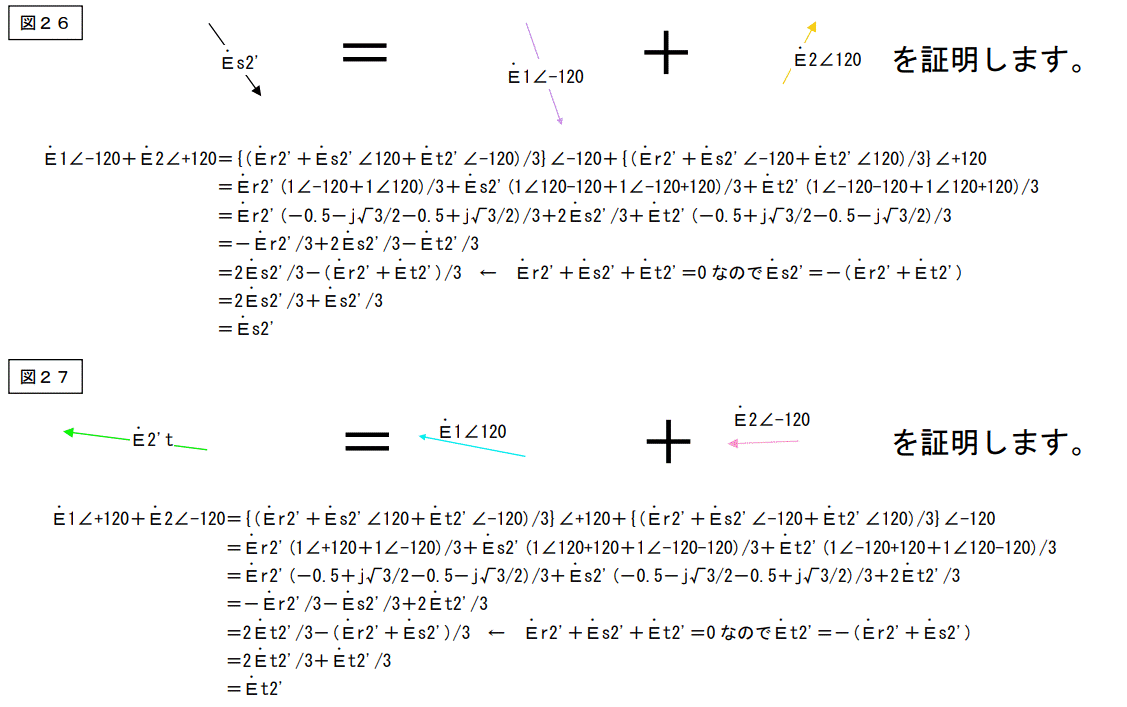
と言う結果が得られますので無事証明されました。
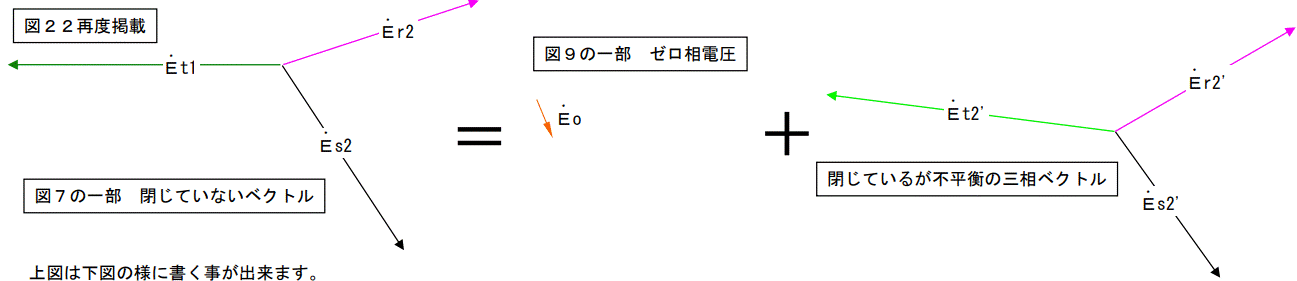
次は【閉じていない三相電圧ベクトル】の場合です。
【閉じていない三相電圧ベクトル】=【ゼロ相電圧ベクトル】+【閉じているが平衡していない三相電圧ベクトル】
となる事の証明です。
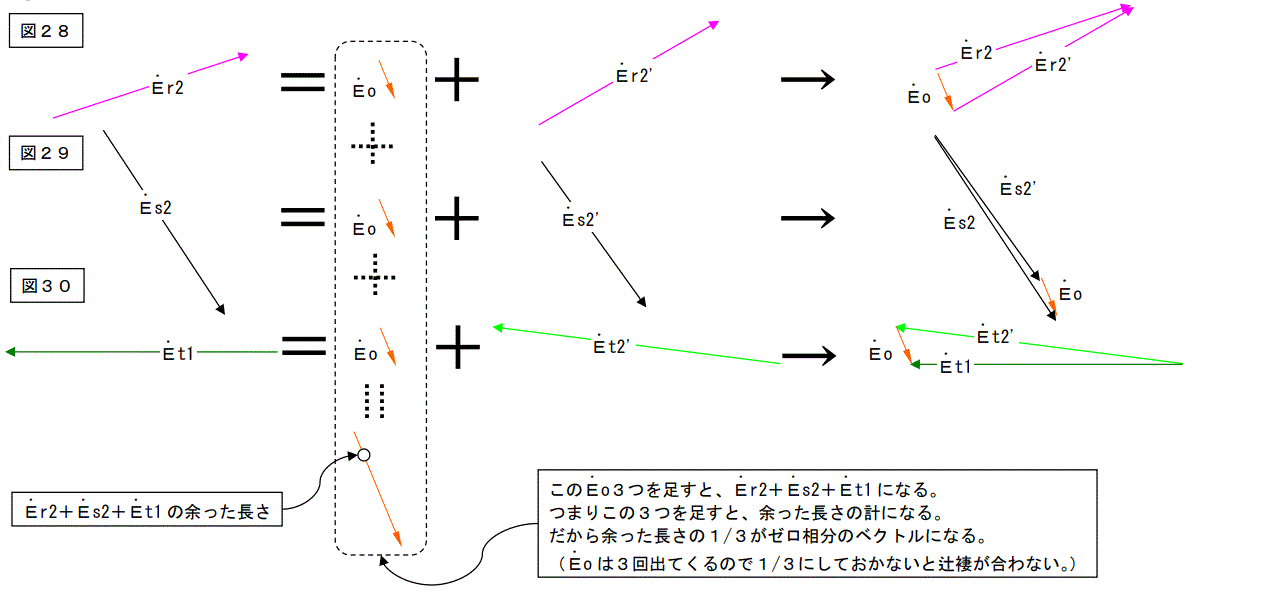
コメント