虚数【j】を使った計算のからくり

普段当たり前の様に使用している虚数【j】であるが、これを使って回路計算を行ってみよう。
例えば下図の様な問題があったとする。この回路に流れる電流は下記の様に計算すれば簡単に求める事が出来る。
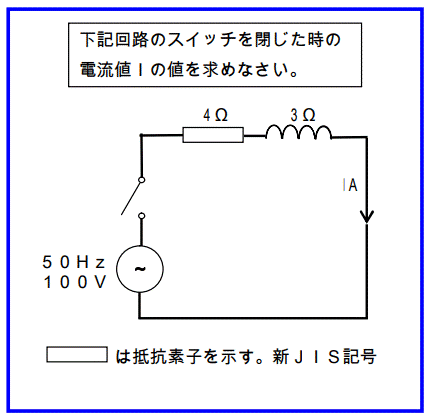
電流を求める方程式は下記のようになる。

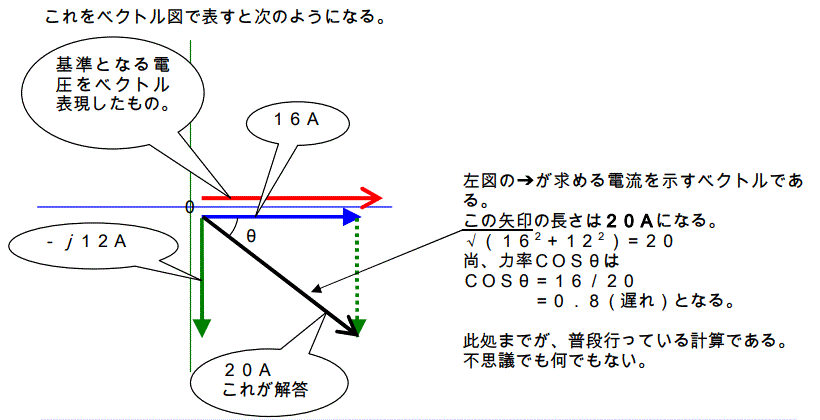
ここで新たに問題提起をします。
何故この様な計算で良いのかを証明しなさい。
jという訳のワカラン記号を使った計算が何故正しいの?
おかしいじゃん?ワケワカンナイ?
ウッ!・・・次ページを参照されたし・・・。
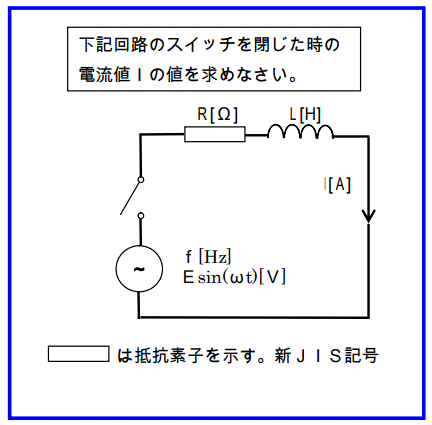
前項と同類の問題である。
数値が全て一般値で与えられているのが前ページとの違い。
学術的に左記の問題を解析すると次のようになる。
●電圧
周波数はf[Hz]とする。
電源は交流電源であるから、SIN 関数になる。
(COS 関数でも良い。)
波高値はEとする。
●抵抗素子
R[Ω]と置いただけ。
前ページと変わりは無い。
●インダクタンス素子
単位が[Ω]では無く。[H:ヘンリー]で書いてある。
ナンジャコリャ?
余り深く考えないで、インダクタンスの由緒正しき単位はオームでは無くてヘンリーと言う位に思って
先に進め。
●電圧と電流及び各素子の関係式
電源電圧と電流及び各素子の関係式は下記の方程式になる。
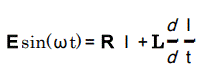
ナンジャコリャの100倍?
いきなり訳の解らない方程式が出現した。
微分の要素を含んでいるので「微分方程式」と呼ばれる方程式である。
この方程式を解いて、電流Iを時間tの関数で示せ、と言うのである。
上記の式でωは下記の数式で示される定数である。(角速度と言う。)
ω=2πf
又、ω以外の定数(前もって解っている変化しない値)は下記である。
E:波高値
f:周波数
R:抵抗値
L:インダクタンス値
この方程式を解け! と言われてもどこから手を付けたら良いのか見当が付かない。
参考書を買って、それを見ながら解くことにする。
参考にした参考書は下記
書籍名:工学系学生のための 記号法ですぐに解ける微分方程式
著者 :金田 数正
発行所:(株)内田老鶴圃(ウチダロウカクホ <==変な名前?)
価格 :1800円+税
次ページに実際に解いた結果を示す。
(微分方程式を解くのはかなり厄介である。)
与えられた微分方程式は下記であった。
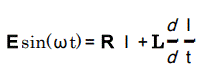
三角関数を用いて無理矢理解く方法もあるらしいが、此処では参考書に従い、「記号法」とやらを用いて解いてみる事にする。

手順その6
If=C1ehtと書け!
C1は任意の定数である。
もう頭の中はグルングルン
h=-R/Lだから、
If=C1e(-R/L)t
(e は2.718281828・・・で示されるまか不思議な数値であり、自然対数の底である。)
これで何が求められたの?
微分方程式の基本解が求められた。
因みに微分方程式の一般解は次の様になる。
一般解=基本解+特別解
つまり I=If+Ip である (IfはIの基本解、Ip はIの特別解を示す。)
益々訳がワカラン?
いいから次に進め。
特別解を求める。
ちょっとその前に・・・。
フランスの天才数学者のオイラーが導き出した指数関数と三角関数及び虚数を結びつける公式を紹介する。
ejα=COSα+jSINα
これは有名な式で、これが無かったら現在の電気工学は成り立たないと言われるほど重要な公式である。これを使って特別解を求めることにする。


従って次の手順は下記になる。
上記の式のDをjωに置き換えろ!
ギブアップ寸前です。



何が何だか訳のワカラン解が得られただけじゃん。
これじゃ余計に訳がワカラン。
と言っていないで次に進む。
上記の式を良く観察すると次のような事が解る。
右辺の第1項(基本解)に着目するとこの解は三角関数になっていない。
基本解=C1e(-R/L)tの部分である。
この部分はtの関数になっているが、tの値を色々と変えてみるとあることに気が付く。
tの値を充分に大きな値、つまりスイッチを入れてから充分に時間が経った場合を考えてみる。
どの位の時間を入れれば良いかは色々であるが、この際だから、無限大時間つまりt=∞としてみる。
基本解=C1e(-R/L)tのtを∞に置き換えると
=C1e(-R/L)∞となる。
これをもう少し解りやすく書くと下記になる。

見覚えのある式だ!!
この式は次のように読む。
この電流は、波高値がE/Zで電源電圧に対してθだけ位相が遅れたSIN関数である。
次に進め!
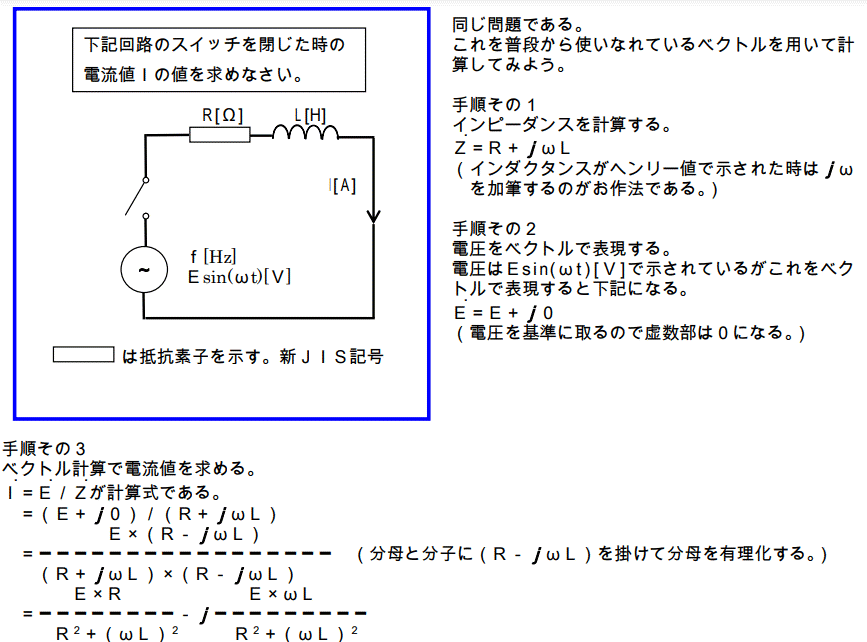
ここでtanθ=ωL/Rとなるような、θの値を定義すると、
SINθ=ωL/√{R2+(ωL)2}
COSθ=R/√{R2+(ωL)2}
Iを求める計算式を変形すると

前ページのベクトル式で示された式を再度示す。
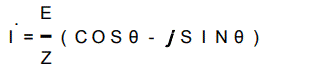
この式は何を示しているのであろうか?
この式から次の事が解る。
電流の大きさはE/Zである。
この電流の位相差は電源電圧に対してθだけ遅れている。
ここで微分方程式の場合の最終結論を再度記載する。
この電流は、波高値がE/Zで電源電圧に対してθだけ位相が遅れたSIN関数である。
これって同じ事を言っていないか?
もうお解りと思うが、これは全く同じ事を言っている。
つまり、下記のことが言える。
面倒くさい微分方程式を解かなくてもベクトル法を用いれば同じ結果が得られる。
これがjを用いた計算方法である。
もう少し記述を書く。
Eは本来であればESIN(ωt)で示されるSIN関数である。
ここでオイラーの公式をもう一度登場させると
ejα=COSα+jSINα
この式を適用して上記の式は次のように変形できる。
E=Eejωt(の虚数部。)
同様に

(三角関数の加法定理:SIN( α±β )=SINαCOSβ±COSαSINβを使用した。)
つまり微分方程式で得られた結果と全く同じ結果が得られる。
なにか騙された様で釈然としないが、この様な結果が得られる事は事実で有る。
取り敢えず此処まで。
さて続きの話である。
微分方程式の一般解をもう一度見る。

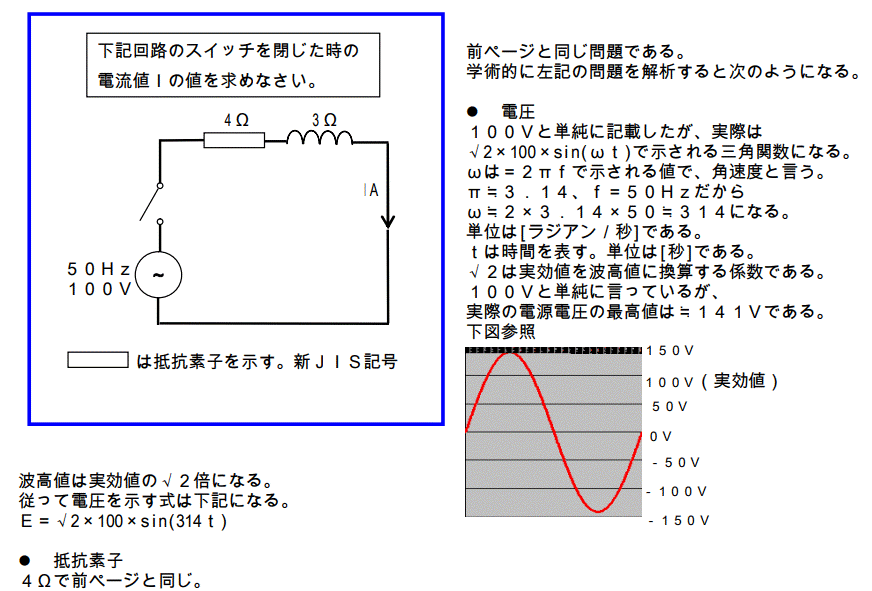
●インダクタンス素子
3Ωで前ページと同じ。<=ではない!!
素子の値がインピーダンスとしてオーム値で示された場合、実際のインダクタンスL[H:ヘンリー]とインピーダンスの関係式は下記になる。
Z=ωL
従って、L=Z/ω
≒3/314[H]

インダクタンスに対する電圧降下は流れる電流の変化量に比例することになっている。
従って、電流の時間に対する微分値に比例することになる。
とは言うものの、
こんなもの解けるか! になると思う。
この際だから、この微分方程式を解いて見る。
与えられた微分方程式は下記です。
(中卒及び高卒の方、申し訳ありません。これは大学で習う数学の範疇です。)


コメント