三相誘導電動機のスターデルタ始動時の電流について

三相の誘導電動機をスターデルタ始動した場合の電流の話です。
皆様ご承知の様に、スターデルタ始動はよく用いられる始動方法です。
この始動方式を用いた場合の、始動電流及び始動トルクの関係は次の様に説明されています。
説明その1
始動電流は全電圧始動の1/3になり、始動トルクは1/3になる。
説明その2
始動電流は全電圧始動の1/√3になり、始動トルクは1/3になる。
一つの事項に対する説明が2種類ある場合、次の事が言えます。
片方が間違っている。又は両方間違っている。
結論を先に書きます。
説明その1 <== 正しい。
説明その2 <== 間違い。
結構権威のある解説書などにも、この間違った記載があります。
何処でどう間違えたかは良く解りませんが、間違いは間違いです。
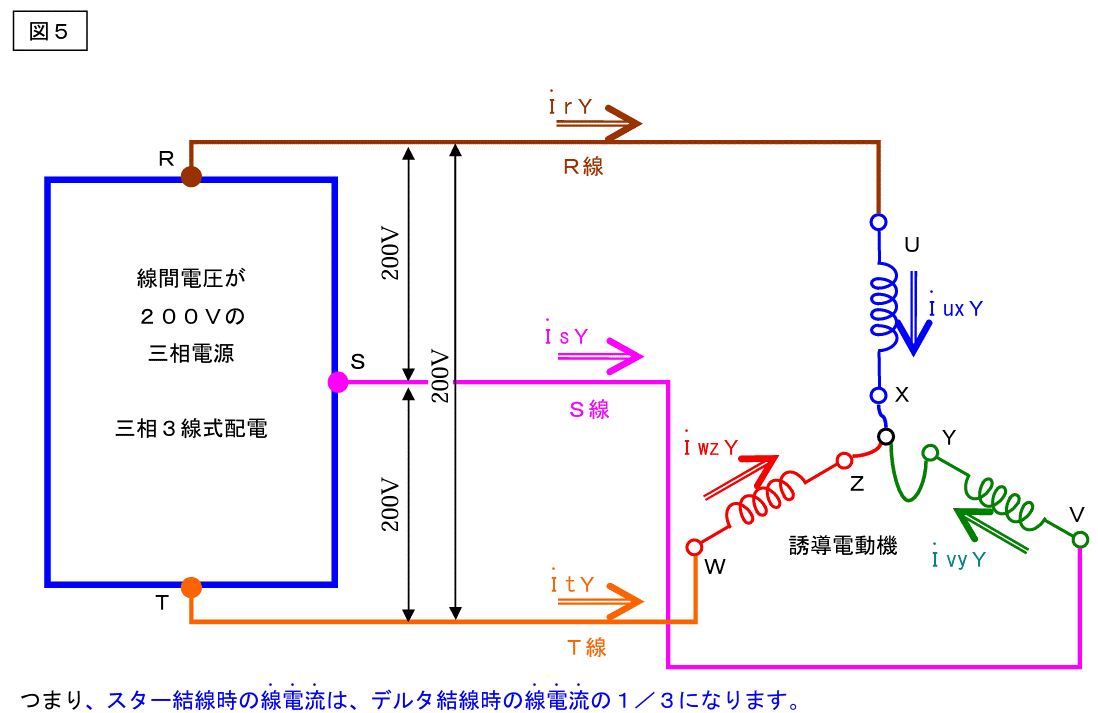
まず、基本回路ですが下図の様な回路で考えます。
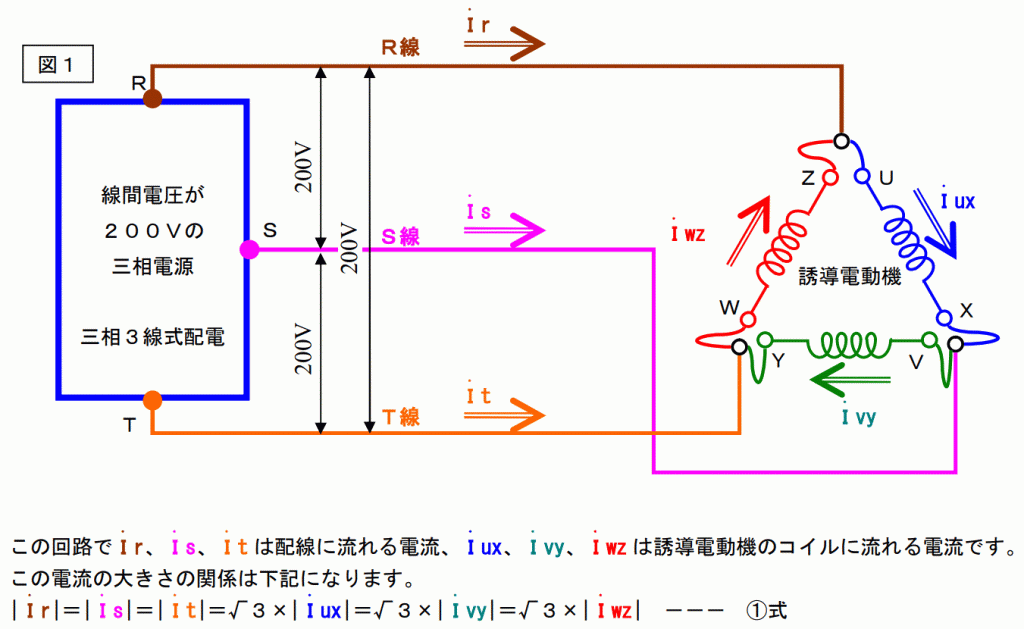
つまり、線電流は巻線電流の√3倍の電流が流れます。
ベクトル演算式は取り敢えず忘れて頂いて結構です。
電流値の大きさのみの比較です。
どうしてこうなるかは、「なるからなる。」としてください。
次に下記のような回路を考えます。
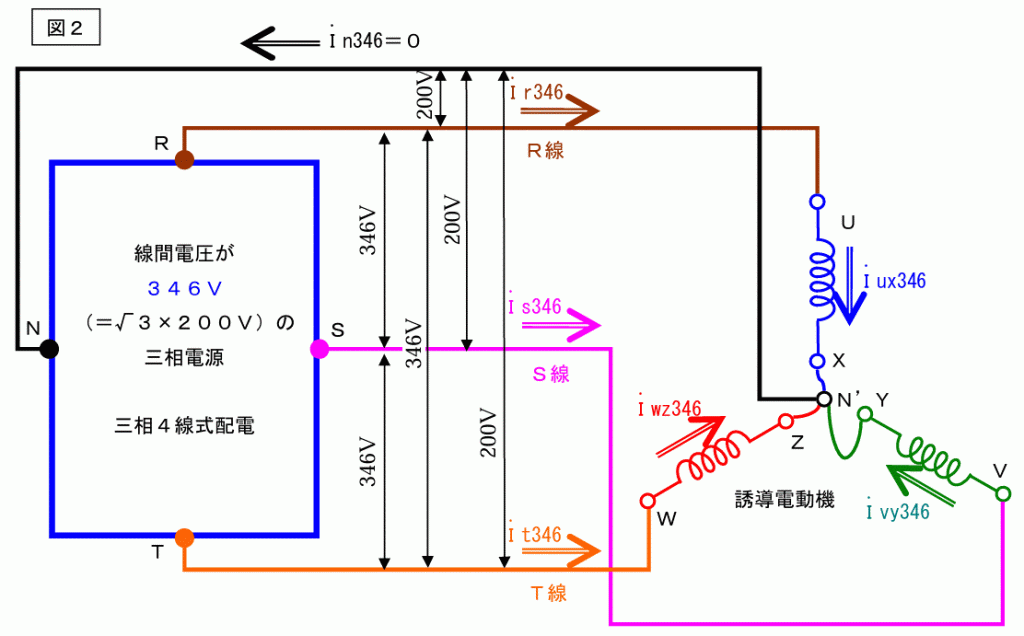
何やら奇怪な回路図ですが、この回路は、誘導電動機の巻線を△からYに組み直し、電源線間電圧を√3倍にしたものです。
N相の電流は0(ゼロ)になります。N線は有っても無くても同じですが、取り敢えず書いておきました。実際には線間電圧が346Vの電圧は商用電源には有りません。有りませんが、作ったらこうなるという事を考えます。
上図の場合、線電流と巻線電流は次の関係式になります。

ここで、2つの回路(図1及び図2)の電動機の出力を考えます。
コイルの組み方を変えて、線間電圧を変えた。
図1の場合の出力をP[kW]とすると、図2の出力は・・・次の内のどれか?
(1) P[kW]で同じ。
(2) √3×P[kW]になる。
(3) 3×P[kW]になる。
(4) P/√3[kW]になる。
(5) P/3[kW]になる。
正解は(1)です。
どうして、こうなるかを次項で説明します。
説明の為に次の様な回路を考えます。
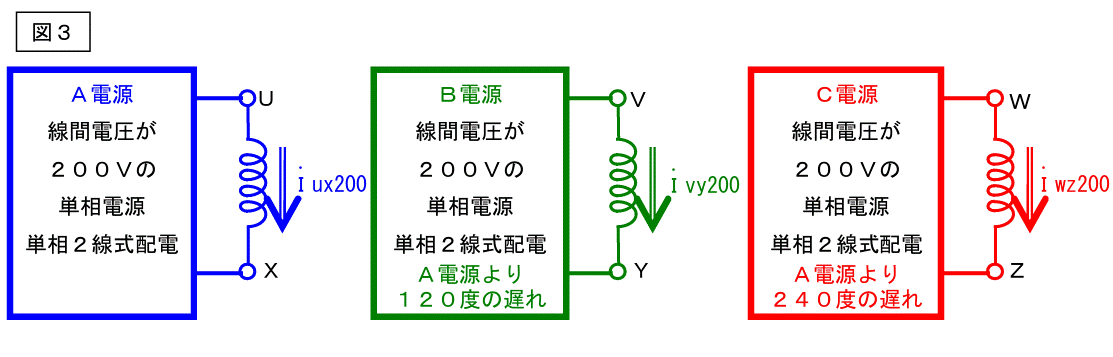
またまた、奇怪な回路図です。
この回路図は、誘導電動機の巻線をバラバラにして、各々に別々の単相電源を印加したものです。電源の電圧は全部同じで、200Vです。電圧位相はそれぞれ120度の位相です。つまり三相交流と同じです。
巻線の特性は全部同じですので、次の関係式が成り立ちます。

つまり電流値は全部同じ大きさになります。
これで、誘導電動機は回るか?
ご心配無く。ちゃんと回ります。
では、この回路は、図1に当てはまるものでしょうか?それとも図2に当てはまるものでしょうか?この図(図3)は図1と図2両方に当てはまります。巻線コイル側から見ると、端子間に印加された電圧は、図1、図2、図3総て同じで200Vです。
電源回路の線間電圧がどうなっていようと関係有りません。120度ずれた電圧200Vが6つの端子(UV、WX、YZ)にそれぞれ印加されれば、
それで良い訳です。
従って、コイルに流れる電流は、図1、図2、図3で総て同じ電流になります。

になります。
コイルに流れる電流が全部同じ、コイルに印加された電圧が全部同じ、つまり、出力は全部同じでP[kW]になります。(図1、図2、図3に共通。)
次に、図1と図2の線電流を比べます。

図1の線電流は、図2の線電流の√3倍です。言い換えると、図2の線電流は、図1の1/√3倍です。図1に対して、図2は線間電圧を√3倍しましたが、線電流は1/√3倍になった訳です。
度は、図2の線間電圧を下げます。
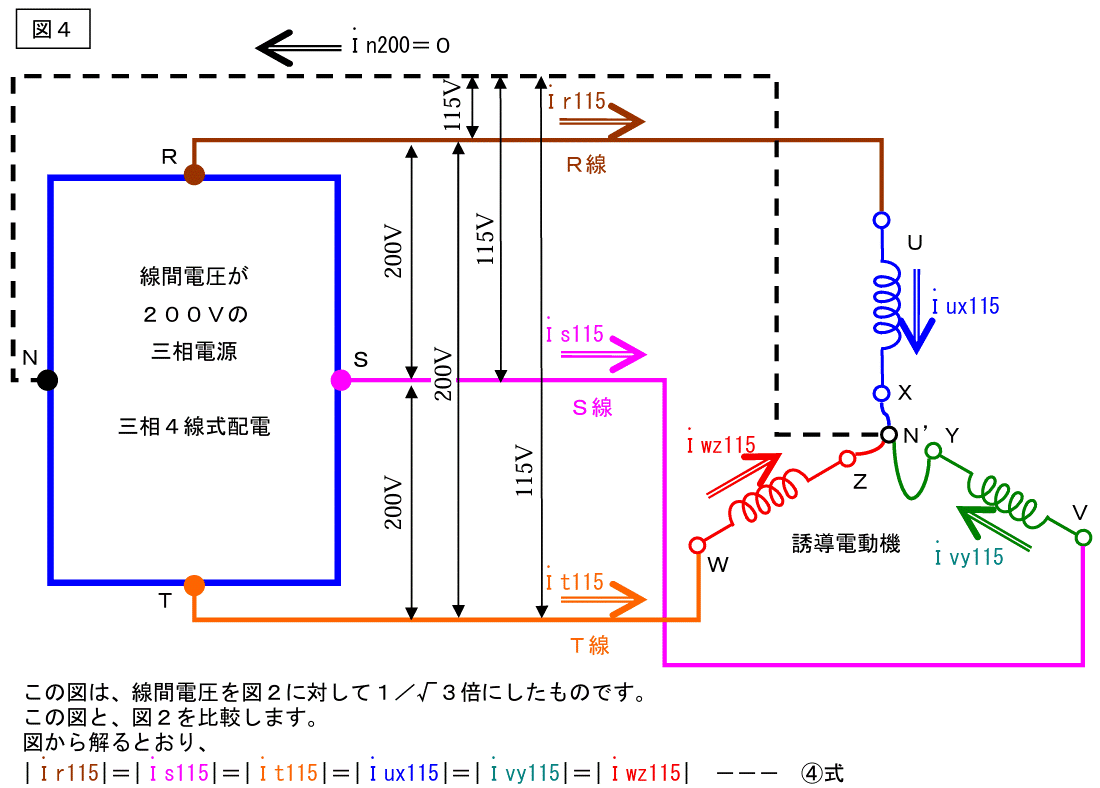
負荷のインピーダンスは変わりませんので、線間電圧を1/√3倍にすれば、線電流は自動的に1/√3倍になります。(消費電力は1/3になる。消費電力は電圧の2乗に比例。)
つまり、図4の線電流は図2の線電流×1/√3倍になります。図2の線電流は図1の線電流×1/√3倍でしたから、図4の線電流は図1の線電流×1/3倍になります。図4からN線を撤去します。
そうすると、この図は、スターデルタ始動のスター時の結線になります。次項参照。
下記に△結線時の場合を記載します。
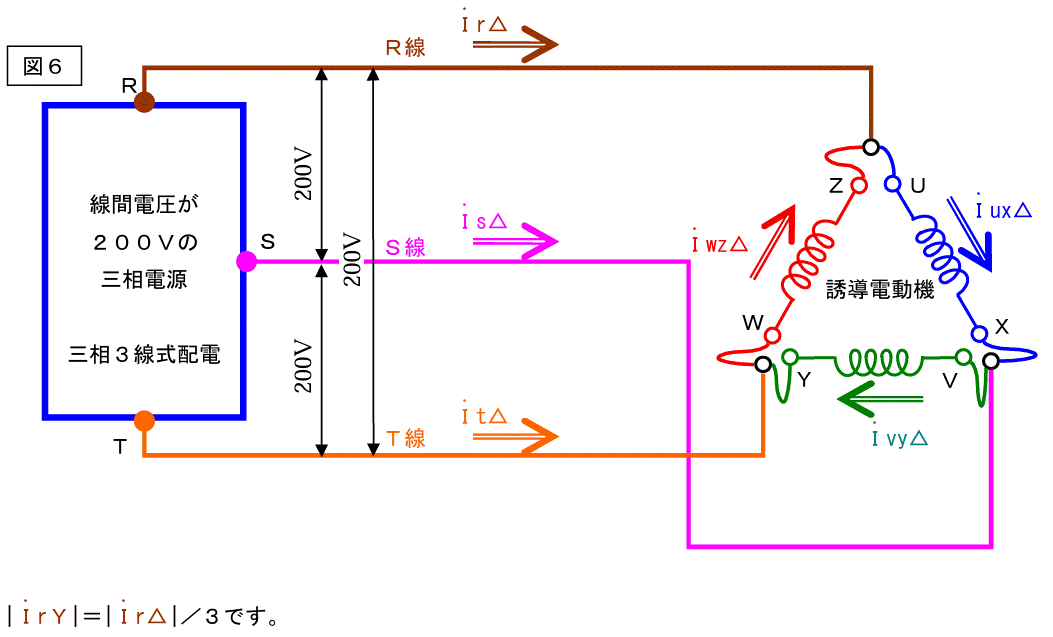
図6は普通に接続した場合の図です。電源の線間電圧は200V、誘導電動機巻線の結線はデルタです。
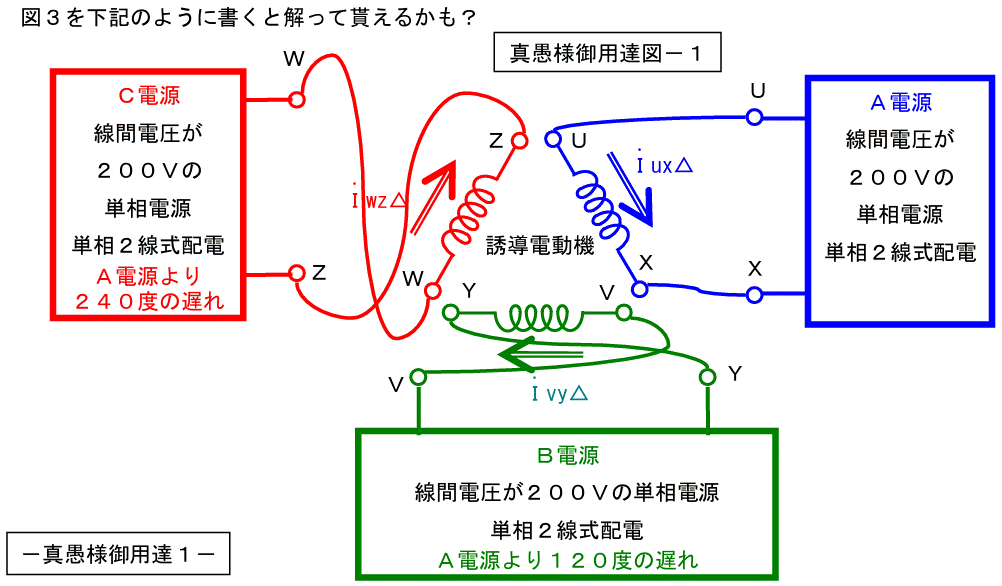
図3は怪しげな結線図です。

図3を下記のように書くと解って貰えるかも?
デルタに接続した場合の巻き線電流の算出方法です。
巻線電流は線電流の1/√3倍になります。これを証明します。
前ページの図6を使って説明します。

A点に注目してキルヒホッフの原理を導入し、流入する電流をプラス、流出する電流をマイナスとすると下記の方程式が得られます。

このままでは当然の話としてこの方程式は解けません。(変数が6個有って、関係式が3個しか無い。従って絶対に解けない。)
ここで出来るだけ計算を簡略化して、解答を導き出す事を考えます。

さらにこの式をベクトルオペレータを使って変形します。ベクトルオペレータとは120°ずつ位相のずれたベクトルを扱う時に使用する複素数です。次項に解説を記載します。
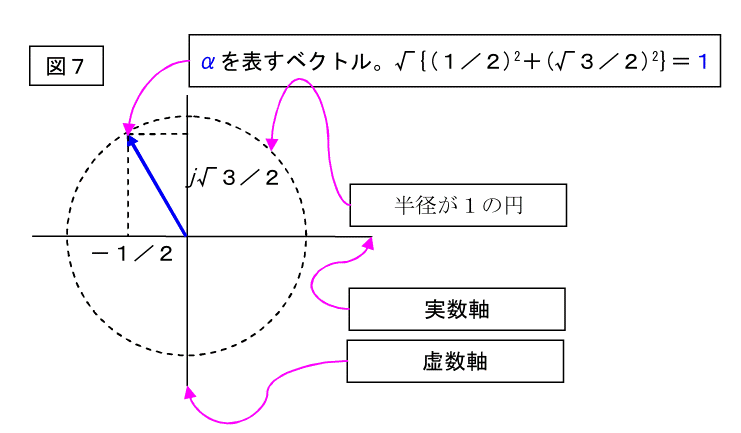
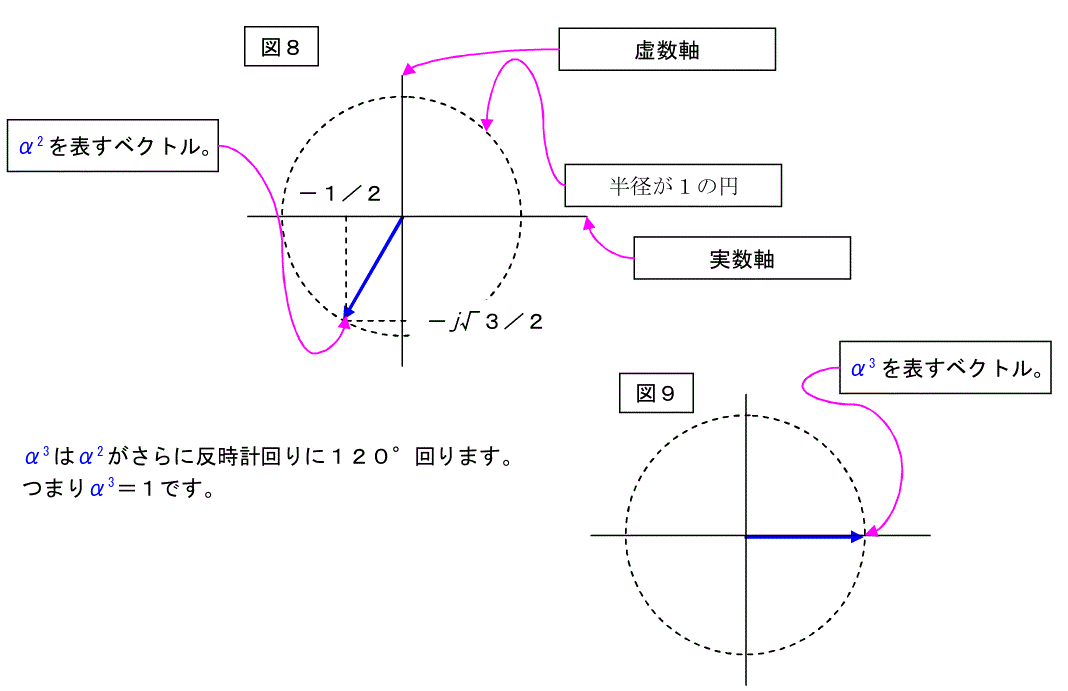
ベクトルオペレータをαと書きます。
α=-1/2+j√3/2という複素数です。
これは下図の値を持つ長さが1のベクトルです。
つまり、1∠120°(長さが1、角度が120度)と等価です。
又、∠120°は∠-240°と等しくなりますので、αは下記のように書けます。
α=-1/2+j√3/2=1∠120°=1∠-240°
α2は次のようになります。
α=-1/2+j√3/2だから
α2=(-1/2+j√3/2)の2乗
=1/4-j√3/2-3/4
=-1/2-j√3/2
=1∠240°=1∠-120°

今度は右辺の変形を試みます。巻線コイルに流れる電流の電流値は未だ解りません。

α=-1/2+j√3/2ですから、
I={1-(-1/2+j√3/2)}・Iux△
I=(3/2-j√3/2)・Iux△
Iux△=I/(3/2-j√3/2)
Iux△=I/{√3×(√3/2-j1/2)} <=結果が解っているのでこの様な不思議な変換が出来ます。
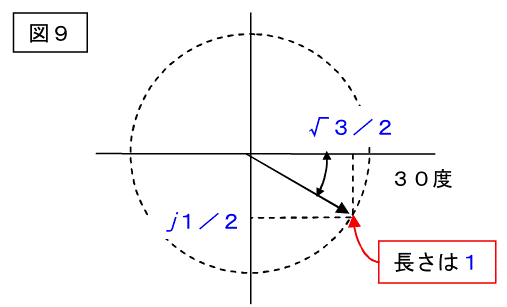
この式のアンダーラインの部分(√3/2-j1/2)に注目します。
これをベクトル座標に書いてみると下記の様になります。
長さが1で30°遅れのベクトルになっています。
従って、この式は次のように変改できます。

コメント