変圧器の温度上昇が規定内であることを確かめるために温度上昇試験を行いますが、このために変圧器に「負荷」をかける必要があります。ですが、大容量変圧器では定格負荷をかけること自体が困難ですし、大変不経済となります。そのため、返還負荷法もしくは等価負荷法という方法があります。
返還負荷法の話
皆様こんにちは 今回は電力用トランスの試験の話を書きます。
こんな話を覚えても、実社会でどの程度役に立つのか不明ですが、知らないより知っていた方が良いと思います。何かの話のネタにでもなれば幸いです。

平成 鹿年 骨月 吉日
貧電工附属 埼玉ドズニーランド大学(SDU)学長 鹿の骨
トランスは他の多くの電気機器と同様に試験があります。試験の種類は沢山ありますが、今回のお題は「温度試験」と呼ばれる試験です。
トランスも電気機器ですから、普通の使用状態で発熱します。発熱しますから、トランスが熱くなります。当然、許容限度があるわけですが、作ったトランスの発熱が限度内に納まっているかどうかを、この試験で確認します。
従って原則として、トランスに負荷をかけて一定時間(時間数は知りません。)測定します。印加する電圧も定格電圧をかけます。当然、定格電流が流れます。100[kVA]以下程度のトランスでしたら、ダミー負荷(例、水抵抗)を接続して計測すれば測定は可能です。ダミー負荷を接続して試験を行うと、当然の結果として電気代がかかります。耐久試験の意味もありますので、72時間試験などというものもあるのかも知れません。
ここで問題を出しますので考えて下さい。
[問題]
単相5万KVAのトランスが2台ある。
このトランスの温度試験を行う方法を考えなさい。
[怪盗その1]
逃げる!
5[kVA]だと思っていたので、試験当日に、スキを見つけて逃亡する。こんな試験は出来るわけナイジャン! ゴマンだと! アッタマオカシインじゃないのか?敵前逃亡・・・市中引き回しの上、鞭打ち百叩き!!
[怪盗その2]
データを捏造する。
どうやっても出来ない試験だから、ヤッタ事にして嘘八百のデータを作って誤魔化す。製品を売り飛ばした後は、事態が発覚する間に、廃業して雲隠れする。悪質につき、市中引き回しの上、逆さ貼り付け鞭打ち百叩きの後、全財産没収!!
[怪盗その3]
実負荷をかける!
5万×2なので10万になる。この様な超大容量の負荷は買電からは取れない。と言って自家発でも出来ない。仕方が無いので、電力会社の小規模発電所を貸し切りにして借りる。水抵抗の水は、海を使う。つまり臨海していないと出来ない。
電極の大きさは?枚数は?使うケーブルの種類は?不平衡はどうするの?・・・知るか!!100kW用抵抗器×1000セットダァ!・・・文句があるかぁ!!電力会社の人に多分こう言われる。「悪いことは言わない。一回病院に行きなさい。」
[解答その4]
電流だけ実際と合わせた試験をする。
二次側を短絡して、一次側から二次定格電流を流せるだけの電圧を印加する。こうすると、定格電流は流せる事になる。(印加する電圧は小さい。)定格電流を流すことが出来るので発熱は起きる。
因みに、この時印加する電圧の値はパーセントインピーダンス電圧である。この方法は「等価負荷法」と呼ばれる方法である。実際にこの試験で行われる事もある。
しかし、印加する電圧が、定格電圧では無いので、インチキと言われたら立つ瀬がない。
[解答その5]
その他の方法を考える。
その1~5までを記載しましたが、次ページ以降にその5の方法を記載します。「返還負荷法」と呼ばれる方法です。世の中、頭の良い人がいるものだと感心する方法です。
下図は返還負荷法の結線図です。
これを見ただけで、内容を理解出来る人は頭が良いと思います。
因みに小生はこれを見て全く理解出来ませんでした。ナンジャコリャ??
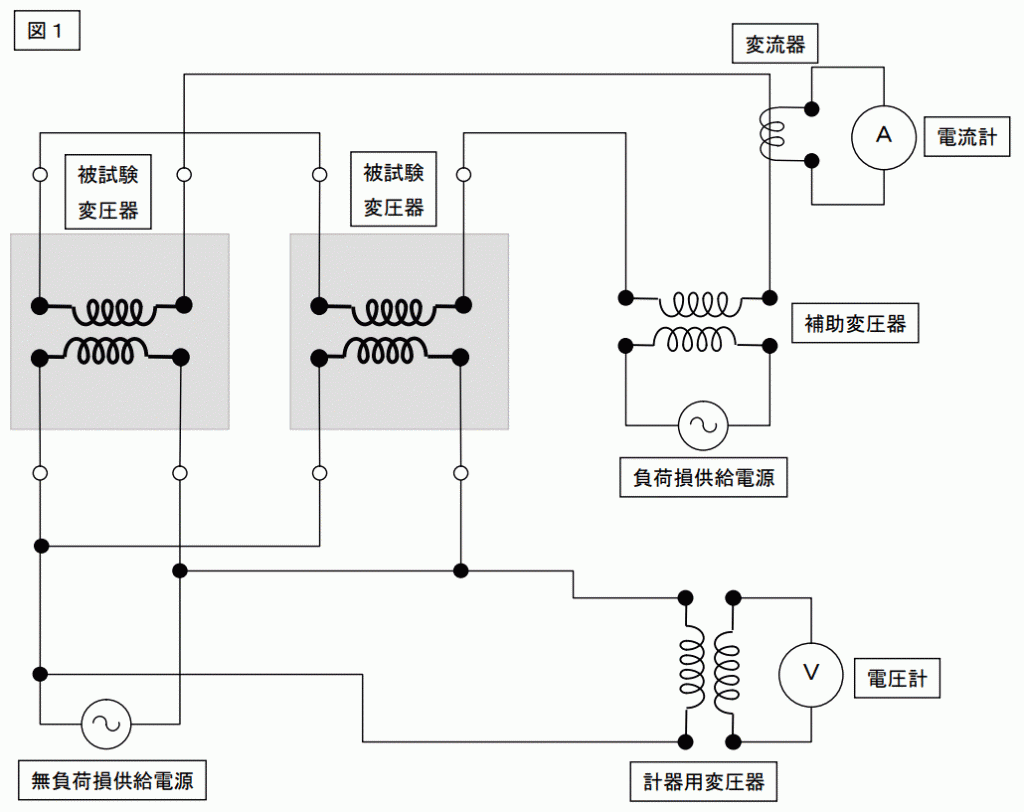
ワケガワカランです。
取り敢えず被試験変圧器は図面向かって下側が一次側、上側が二次側です。電圧計と電流計が付いていますが、これは定格値をチェックするためのものだと思います。無負荷損供給電源?意味不明です。
負荷損供給電源?これも意味不明ですし、結線の仕方が何かヘンです。
せめて相記号ぐらいはふってくれると理解するヒントになると思いますが、世の参考書はこの程度です。これで理解しろと言うほうが無茶です。こんな図で解るはずがありません。
次ページ以降に、小生の悪い頭で考えた内容を記載します。ホントにコレで、逃げなくても良く、身ぐるみ剥がされて袋だたきに遭うこともなく、病院に行くことも無く、インチキ呼ばわりされる事も無くなるのでしょうか?
まず下図をご覧下さい。
この二つの回路は「電気的に等価である。」と言えます。加える電圧が同じで、流れる電流も同じです。従って、等価であると言えます。
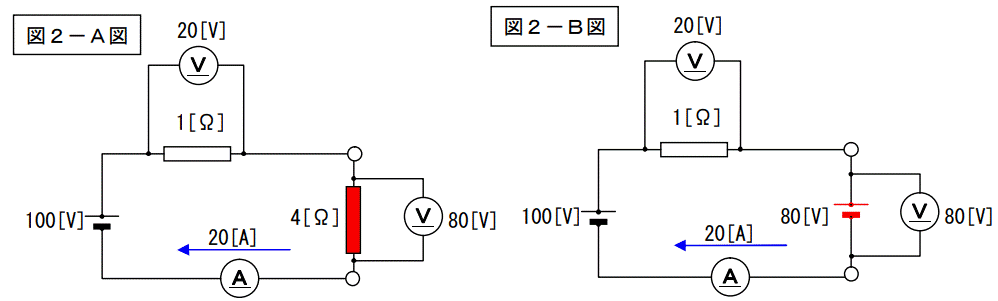
電流値が20[A]ですから、
A図では1[Ω]×20[A]×20[A]+4[Ω]×20[A]×20[A]=400[W]+1600[W]=2,000[W]
B図では1[Ω]×20[A]×20[A]=400[W]
AとBでは消費電力が随分違います。100[V]の電流容量はA図B図とも共通で20[A]が流せるものでなければイケマセン。B図の80[V]電源も電流容量は20[A]のものが必要です。今度は下記の電流値を考えて下さい。
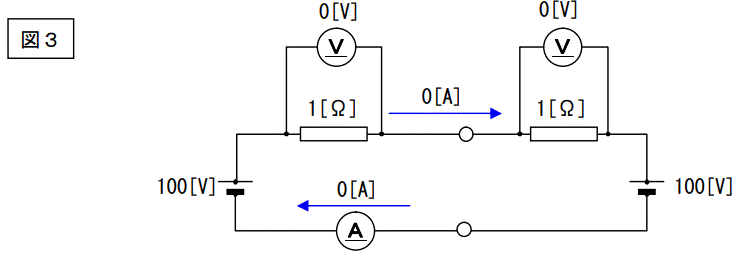
考えるまでもなく、この電流は0[A]です。つまり電流は流れません。
この図は「図2-A図の抵抗値■を撤去したもの」を2組用意してつき合わせたものです。同じものが2組と言うことを覚えておいて下さい。重要!!消費電力は当然0[W]です。では下図は?
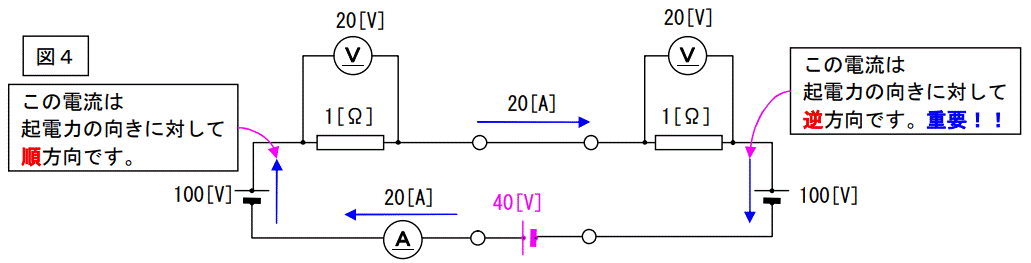
この図は図3に40[V]電圧源を挿入したものです。この図では電流値は20[A]となります。
左側の100[V]電圧源に対して電流は順方向ですが、右側の100[V]電圧源に対しては逆方向になっていることに注意して下さい。
総ての電圧源の電流容量は20[A]のものが必要なのは言うまでもありません。
消費電力は、1[Ω]×20[A]×20[A]×2=400[W]×2=800[W]となります。
こんな図を描いてみました。図4から100[V]電圧源を2つとも撤去したものです。20[A]の値が先に決まっていた場合、挿入すべき電圧源の電圧を求める図です。直感的に計算出来ると思いますが、?=40であることは直ぐ解ると思います。
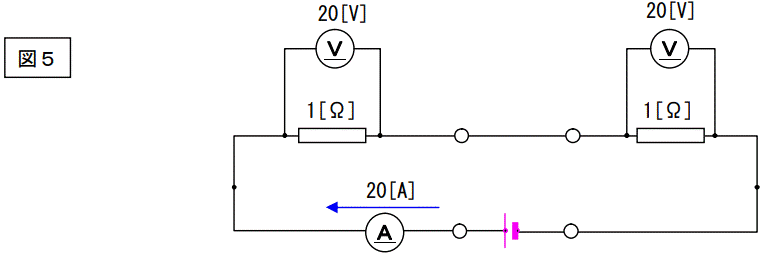
図4と図5を見比べて下記のことを理解して下さい。「図4の100[V]電源×2セットは回路電流に無関係。」つまり電流を計算するときに、あっても無くても同じです。
さて、下図はトランスの等価回路ですが、励磁回路部分を撤去した回路です。
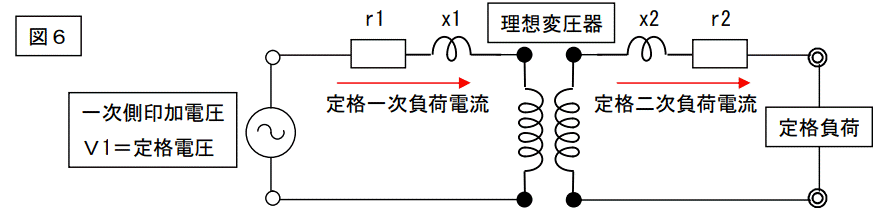
この回路を二次側に換算した回路が下記です。
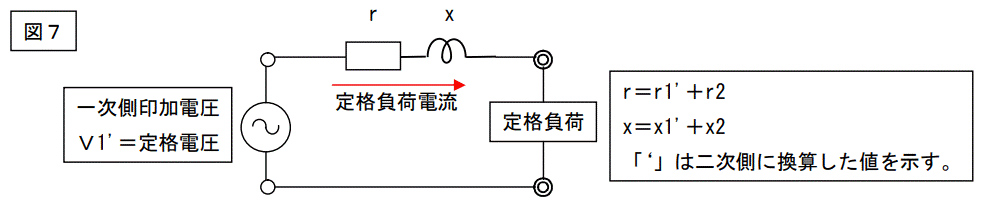
上図の回路で示されるトランスを2セット用意して、下記のようにつき合わせます。
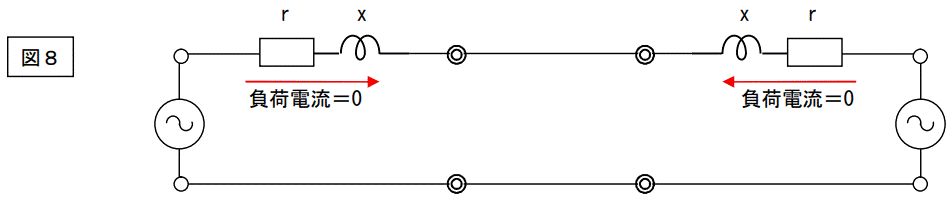
見覚えのある回路になったと思います。この回路は、図3の回路を変形したものと考えて下さい。電源を直流から「交流」に置換し、抵抗を「抵抗+リアクタンス」に置換したものです。電流はこの回路では流れません。この回路に図4と同様の電圧電源を挿入します。
電圧電源を挿入してみました。
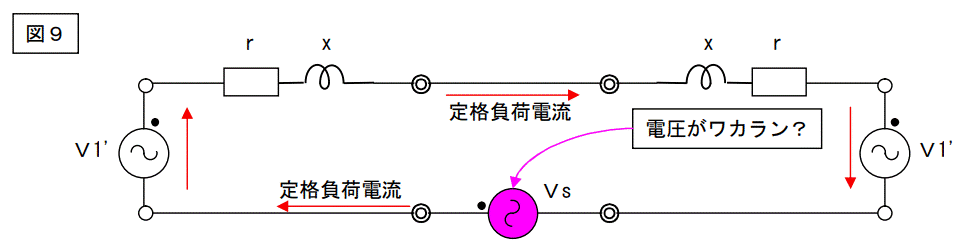
この図の「●」は極性を示します。
元々あった左側の交流電源には定格負荷電流が順方向に流れ、右側は逆方向です。挿入する電圧電源の電圧が解りません。この電圧を決めるものは、このトランスの%インピーダンスです。
トランスに定格電流を流した時に起きる電圧降下はIZですが、%Z=IZ÷V×100です。従って、挿入すべき電圧の値は(%Z×定格電圧÷100)×2倍になります。今、仮に%Zが3%だったとします。挿入する電圧の値は、Vs=定格電圧×3%÷100×2倍です。
冒頭のワケのワカラン問題で考えてみましょう。
電圧値を書いて無かったのですが、P66kV/S3.3kVとします。パーセントインピーダンスボルト=3%
従って挿入する電圧Vs=3300×3%×2=198[V] となります。次に、この電源を挿入するための電源容量を計算します。電源容量=電圧×電流ですから、まず電流値を計算します。
定格電流In=定格容量÷定格電圧
=50000[kVA]÷3.3[V]
=15,152[A]
電源容量=電圧×電流
=198[V]×15,152[A]
=3,000[kVA]
となります。
つまり、挿入する電圧電源の容量は、被試験トランスの容量×%Z×2倍となります。%Zが4%だったら4,000kVAになり、2%だっらたら2,000kVAです。相手が50,000[kVA]と言う途方も無い容量ですから、この程度の試験電源容量は必要です。
挿入する電圧電源の電圧値が、%Zの値に依って色々な値になります。3%の場合は旨い具合に200[V]程度になりますから、200[V]トランスを持ってくれば何とかなりそうです。264[V]や 132[V]の場合は、実際どうやるのかは解りません。何方がご存じでしたら教えて下さい。次のページに、この試験で電流がどの様に流れるか描いてみました。
一次側の電圧は66kVですが、この図は二次側に換算した電圧3.3kVで記載しています。
下図に示した様に、一次側の電源は、電圧を印加する為だけに存在し、電流は下図のような流れになります。従って、一次側の電源容量はゼロです。
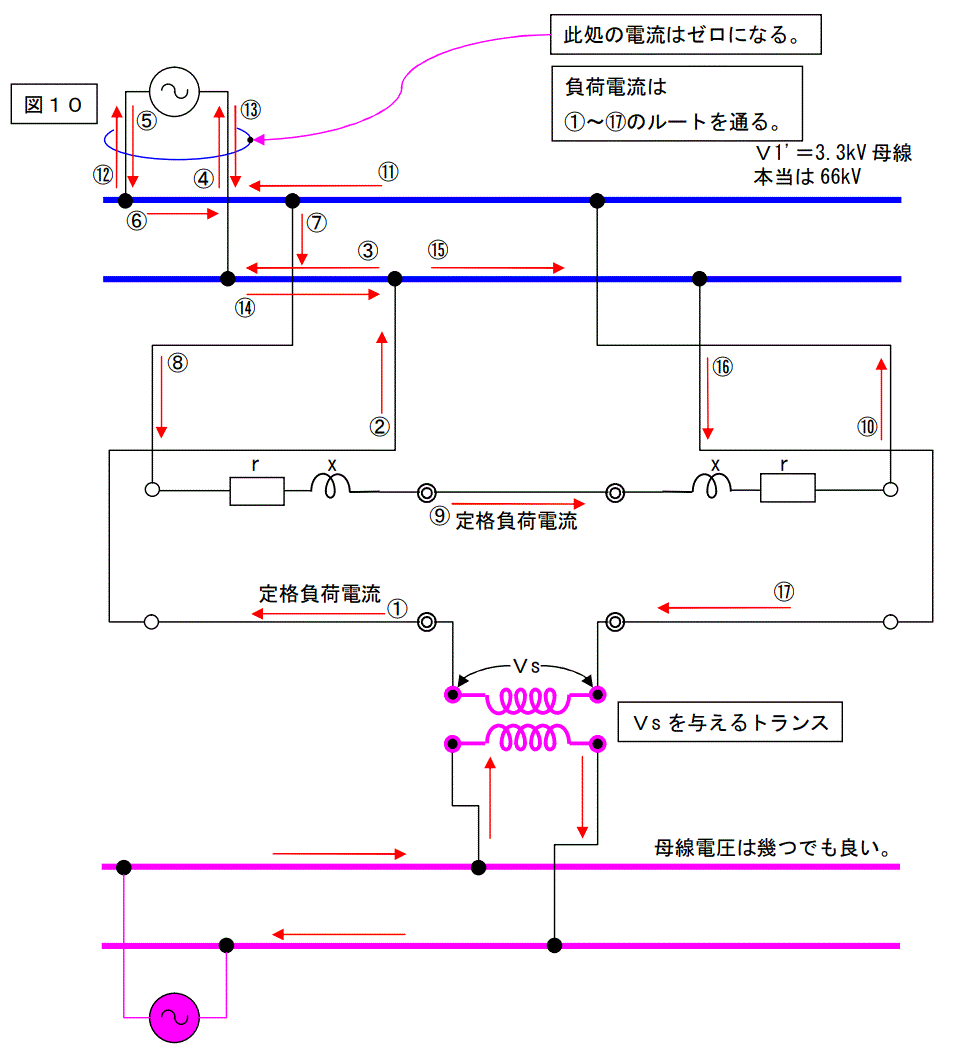
ピンクで描いた電源は図のように、挿入する電圧と、負荷電流を供給しています。つまり、この電圧電源でトランス負荷回路皮相電力を供給しています。実際に消費される電力は有効電力ですから、このトランスは負荷損を供給するトランスと言うことになります。
もの凄く重要!!
この様にピンクで描いた部分が2ページ図1の負荷損供給電源及び補助変圧器です。
仮に、%Z=3%で=1.8%+J2.4%(5:3:4の比率)だとしたらこの負荷損供給電源の電源容量は下記になります。
皮相電力=3000[kVA]
有効電力=皮相電力×力率=3000[kVA]×0.6=1800[kW]
もの凄い発熱をします。
さて次ページは、図1の無負荷損供給電源に関して記載します。
前ページまでは励磁回路を無視していましたが、今度は考慮してキチンと図に描いて見ます。下図に示す励磁コンダクタンス及び励磁サセプタンスは二次側に変換したものです。
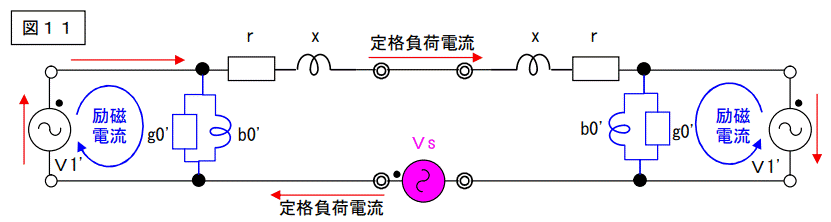
この回路図見ると、励磁回路のコンダクタンスとサセプタンス部分にも負荷損供給電願から電流が回り込むように見えますが、負荷電流と励磁電流は独立して流れます。
下記に、「重ねの理」を用いて説明図を付けます。
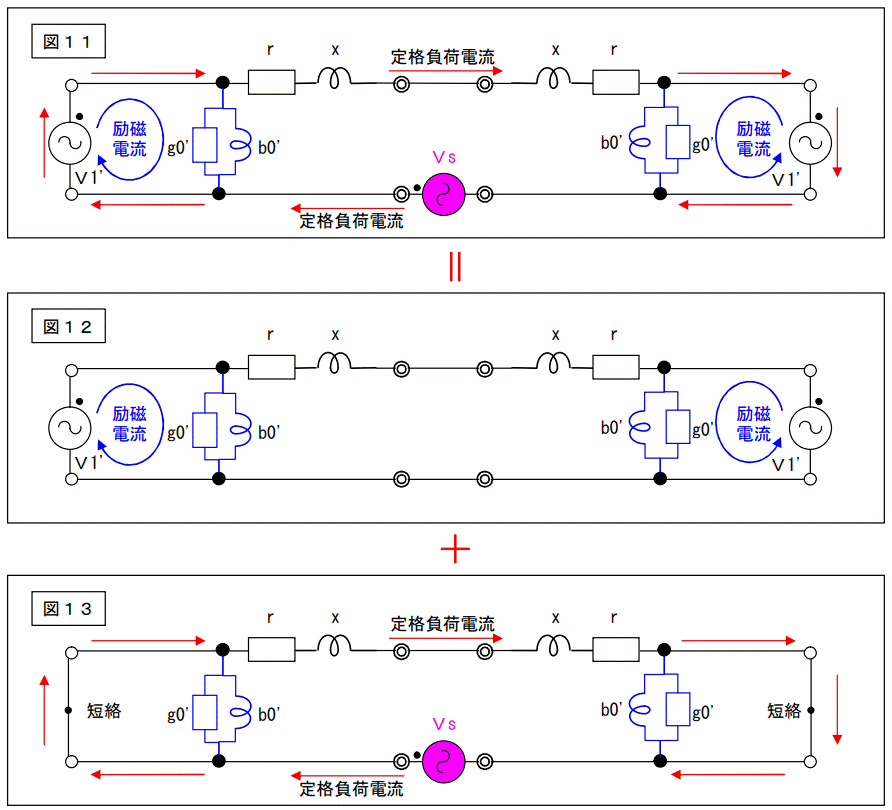
この様に、2つの回路は各々独立していますので、励磁回路には励磁電流しか流れません。鳳・テブナンの定理を用いても証明出来ると思いますが・・・ヨクワカラン!この回路図(図11)を用いて電源容量を検討して見ましょう。
図10に励磁経路を追記して見ます。青い線が励磁電流の流れです。(負荷電流は図が煩雑になるので記載しませんでした。)
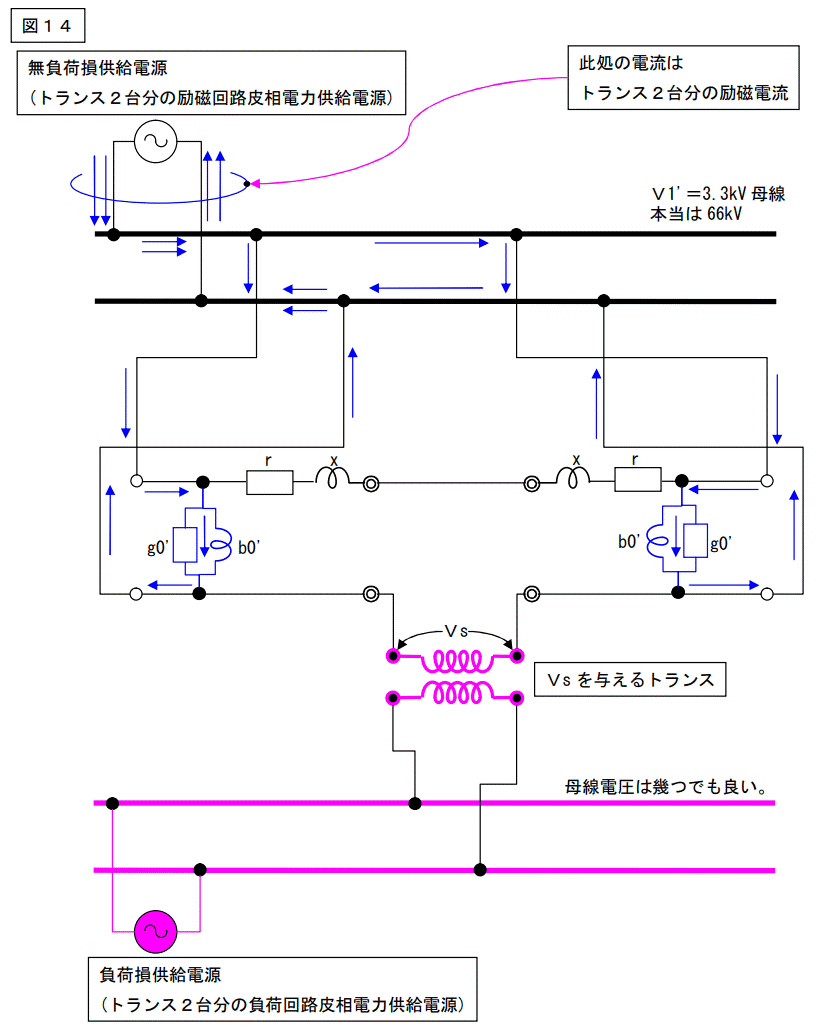
この様に、トランスの一次側に接続した電源は、励磁回路のみを賄う電源となります。従って、無負荷損供給電源になるわけです。
仮に、励磁電流を全負荷電流の2.5%とします。この場合、無負荷供給電源の容量は、トランスの定格容量×2.5%の2台分。
50000[kVA]×2.5%×2=2500[kVA]となります。
無負荷損を定格容量の0.1%とすると、このトランス1台当たりの鉄損は
50,000[kVA]×0.1[%]=50[kW]
となります。
トランスが2台ですから、全無負荷損計は50[kW]×2=100[kW]となります。
前項で計算した負荷損計が1800[kW]、今回計上した無負荷損が100[kW]ですから、合計で1900[kW]になります。電源容量は3000[kVA]+2500[kVA]=5500[kVA]が必要です。
元々が50,000[kVA]×2というとてつもない容量ですから、必要電源容量が約1/20の5500[kVA]で済むことは画期的な事だと思います。
従って、お金は多少かかりますが、冒頭で書いたような酷い事にはならないようです。勿論、今まで設定してきた%Zや無負荷電流の値は総て適当です。この様な超大容量変圧器の諸値が幾つなのかは良く解りません。一般的に%Zは小さい方が、電圧変動率や効率の面から見て良いのですが、遮断容量が追いつかない場合などは敢えて%Zを大きくすることがあります。
実際の値がどの様なものになっているか、ご存じの方がいらっしゃいましたらお教え下さい。
此処までで、取り敢えず説明は終わりです。ご理解頂けましたか?
何?ワカラン?そりゃそうです。これは、書いている本人が首を傾げながら書いたものです。ですから、他に説明の仕方があるのかも知れません。理解を深める為に「宿題」を作りました。お時間が有れば、挑戦して下さい。
【宿題】
前例にならい、次の場合の試験方法を考えなさい。
その1
単相トランスが3台の場合
その2
三相トランスが2台の場合
何れの場合も、容量及び電圧は適当でよい。
試験用トランスの容量及び変圧比は任意に設定可能とする。
解答は、試験用の結線図のみの提示でよい。
【宿題 その1の解答】
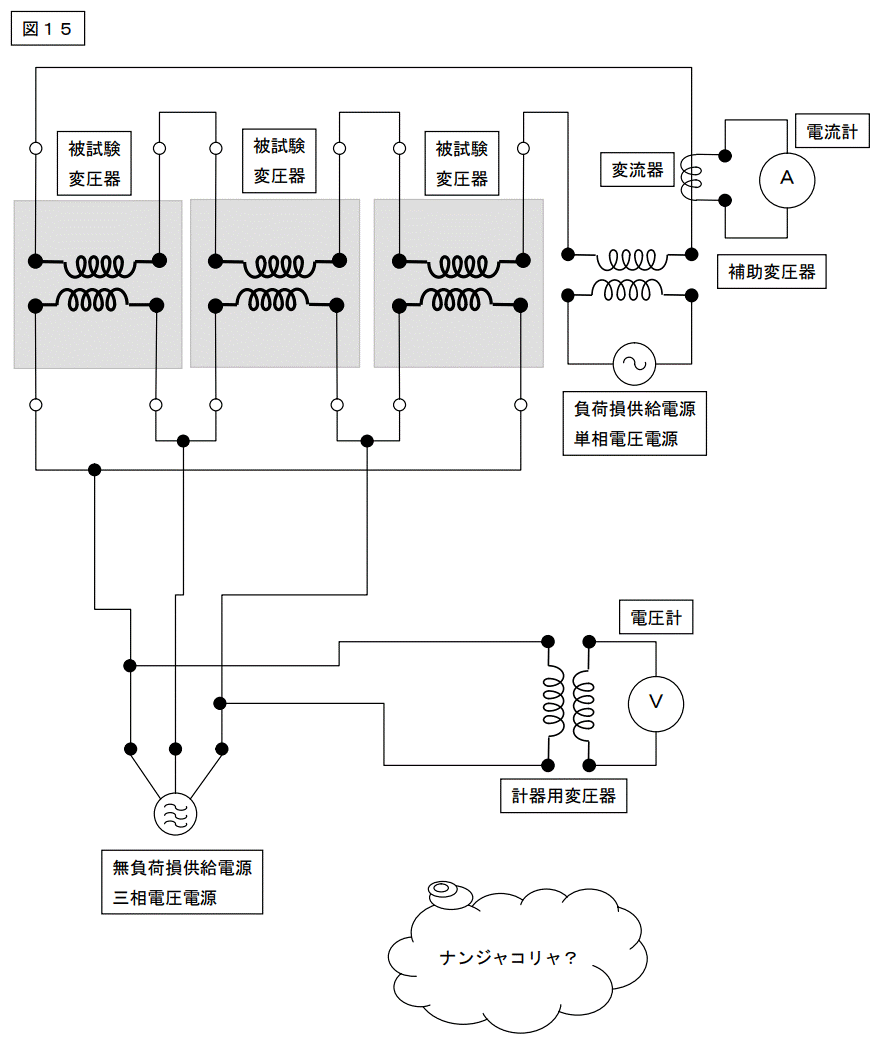
【宿題 その2の解答】
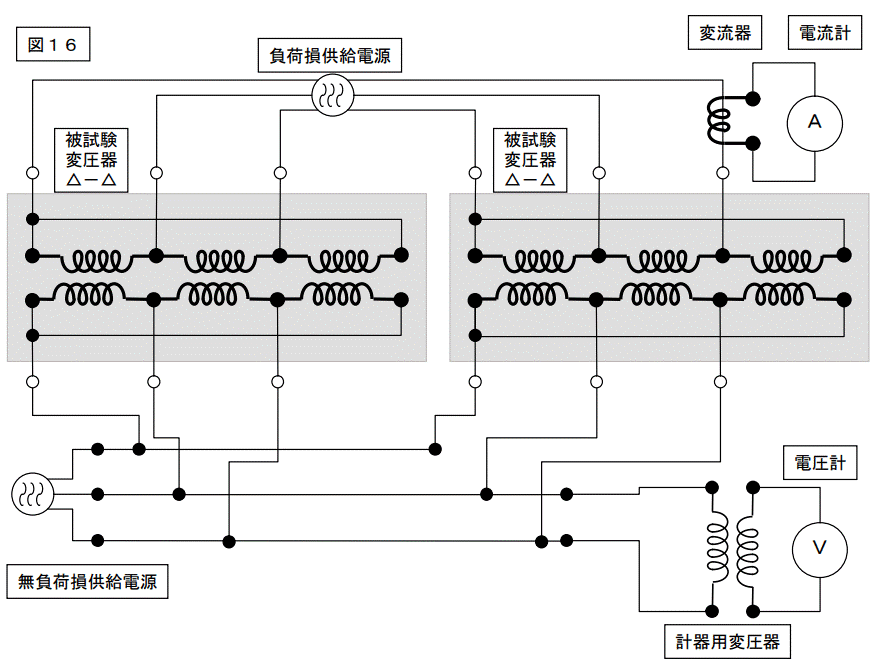
イヤー・・・ワケワカランです。
専門書に書いてあったものを多少変形して書いています。間違いは無いと思います。
これで多分試験ができるのでしょう。負荷損供給電源の結線部分の書き方が変です。
多分、RSTをひっくり返していると思います。三相の場合でY-△の場合や、Y-Yの場合はどうなるのでしょうか?モォ~ワカンナイ!
しかし、世の中頭の良い人はいるものです。
本日の講義はこれにて終了。
オシマイ
コメント