誘導電動機はどうして回るのかと言う話
皆様こんにちは。
普段からお世話になっている誘導電動機ですが、この電動機がどうして回るのかと言うことを考えてみようと思います。
参考書などには、「誘導電動機はアラゴの円盤が回る原理を利用して回っています。」と書かれています。これで、誘導電動機が回る原理を理解出来る人は少ないと思います。小生もその1人で、全く理解出来ませんでした。
仕方が無いので、独自に回転原理を考える事にしました。この記載が、何かの役に立つことを期待します。

平成 鹿年 骨月 吉日
貧電工附属 サイタマ・ドズニーランド大学 学長 鹿の骨
取り敢えず下記の図を見て下さい。
アラゴの円盤及び実際の誘導電動機の写真です。
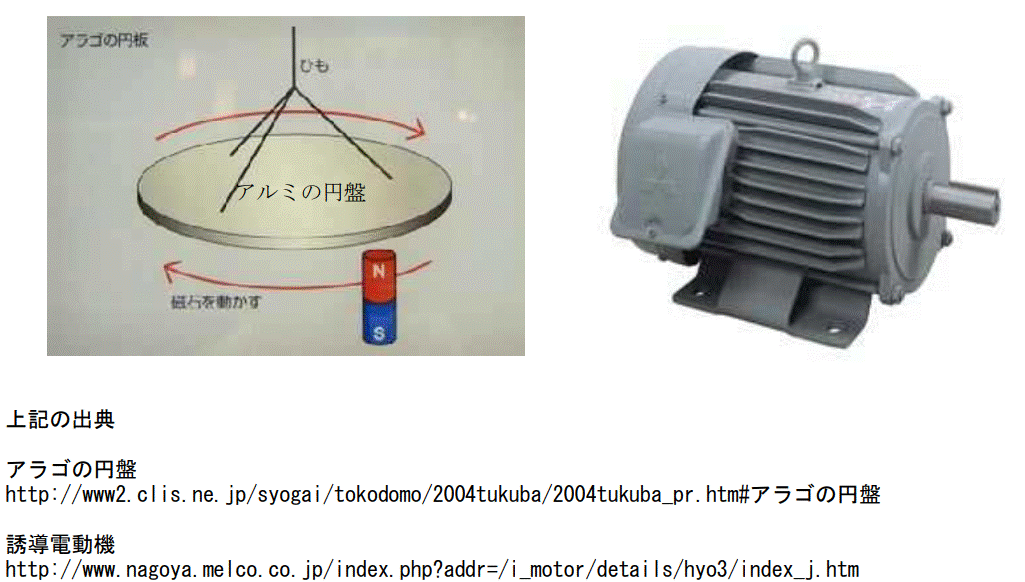
アラゴの円盤は磁石を円周方向に動かすと、アルミの円盤(非磁性体)が回るというものです。
鉄製の円盤でしたら、磁石に引っ張られて回ることは容易に理解出来ますが、磁石には反応しないアルミの円盤が回るのがミソです。
しかし、右の誘導電動機とは似ても似つかないものです。
これで、理解しろって言われてもねぇ~・・・・。
世の中のアタマの良い人たちはこれで納得するのかも知れませんが、俺はバカだから、納得出来ません。と言って何時までも 解らない ワカラナイ とホッタラカシにしている訳にもいきません。
完全に無手勝流の解説を次項以降に書ます。尚、この記事を読むに当たり、回転磁界が何故出来るかは理解されているものとして話を進めます。又、説明途中でややこしい計算式がたくさん出てきます。
この記事はどうして回るのかが主眼ですから、細かい計算式には余り気にしないで下さい。
早速ですが下図を見て下さい。
何やら怪しげな図です。
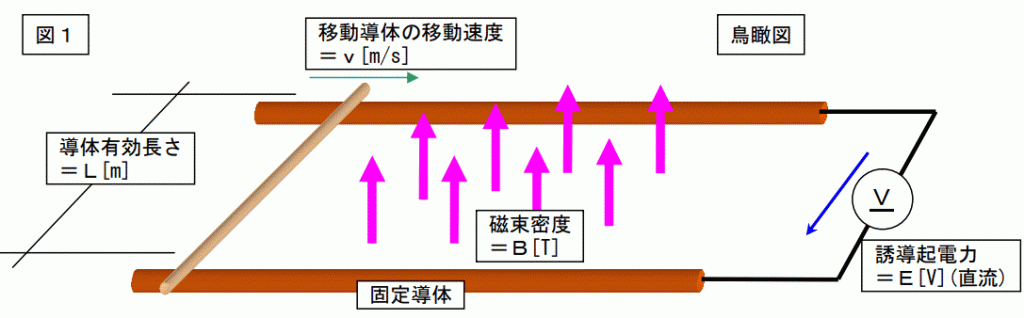
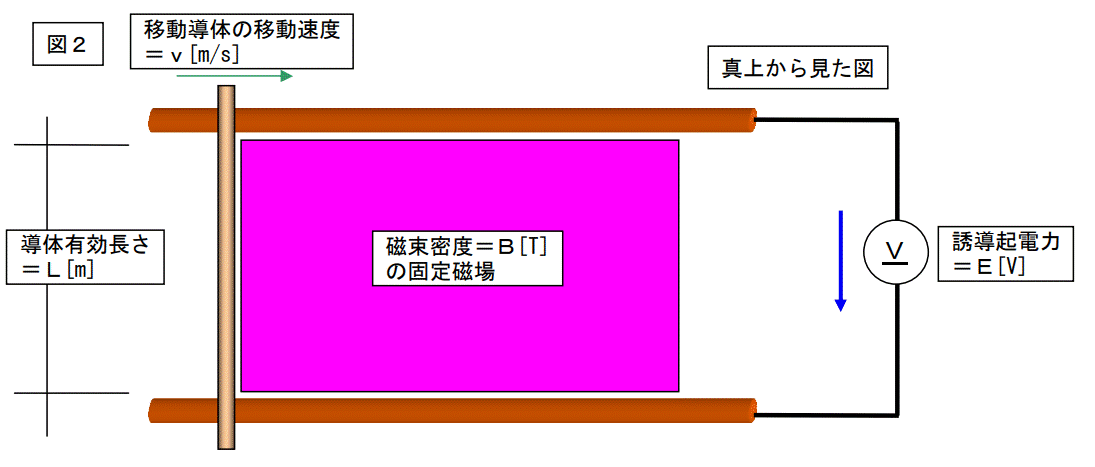

この図は「フレミングの右手則」を図にしたものです。
磁場の磁束密度はB[T:テスラ]で一定です。(1[T]=1[Wb/m2])つまり、固定磁場です。
1[Wb]って何だ?・・・・・知るか!
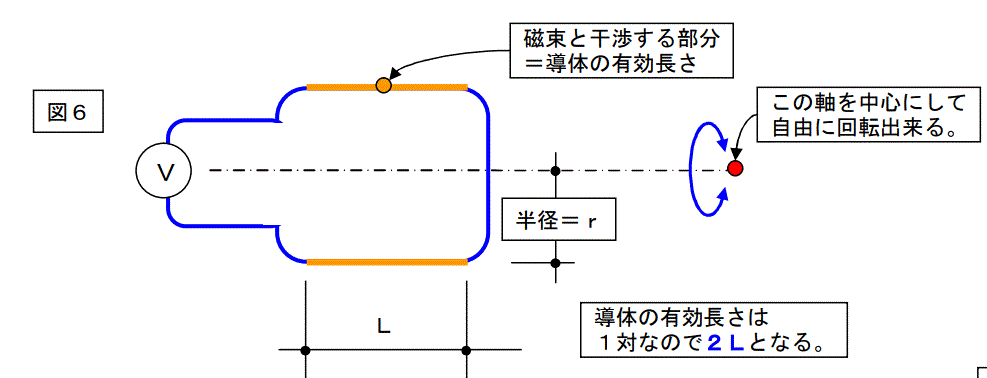
移動導体の有効長さL[m]とは、磁束を横切る部分の長さを言います。移動導体の全長の内、磁束を横切る部分は限られています。移動導体の移動速度はv[m/s]で一定です。
電圧計は内部インピーダンスが「∞無限大」で、電流は流れないものとします。
この時、各値には下記の関係式があります。
E[V]=v[m/s]×B[T]×L[m]
E=vBLです。
これをvBL則(ブイ・ビー・エル・ソクと読む)と言います。
今度は磁場を変えます。
一定磁束密度では無く、一定でない磁場を持ってきたらどうなるかを考えます。
下図の通りです。
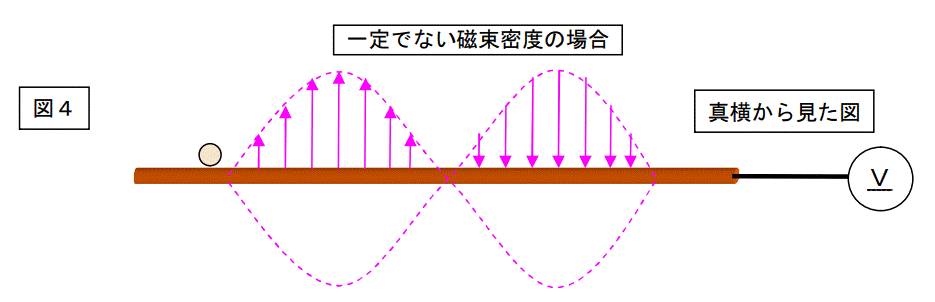
上図の様に、一定でない磁場の中を、前ページと同じように移動導体が移動した場合、誘導機電力は当然変化し直流起電力では無くなります。
ここでは、発生する電圧が変化することだけをご理解下さい。
次に下図の様な場合を考えます。
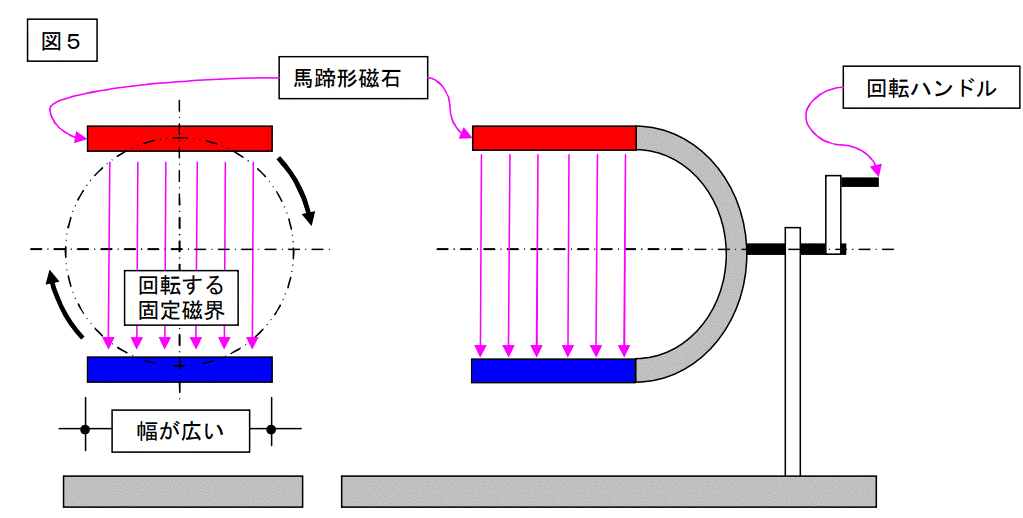
図5に示す様な、回転する固定磁場の中に、下図に示すような導体を入れた場合、どの様な電圧が発生するかを考えます。
とにかく、導体を入れてみましょう。

回転ハンドルを回します。
闇雲に回しても訳が解らなくなりますので、1秒間にf回のピッチで回すことにします。
つまり、f[rps]です。1分間に換算すると 60f[rpm]になります。
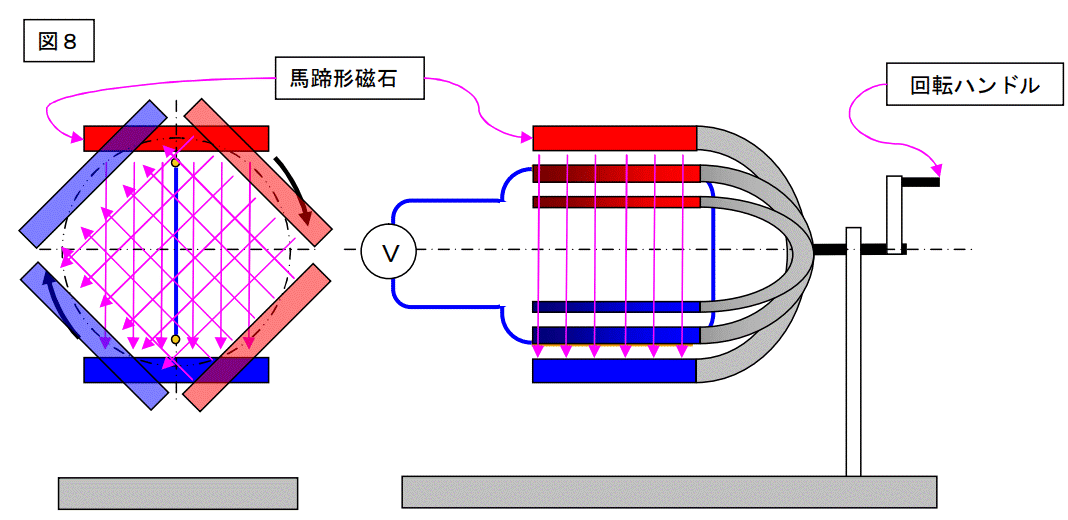
グルグル回すと、上図の様になります。
ウゥ~ン・・・訳がワカラン???
取り敢えず書いてみただけ・・・
さてと・・・。
とにかく、この動いている状態を解析しなければイケマセン。
そこで、悪いが、磁石に跨って、一緒に回ってくれ!
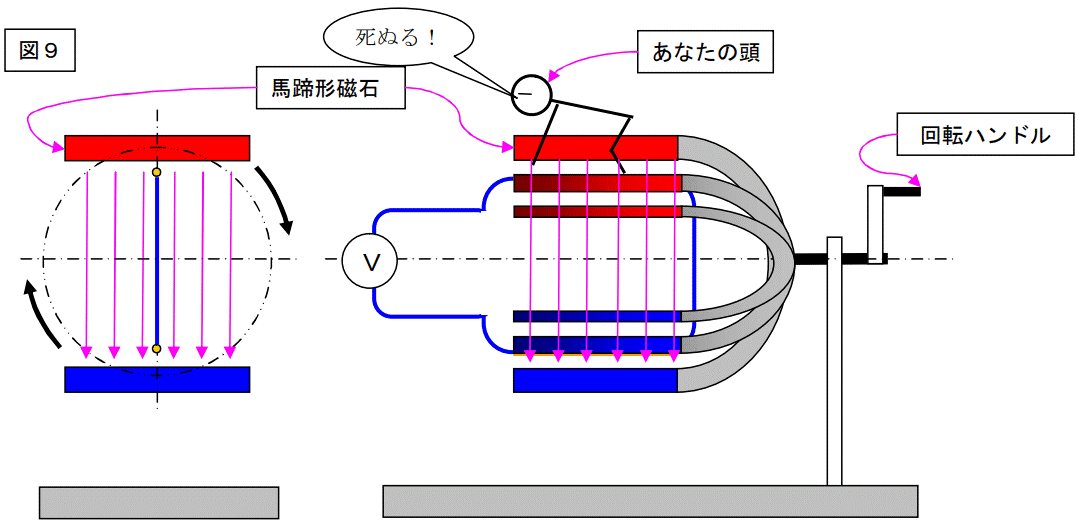
大丈夫。死ぬことは無い・・・多分?
この状態で、回転している磁石を見ると、止まって見えます。
逆に、止まっている回転子を見ると、回っているように見えます。
従って、この回っているように見える回転子が、回っていることにして、解析を進めます。
解析をスタートする時に、下記の位置関係からスタートします。

まず回転子の回転速度を計算します。(磁束を横切る速度を計算したい。)
回転子の回転半径はr[m]でした。
これが1秒間に f 回転しますから、円周の回転速度は下記になります。
回転速度=円周長さ×回転数
=直径×π×回転数
=半径×2×π×回転数
=2πrf[m/s]
この速さで回転子の導体が、2本セットで回っています。では、この導体が磁束を横切るスピードは幾つになるのでしょうか?これは、回転子と固定子の位置関係に依って、変わります。因みに、図10の位置関係にあるときは、全く横切っていません。
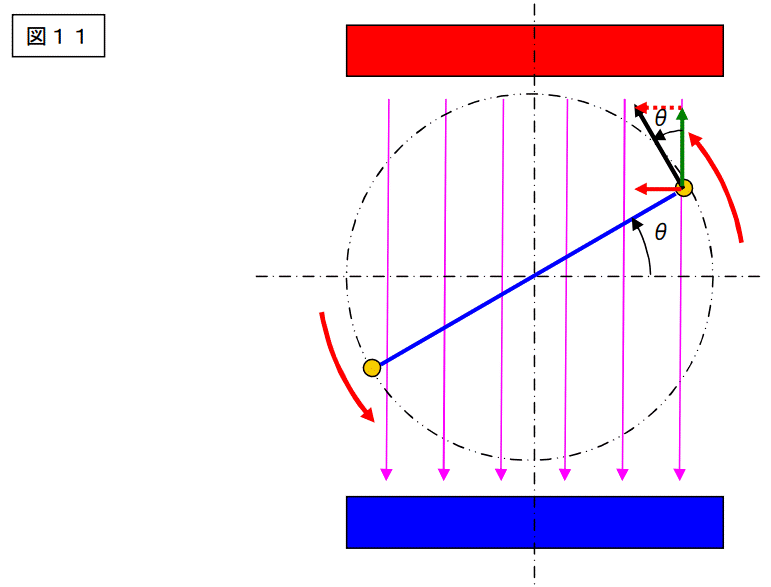
図を少し大きくして詳しく見ます。
上図のように、角度θ[rad]回った時点での解析を行います。図中の黒い矢印は、この導体の円周方向の速度を示します。赤い矢印は、磁束を横切る方向の速度に分解したものを示します。
緑の矢印は、赤い矢印と 90°方向が異なる矢印です。
この図から解る通り、赤い矢印(磁束を横切る速度)の値は下記になります。
赤い矢印=黒い矢印×sinθ
=2πrf[m/s]・sinθ --- ①
θと時刻 t の関連は下記です。(角速度で計算する。)この回転体は1秒間に f 回転しますから、角速度を計算すると、2πf[rad/s]になります。(1回転で 2π[rad]だからこうなる。)
従って、t 秒後の角度は、角速度×時間で計算出来ますからθは下記のように時間の関数として表すことが出来ます。
θ[rad]=2πf[rad/s]×t[s]
=2πft[rad]
2πf は固定された値を取りますので「ω」と置き換えます。
上記の①式は下記の②式に書き換える事が出来ます。
赤い矢印=ωrsin(ωt)[m/s] --- ②
これで、導体の磁束を横切る速度が計算出来た事になります。
発生する電圧の計算に移行します。
電圧=速度×磁束密度×導体長さ
でした。
従って
電圧[V]=ωrsin(ωt)[m/s]×B[T]×L[m]×2倍(導体が1対なので2倍する。)
となります。
この様に、回転子には交流電圧が発生します。
何と発電機になっています。 <==重要!!!
次に、この電圧がどの方向を向いているのかを考えます。
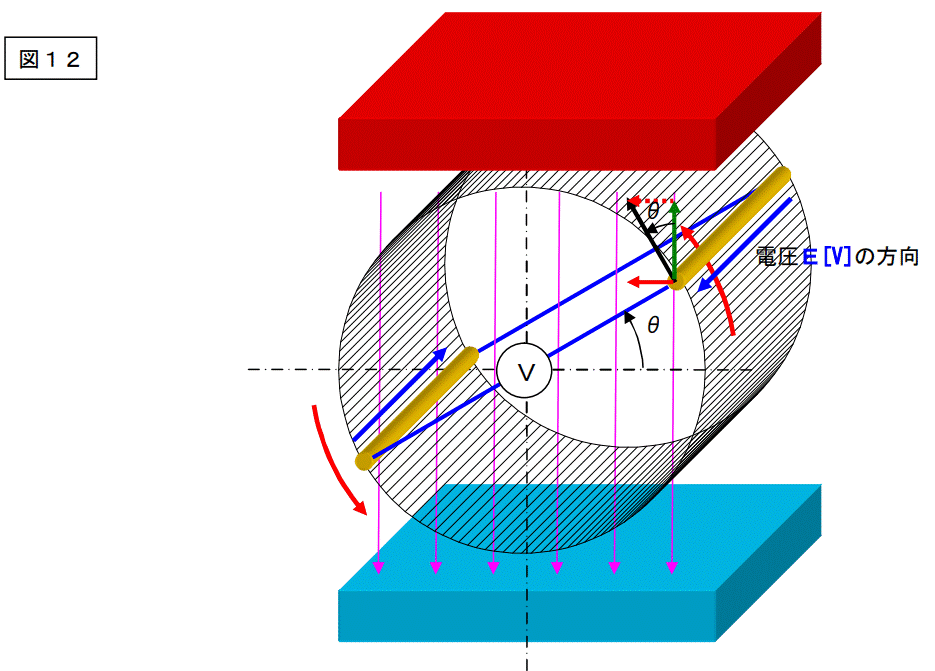
この電圧がどの方向を向いているのかは上の図のようになります。

導体の位置毎の電圧は上図の様になります。
位置によって、発生電圧が決まっています。
さて、これで電圧が発生することは解りました。
今度は、電圧計を外して、電流を流して見ましょう。
電圧が発生するのなら、電流を流すことが出来るハズです。
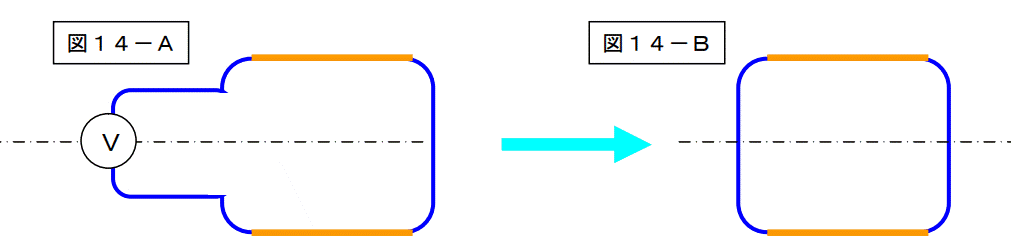
図14-Aの電圧計(内部インピーダンス無限大)があった所を短絡して、図14-Bの様にします。
これはマズイぞ・・・・。
導体にインピーダンスが無いから、流れる電流が無限大になってしまう・・・・。
と言うことで、抵抗Rを挿入します。(導体の抵抗値と考える。)
これらの解析を行う前に、「フレミングの左手則」の話を書きます。
早速ですが下図を見て下さい。又、何やら怪しげな図です。
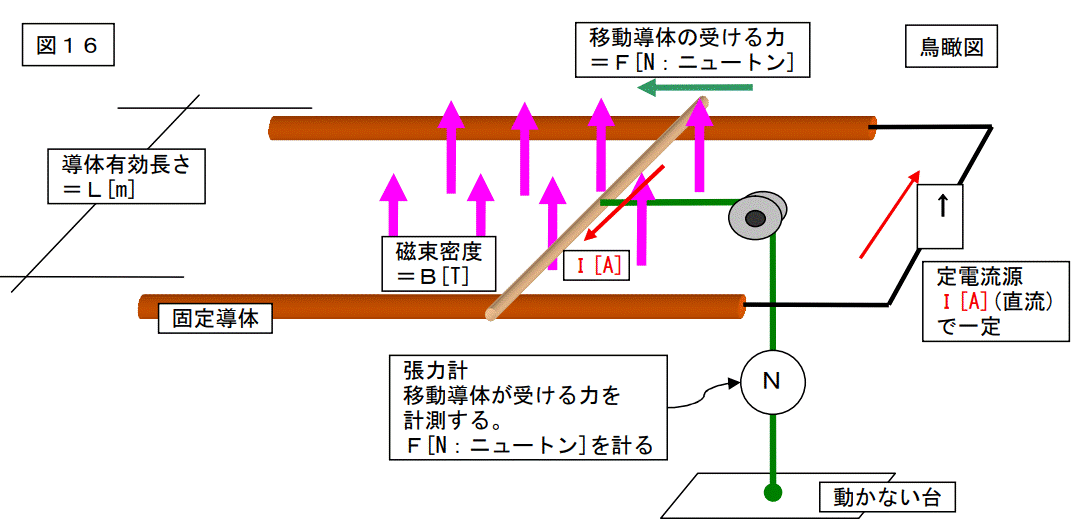
この図は「フレミングの左手則」を図にしたものです。
図に示すように、移動導体に張力計を取付け、この張力を計測すると次の計算式になります。
移動導体が受ける力[N]=F[N]
F[N]=I[A]×B[T]×L]m]
=IBL[N]
これをIBL則(アイ・ビー・エル・ソクと読む)と言います。
ここでは、磁束の中の導体に電流を流すと力を受けることだけをご理解下さい。
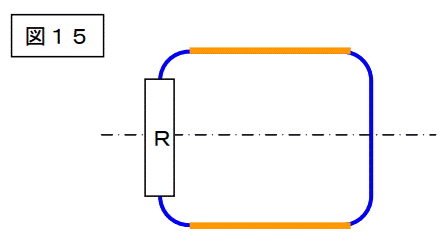
さて、図15に示した移動導体を磁束の中に入れてみましょう。
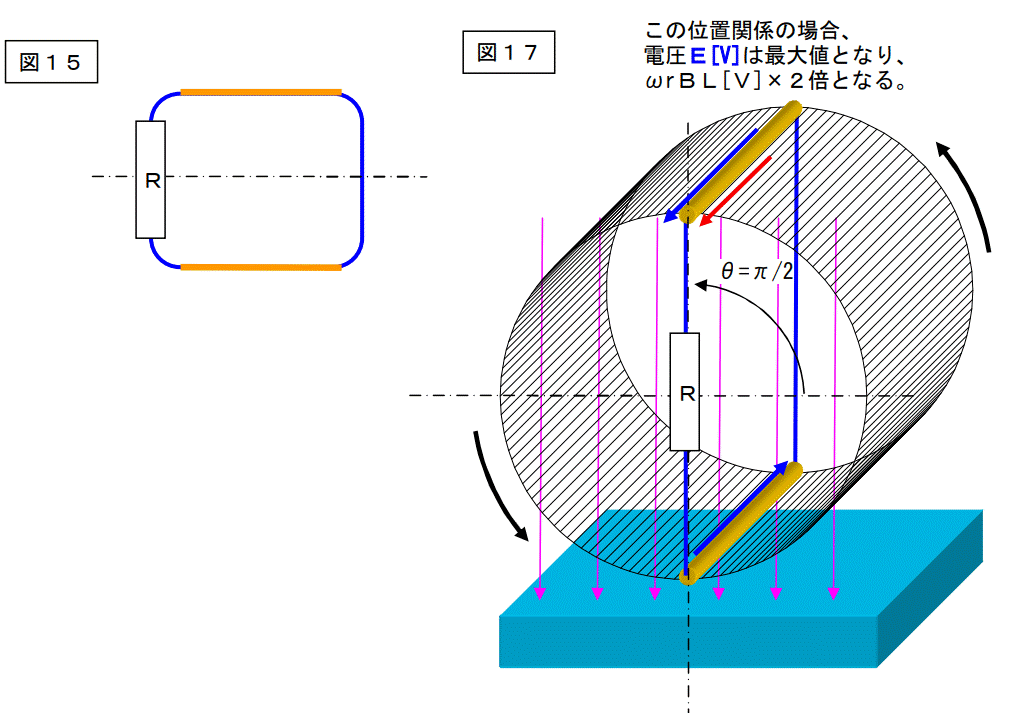
図17は移動導体内に発生する電圧が最大になる位置の場合を描いたものです。
この時に発生する電圧はωrBL[V]×2倍です。
従って流れる電流は次の計算式で計算出来ます。
電流I[A]=電圧[V]÷抵抗[Ω]
=ωrBL[V]×2÷R[Ω]
電流が流れますので、この移動導体は力を受けます。
力の大きさはフレミングの左手則をそのまま適用します。
F[N]=IBL[N]
=(ωrBL[V]×2÷R[Ω])×BL
=2ωrB2L2/R[N] <==何やら、ややこしい式になります。
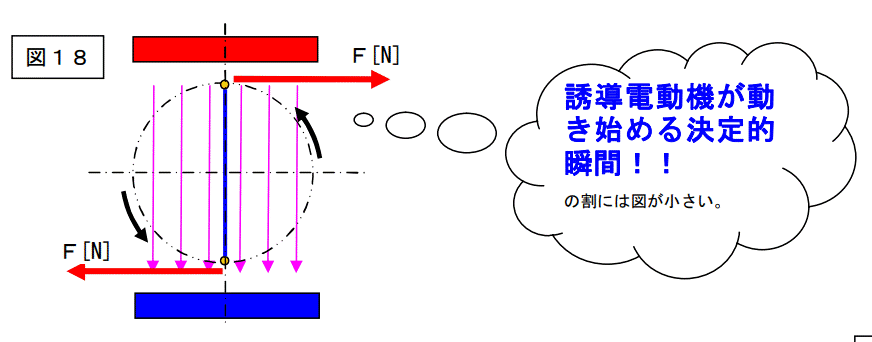
ここで、この力の方向を考えます。下図の方向になります。
つまり、回転している方向とは逆の力が働きます。
これはこの導体が回り始める事を意味します。 <==最重要項目!!!
もう少し詳しく見ましょう。

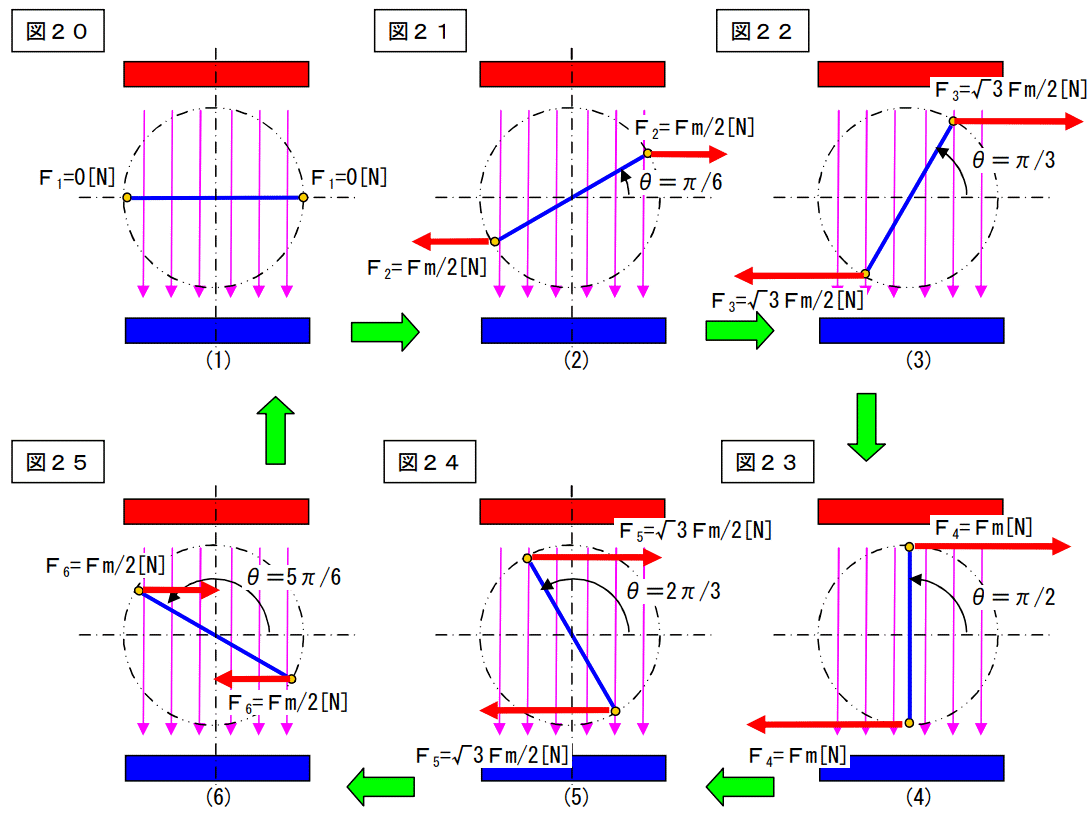
(1)のポジションと、(4)のポジションは即座に理解出来ると思います。
しかし、(2)(3)(5)(6)のポジションでは力の加わる方向と、回転方向がずれています。
この力の方向で何故、回転する力となりうるのかを次ページに示します。
図21の場合で考えます。
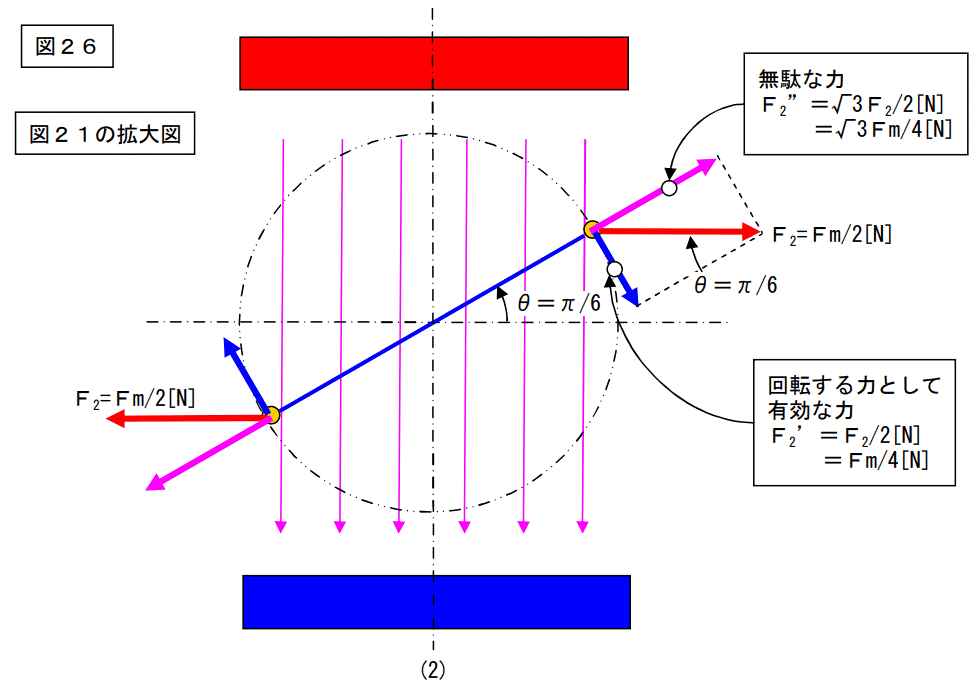
上図は(2)のポジションの場合を考えたものです。
この様に、回転に必要な力は発生していると考えることが出来ます。
因みにこの有効な力を表す計算式は下記になります。
F[N]=見かけの力×sin(ωt)
=2ωrsin(ωt)B2L2/R[N]×sin(ωt)
=2ωrsin2(ωt)B2L2/R[N]
=2ωr{BLsin(ωt)}2/R[N]
思いっきり訳の解らない式になりました。
多分あっていると思いますが、何処かで計算間違いをやらかしているかも知れません。
此処では、この計算式は余り重要ではありません。
「何故回るか?」が最重要項目です。
以上の記載で、誘導電動機が何故回るのかの話は終わりです。
実は、今まで記載した内容で、明らかなに「インチキ」の部分が有ります。
以下にその部分を記載します。
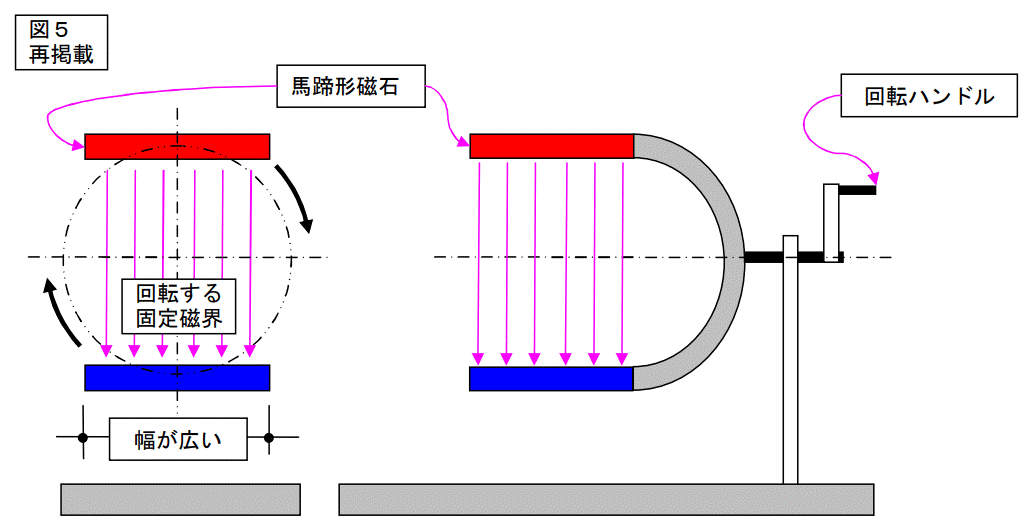
図5の磁束の分布ですが、馬蹄形磁石からはこんな磁束は出ません。
理解を得るために、敢えてインチキの図を描きました。
この図と同様な磁束分布を得るためには、下記のようなものが必要です。
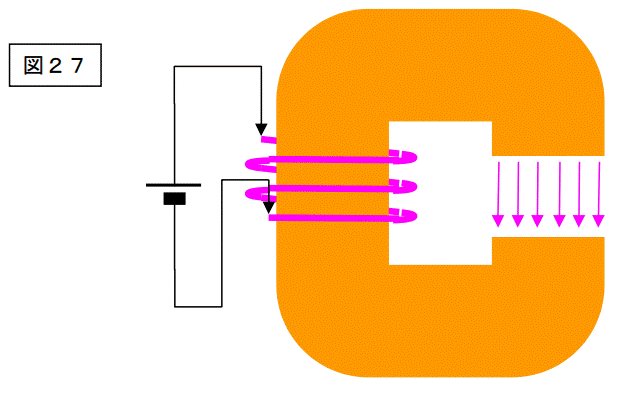
図5の磁束の幅ですが、幅が広いと書いてあります。
此処いら辺に、「集中巻き」では無く「分布巻き」にする必要性の、考えるヒントがあると思います。
図17の説明に下記の記載があります。
従って流れる電流は次の計算式で計算出来ます。
電流I[A]=電圧[V]÷抵抗[Ω]
=ωrBL[V]×2÷R[Ω]
これもインチキです。
導体のインピーダンスを抵抗のみで考えています。
しかし、実際はインダクタンス分が有ります。
この導体はリングの形をしています。
つまり、コイルです。
コイルに交流電流を流せば、インダクタンス分が発生します。
従って、この電流の計算式は正確ではありません。
とすると、今まで記載してきた導体が受ける力も違うことになります。
しかし、今回は此処まで突っ込むのはヤメにしています。
ワカンナイ! <==これが本音です。
最後に
馬蹄形磁石に跨っていたいた君!
もう用事は済んだから、降りても良いよ。
今回の講義はここでオシマイ
コメント