「誘導電動機は電圧を下げると電流が増える。」と言う話
皆様こんにちは
今回のお題は「誘導電動機は電圧を下げると電流が増える。」です。
電気屋の常識と反対の事態が起きるそうです。
この電動機の特性を知らなくても、使えれば良いのですが、知っていた方が何かと都合が良いので、この解説書(擬き?)を作りました。
皆様のご高覧を賜れば幸いです。

平成 鹿年 骨月 吉日
貧電工附属 埼玉ドズニーランド大学 学長 鹿の骨
早速ですが、下記の回路図をご覧下さい。
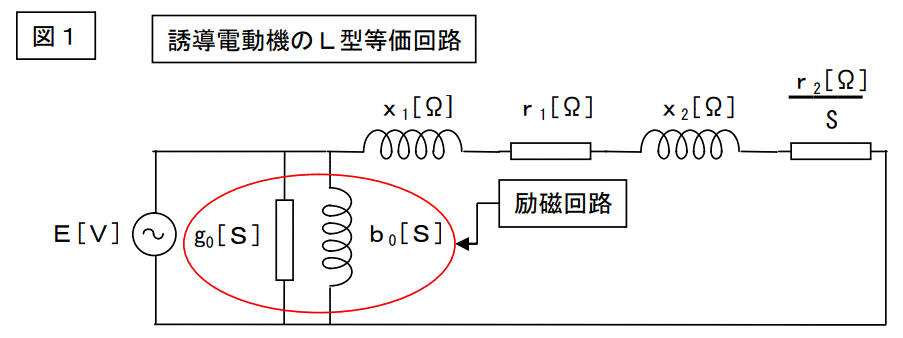
これは誘導電動機の「L型等価回路」と呼ばれるものです。
この等価回路がどうしてこの様な回路として描けるのかは説明しません。
「なるからなる。」として下さい。
「滑りと何ぞや」という説明もしません。
理解されていることを前提として話を進めます。この回路に現れている各数値(回路定数と言う。)を使って、計算式をコネクリ回すと、色々な事が解ることになっています。
ジャァ~という事で、計算式を立てようとすると、何処から手を付けて良いやらサッパリ解りません。
解析の仕方は色々あると思いますが、此処では次のような手法で解析を行います。
解析手法==> 「励磁回路を無視する。」
早い話、等価回路を下記のように描き直して解析をスタートします。尚、解析に当たって、特に断らない限り、電動機は2極機とし、等価回路は三相の一相分のみを描きます。
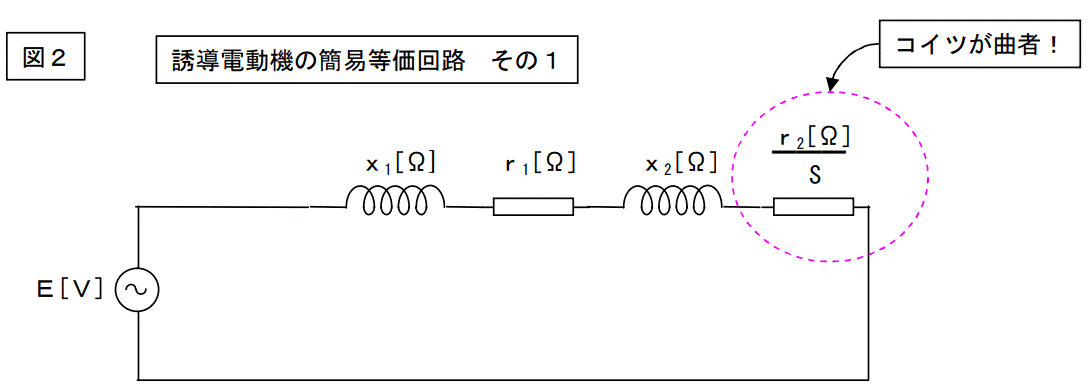
コレを元に数式をこねくり回して見ましょう。
と言うことで鹿の骨流、半分インチキ講座の始まり始まり・・・。
さらにこの図を下図のように変形します。
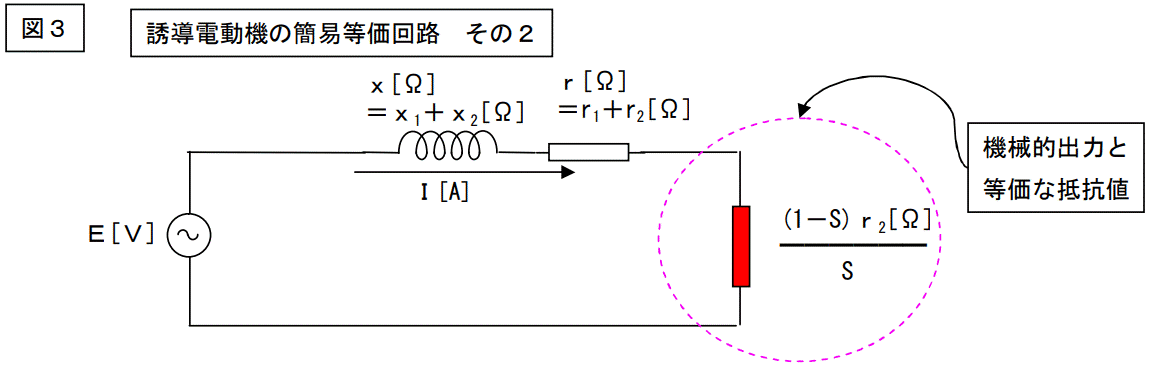

何やら小難しい式になりました。
電流値が取り敢えず解りましたので、この電動機の機械的出力を計算してみましょう。
機械的出力=機械的出力と等価の抵抗器が消費する電力=機械的出力と等価の抵抗器の抵抗値×電流の2乗(早い話、I2Rです。)
機械的出力をPm と置くと

これも何だか良く解らない数式になりました。
①式の電流の式、②式の出力の式、何れも良く解らない式です。
数式をジッと眺めていても何も解りません。
そこで、等価回路をもっと簡略化してみました。
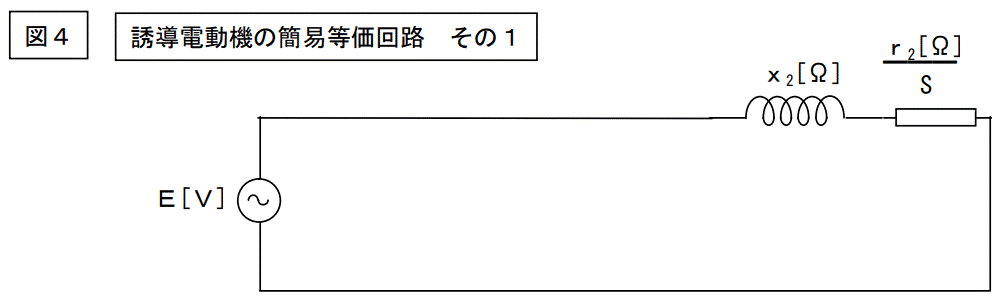
この様な回路にしてみました。
この回路は励磁回路を無視し、さらに・・・。
解析手法その2==> 「一次側の回路定数を無視する。」
と言うものです。。
恐ろしく簡単な回路図になりました。
コレだったら何とかなるだろうと言うことで次に行きます。
さらにこの図を下図のように変形します。
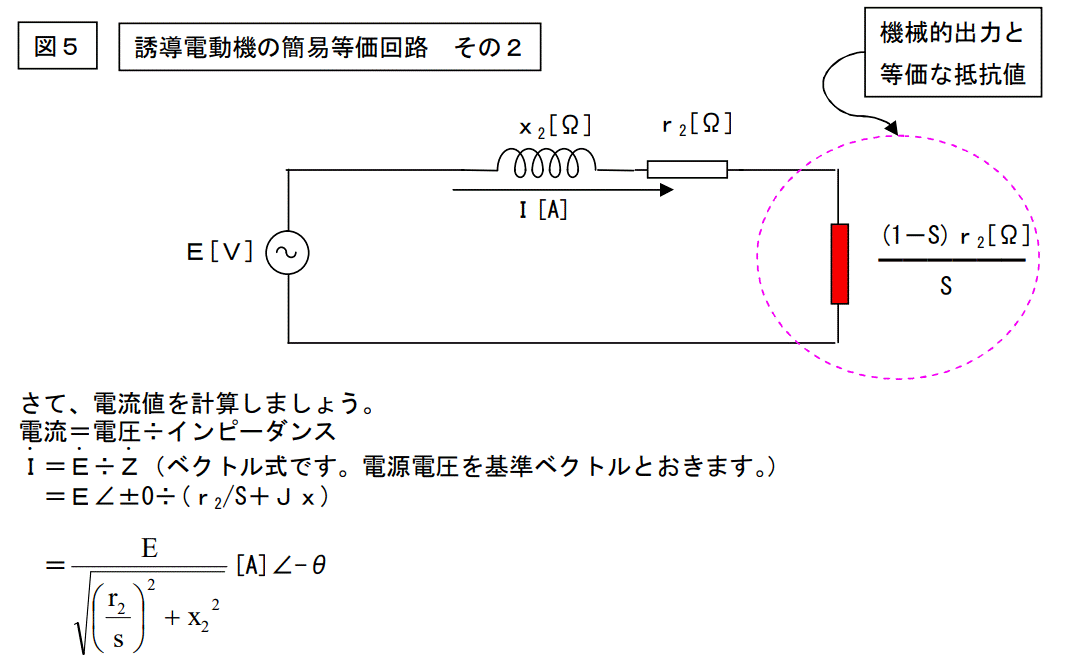
電流値が解りましたので、次は電動機の機械的出力です。
機械的出力=機械的出力と等価の抵抗器が消費する電力
=機械的出力と等価の抵抗器の抵抗値×電流の2乗
機械的出力をPm と置くと
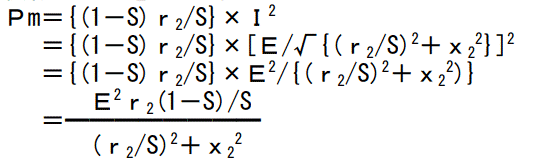
これも何だか簡単なのか難しいのか良く解らない式です。
困った・・・そこで、次ページの様な事を考えます。
苦し紛れに図5の等価回路をさらに下図のように変形します。
どうなってしまうのか・・・?
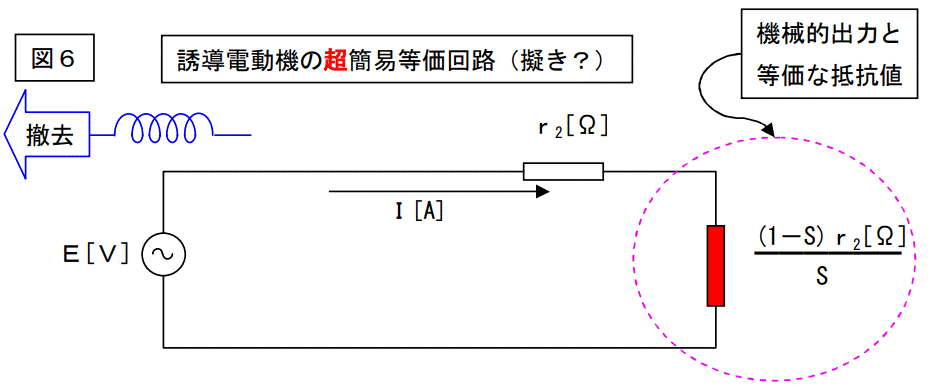
図5の漏れインダクタンスxを撤去しました。
此処まで簡略化すると、等価回路と言えるかどうか怪しい事になりますが、取り敢えずこれで再計算をしてみましょう。
ナンジャコリャ?

となりますので、軸出力は出ません。
つまり、誘導電動機は同期回転では回りません。
今度は S=1を代入して見ましょう。
Pm=-aS2+aS
=-a12+a1
=0[W]
やはり、軸出力は出ません。
始動直後ですから、回転子は回っていません。ですから出力はゼロです。
では S が0~1の中間値を取った場合はどうなるのでしょうか?

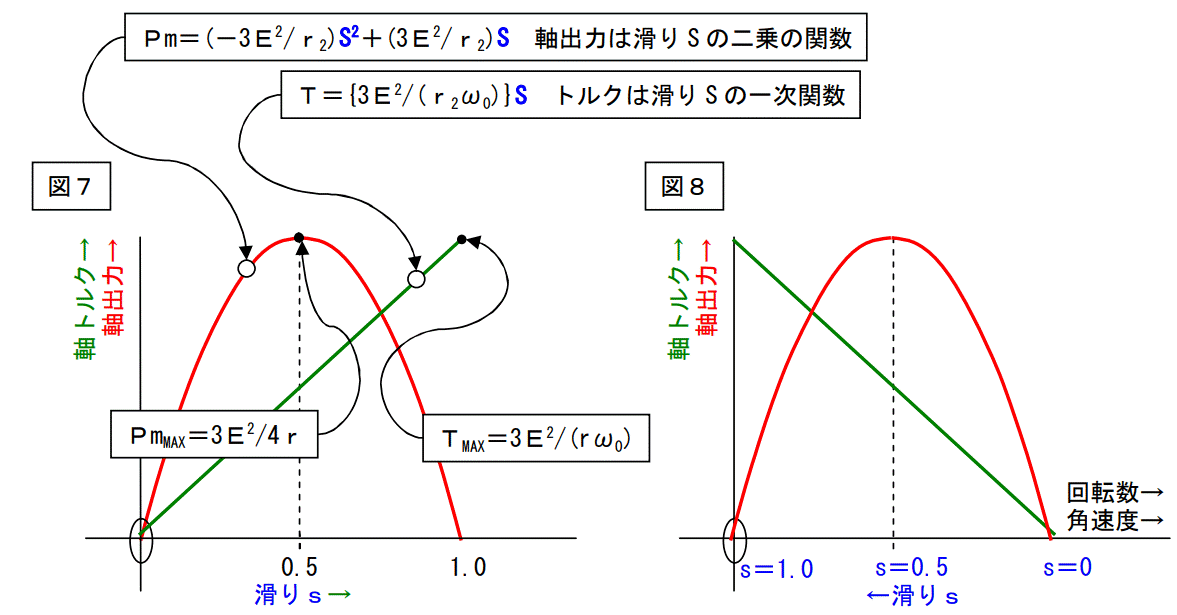
一般的には横軸に回転数又は角速度を取りますので、図が左右反転されて図8の様になります。
此処で電圧と電流の関係を見てみましょう。
電圧が変わったら、電流はどうなるか?です。
電気の常識からすると、一般的に電圧を上げれば電流は多くなり、下げれば少なくなります。
さてどの様な結果になるのでしょうか・・・。
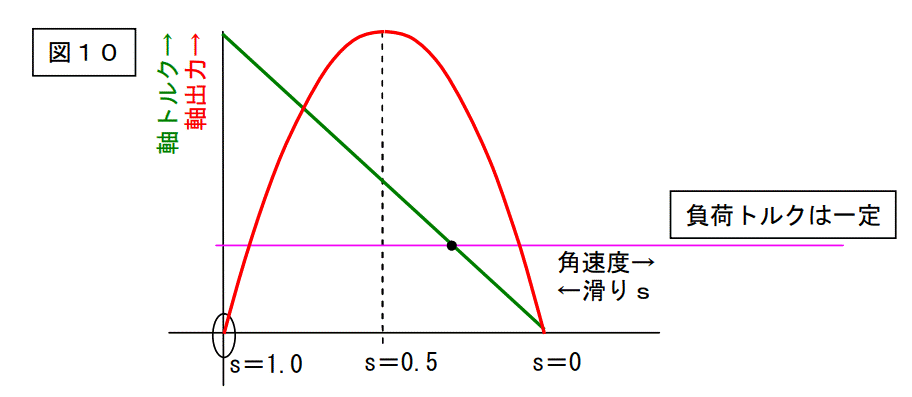
前提条件として、負荷が要求するトルクは一定とします。
下図参照。

でもねぇ~・・・
この話はインチキなんですよ。ハイ!
元の等価回路がインチキだから・・・
インチキがバレバレの話ですが、もう少し補足します。
実はこのインチキ話、最後の方に行くと、USO800では無く、USO80位の話になります。
ですから、この胡散臭い話を確実に理解して下さい。
さて、トルクの式は下記でした。
T={3E2/(r2ω0)}S[N・m]
この式は前述の様に S の関数ですが、電圧Eを変化させた場合は、Eの関数にもなります。
Eの2乗の式になっていますから、トルクは電圧の2乗に比例します。
電圧を 1.2 倍にすれば、トルクは 1.14 倍になり、0.8 倍にすれば、0.64 倍になります。
軸出力も同様に、Pm=3E2
(1-S)S/r2[W]でしたから、軸出力も電圧の2乗に比例します。
下図参照。
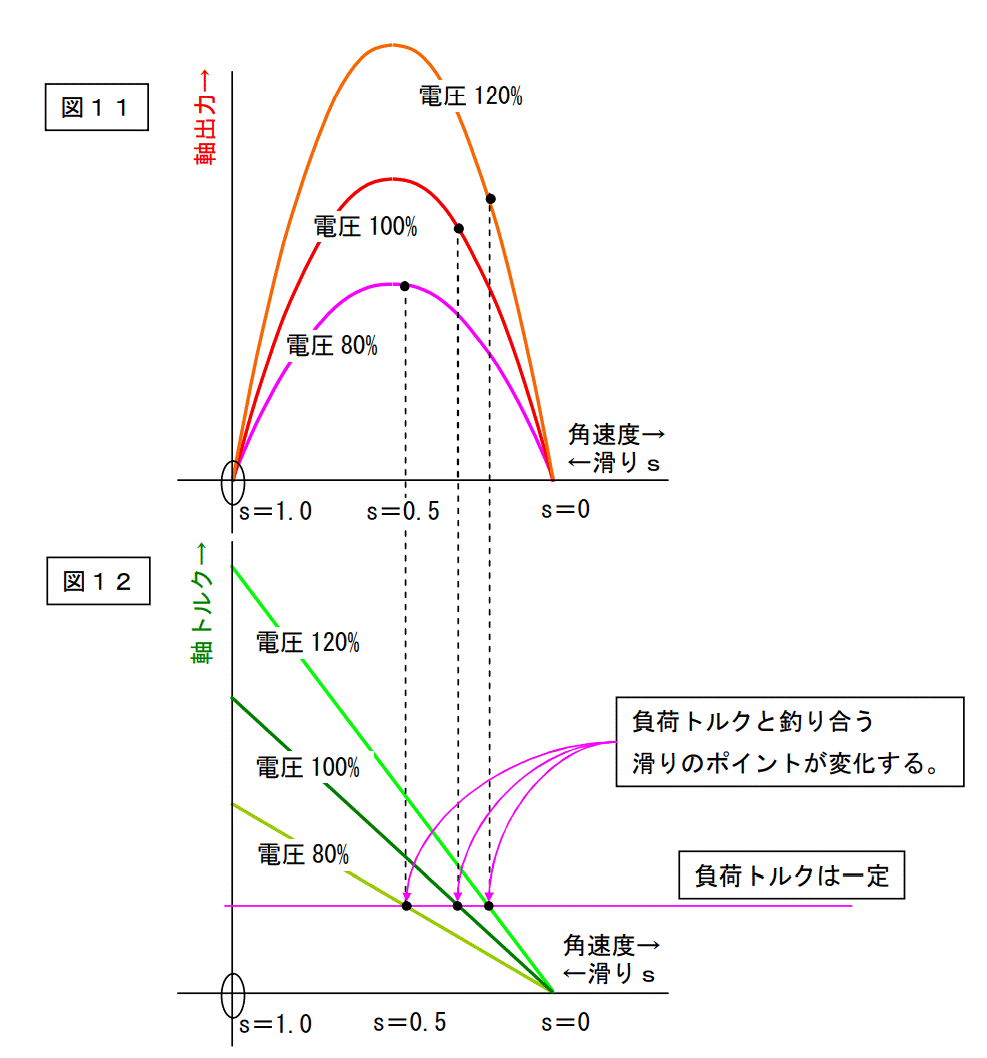
この様に、電圧を変化させた場合、トルクが一定を条件とすると、負荷トルクと釣り合う(回転を維持する)滑りの値が、勝手に変わります。
電動機はトルクを一定に保つ為に、電圧が上がれば滑りを減少させ(早く回る。)、下がれば滑りを増やします(遅く回る。)。
さて、等価回路擬きの解説はこの位にして、本来の等価回路の解説に戻りましょう。
1ページの図2及び2ページの図3の解析に移ります。
2ページで2つの式が得られていました。
電流Iの式
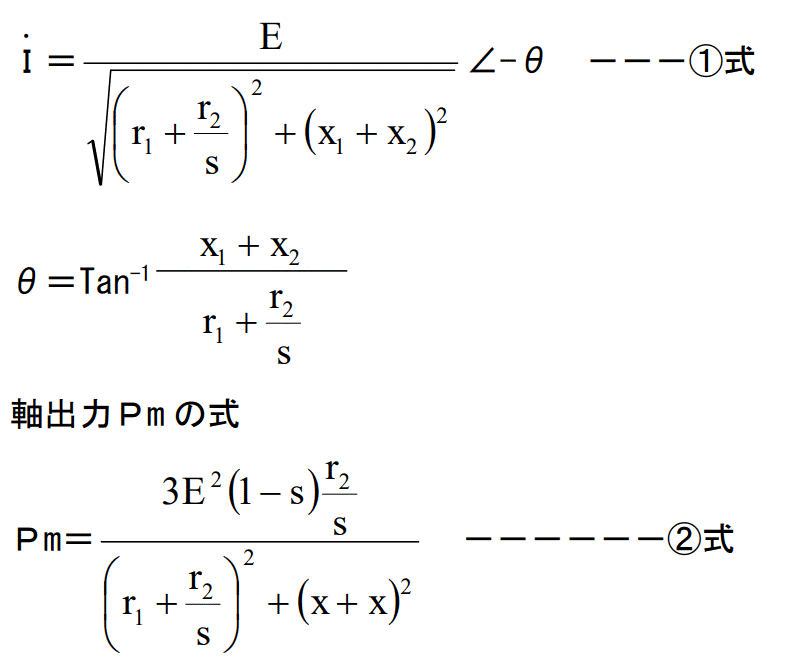
トルクの式が得られていませんので計算します。
トルクの計算を行う為には、角速度が必要ですが、角速度は、同期角速度をω0 と置くと下記のようになります。
滑り S の時の角速度ωS=ω0(1-S) ---③式
この式を使って、トルクを計算します。
トルクT=軸出力Pm÷角速度ωS
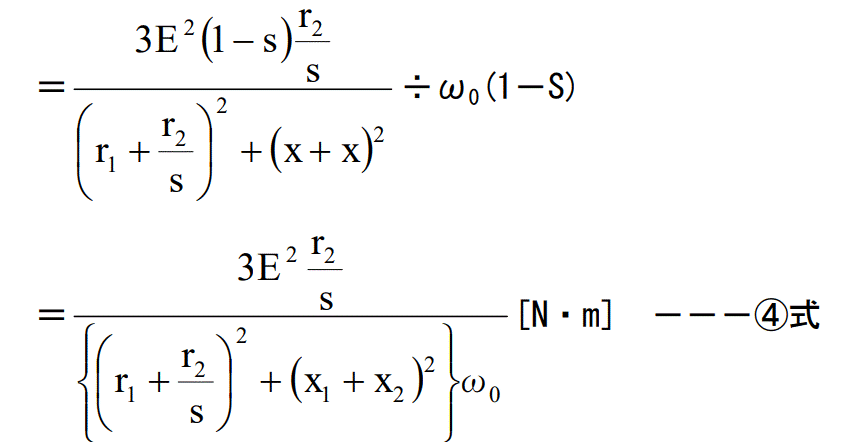
これらの式は、何回見ても難解な式です。(オヤジギャグをかましている場合では無いが・・・。)
ですから、これらの式の内容を理解するのには別の手法を考えます。
別の解析手法==>パソコンに計算させ、グラフを書かせる。
①~④式はワケのワカラン式ですが、パソコンに計算させれば、どんなに難しい式でも関係有りません。パソコンに計算させる時の条件として、滑りSだけが変数で、他は定数とします。
一次導体抵抗 r1、二次導体抵抗 r2、一次漏れリアクタンスx1、二次漏れリアクタンスx2、電源電圧E、これらは全部定数とします。
滑りは0(同期回転で回転)~1(始動時)の範囲で変化します。
ですから、滑りが0~1の間で変化するときに、電流、出力、トルクがどの様な値になるのかを検討します。
コンピュータは実値を与えないと計算してくれませんから、実値は下記のように設定します。
r1=0.3[Ω]
r2=0.3[Ω]
x1=0.8[Ω]
x2=0.4[Ω]
E=200/√3[V]
Eの値以外はハッキリ言って適当な値です。
世の中にこんな値の誘導電動機が有るのか無いのか・・・知るか!
まことしやかな数値を入れただけだよょ~ん!!
手始めに、コンピュータに「滑りと電流値との関係」をグラフ化させると下図のようなグラフを書いてくれました。
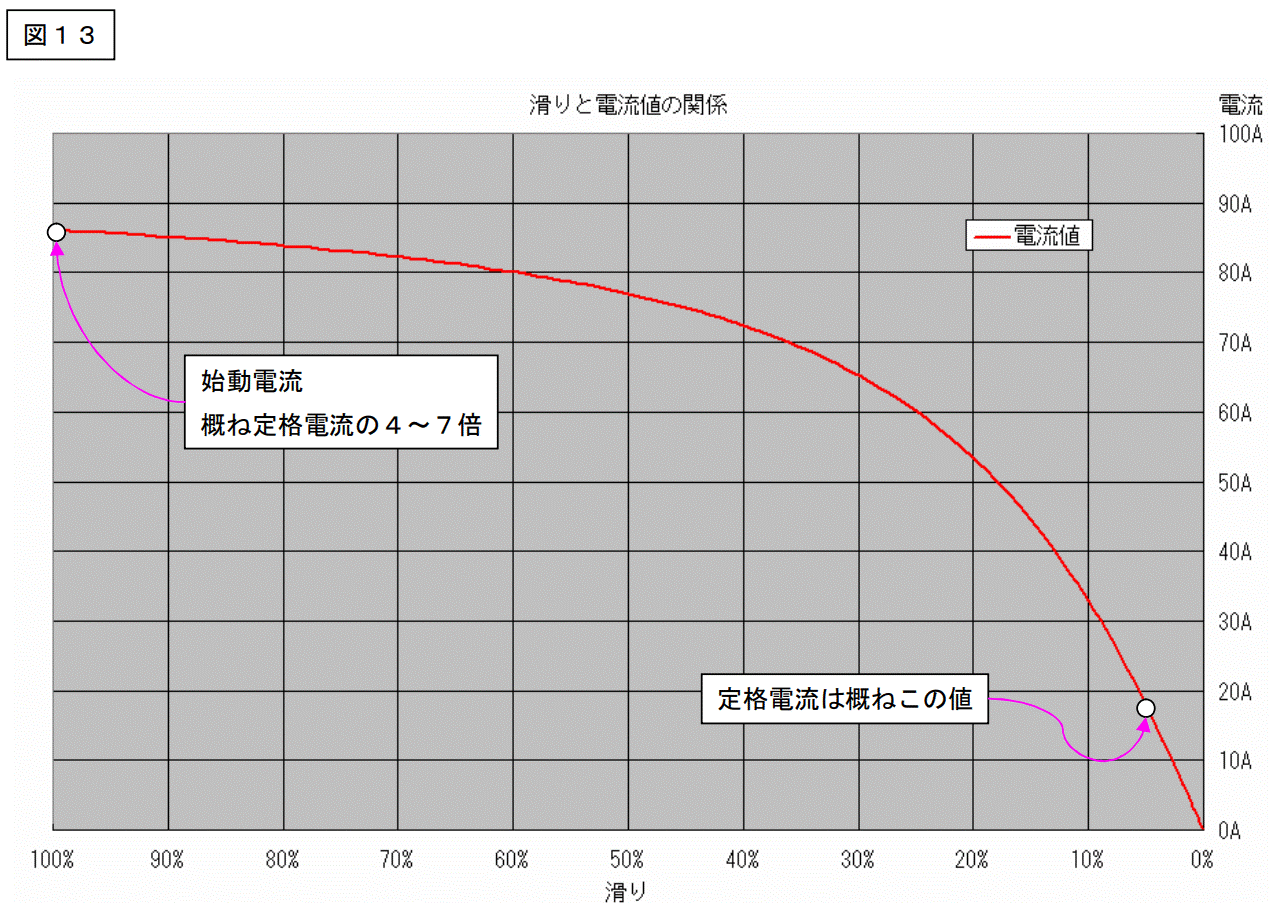
グラフは横軸に滑り、縦軸に電流値を置いています。
滑りの値は右側に行くに従って小さくなります。(回転数は右側に行くに従って大きくなります。)
このグラフを見ると次のような事が解ります。
1.電流値は始動時が最大(滑り=100%、回転数=ゼロ)
2.滑りが小さくなるに従って、電流値は小さくなる。(回転数が上がるに従って電流値は小さくなる。)
3.同期回転数では電流は流れない。
どうしてこの様なグラフになるのかは、コンピュータに聞いて下さい。
S=1.00、0.99、098・・・0.01 と代入して計算した結果が上記のグラフです。
とにかく「なるからなる。」としか言いようがありません。
尚、グラフの電流値は位相を無視しています。
次ページに今度は軸出力のグラフを記載します。
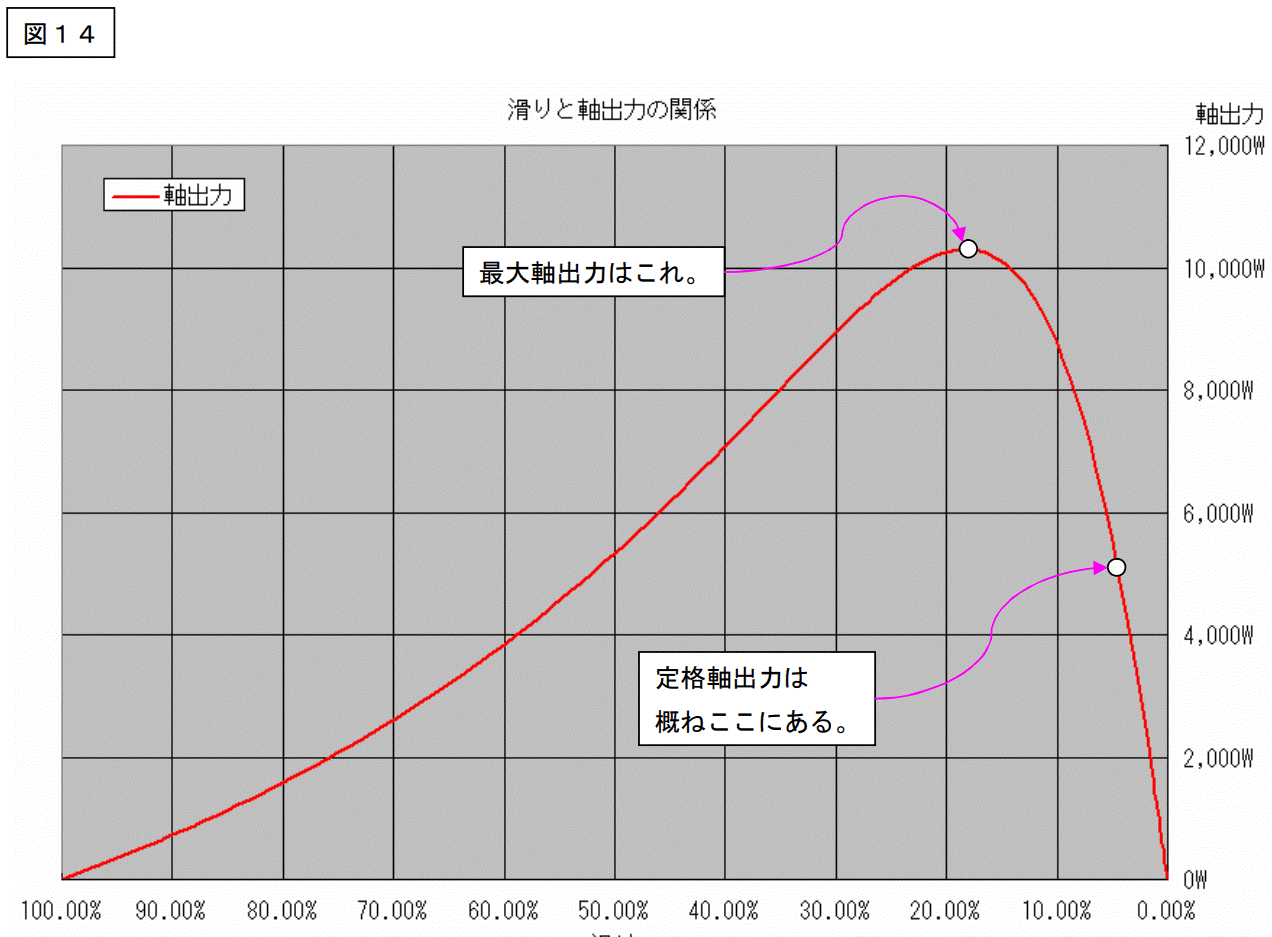
グラフは横軸に滑り、縦軸に軸出力値を置いています。
このグラフを見ると次のような事が解ります。
1.軸出力値は始動時にはゼロ。
回っていないので出力=0は当たり前の事です。
2.滑り=0%、つまり同期回転の時は、軸出力はゼロになる。
軸出力、トルク、角速度の関係は下記です。
軸出力[W]=トルク[N・m]×角速度[rad/秒](<==回転力学の公式です。)
つまり、同期回転時にはトルクがゼロになっていることが解ります。
結果として、誘導電動機は同期回転では絶対に回りません。
必ず滑りを伴って、同期回転数より遅い回転で回ります。
3.最大出力は、始動~同期回転の中間に有る。
この図では概ね、滑り=20%付近で最大出力が出ます。
通常の定格滑りは3~6%程度ですから、最大軸出力は概ね定格値の2倍程度であることも解ります。
この値は、回路定数を変化させると大きく変わります。
ですから、何時も2倍と言うわけではありませんし、最大値の発生滑りが20%付近とも限りません。
後の方で、色々値を変えてやってみます。
次ページはトルクです。
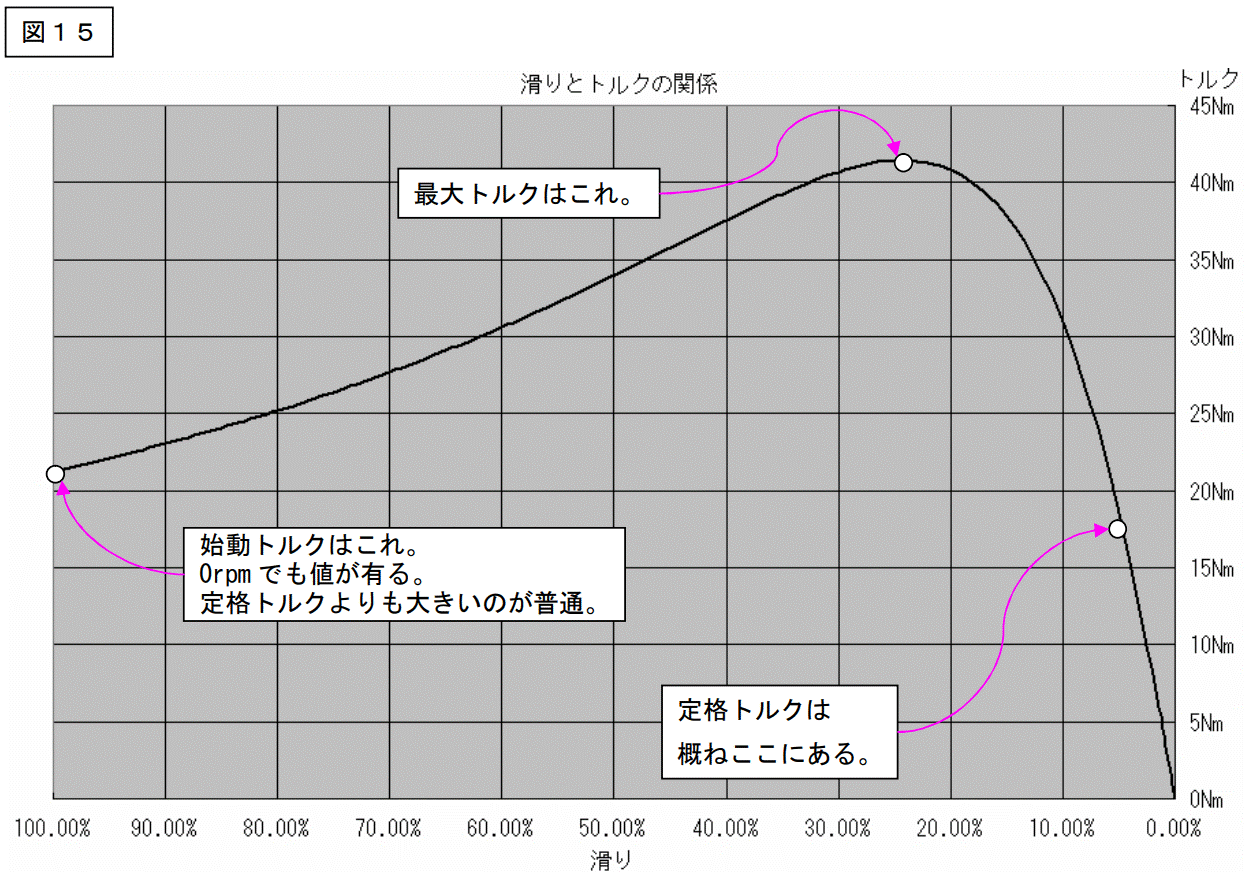
4ページに記載した軸出力のグラフと似たようなグラフになります。
同期回転数ではトルクはゼロです。軸出力もゼロです。
トルクは0[rpm]つまり、始動時にも値を持ちます。(滑り s=1 の時)
④式に s=1 を代入すると始動トルクの式を得ることが出来ます。
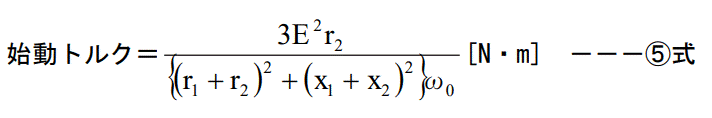
ついでと言っては何ですが、コンピュータは色々な計算をやってくれます。
ですから、消費電力と力率の計算もやってみました。
結果を下記に示します。
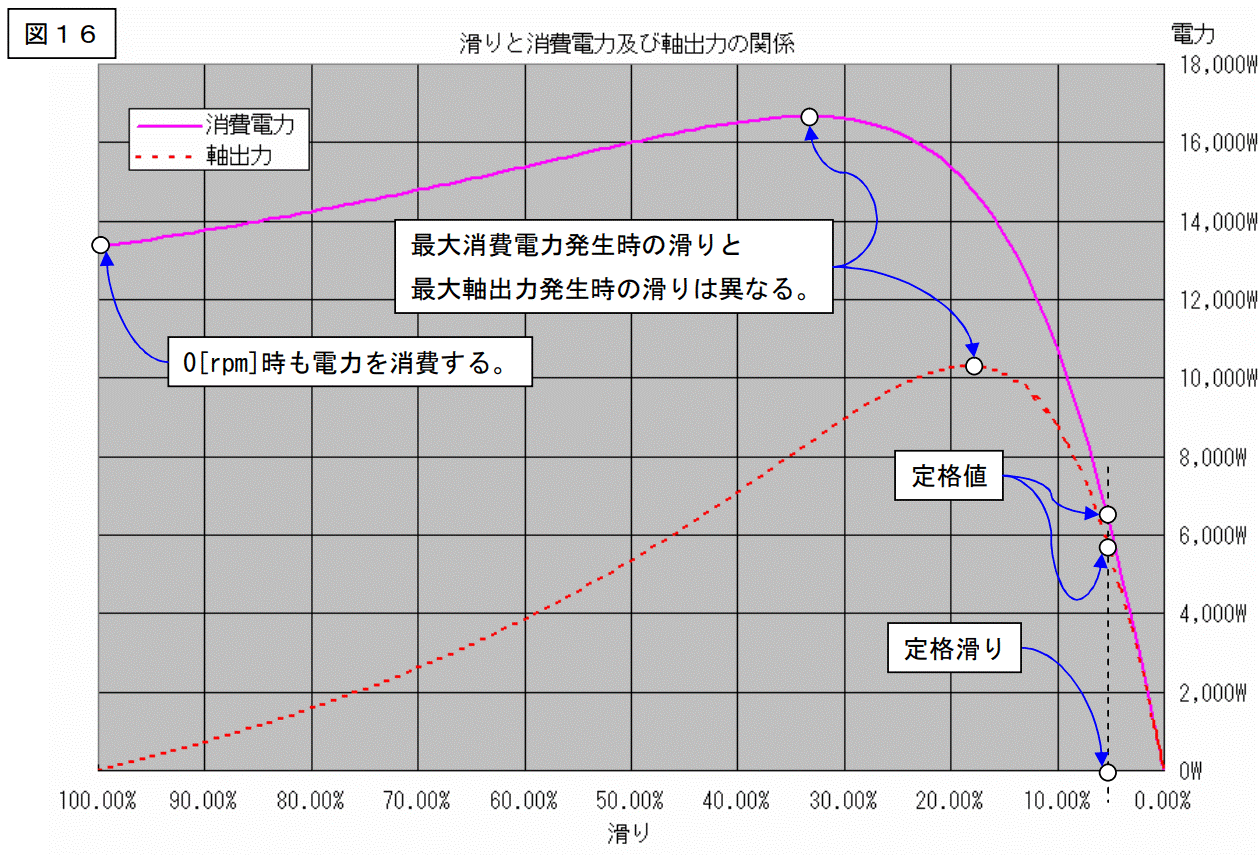
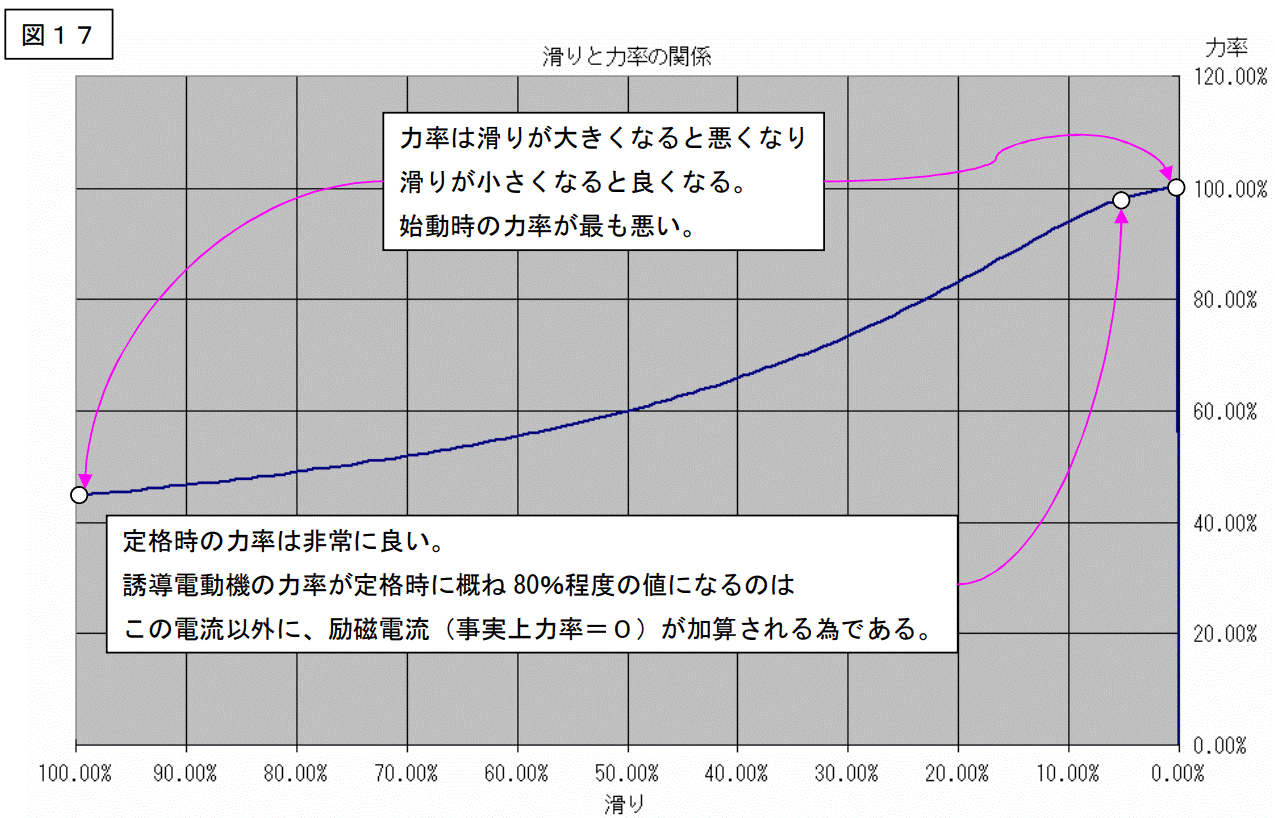
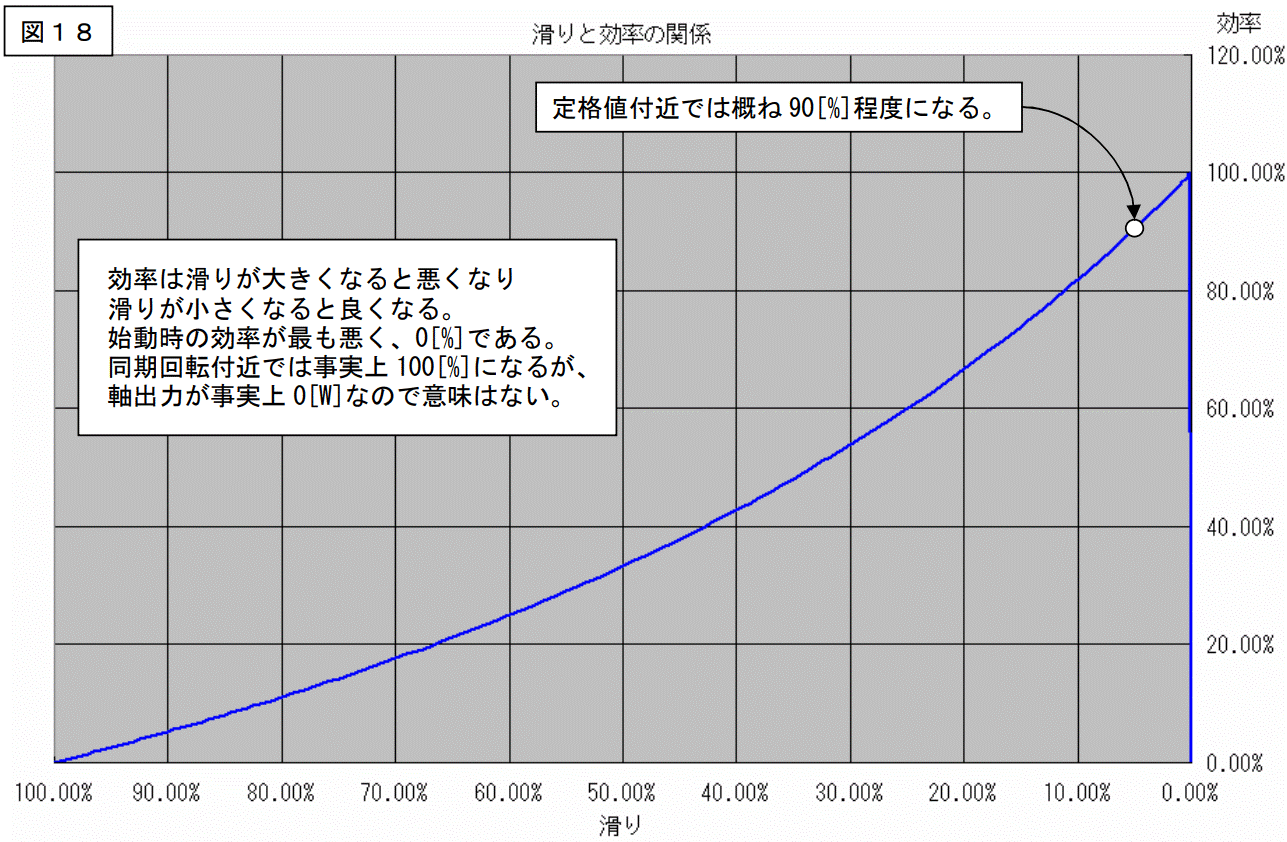
効率の計算もやってみました。
結果を下記に示します。
ここで、定格値の話を書きます。
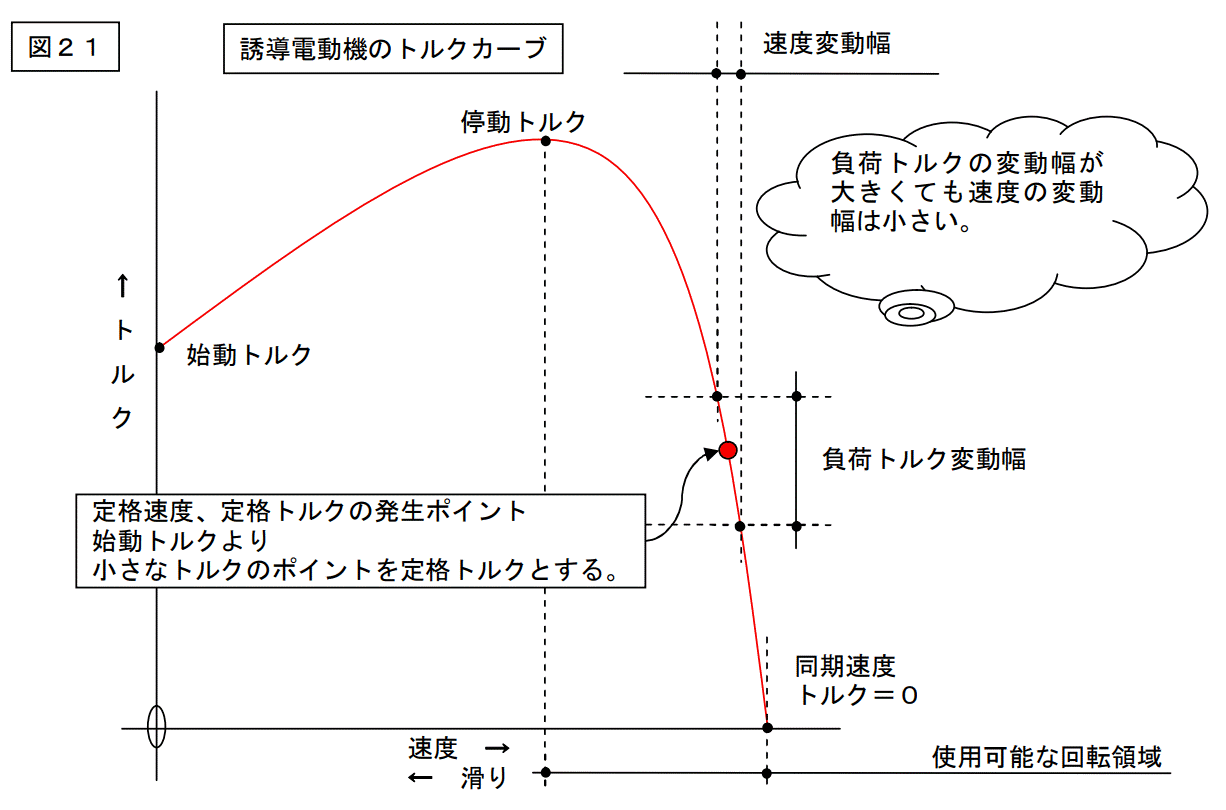
誘導電動機の特性で、説明しなければならないことは沢山ありますが、まず定格値です。
今まで書いてきた各特性の中で「定格値」が出てきますが、何れもが滑り=約5%の所の値です。
滑りは 100%~0%まで変化しますが、何故5%程度の所で使うのかと言う話です。
これはトルクを使って説明します。
下図はトルクの特性及び使用可能回転域の図です。
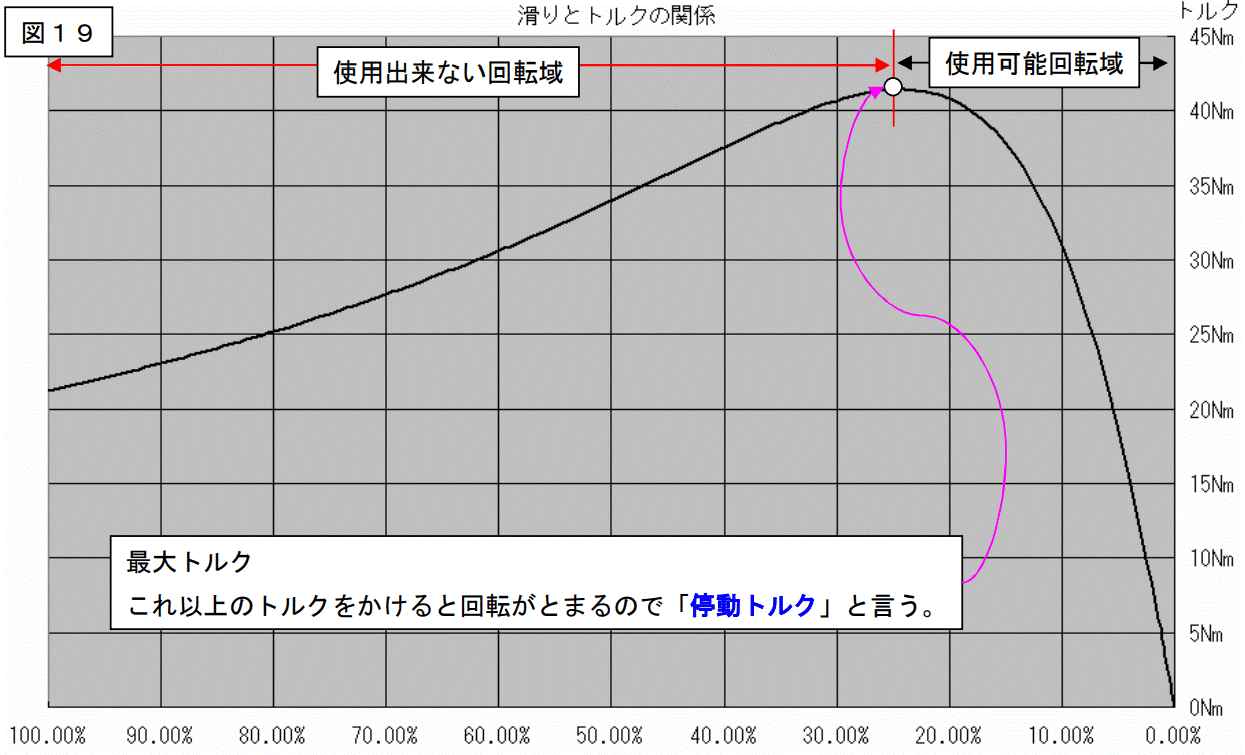
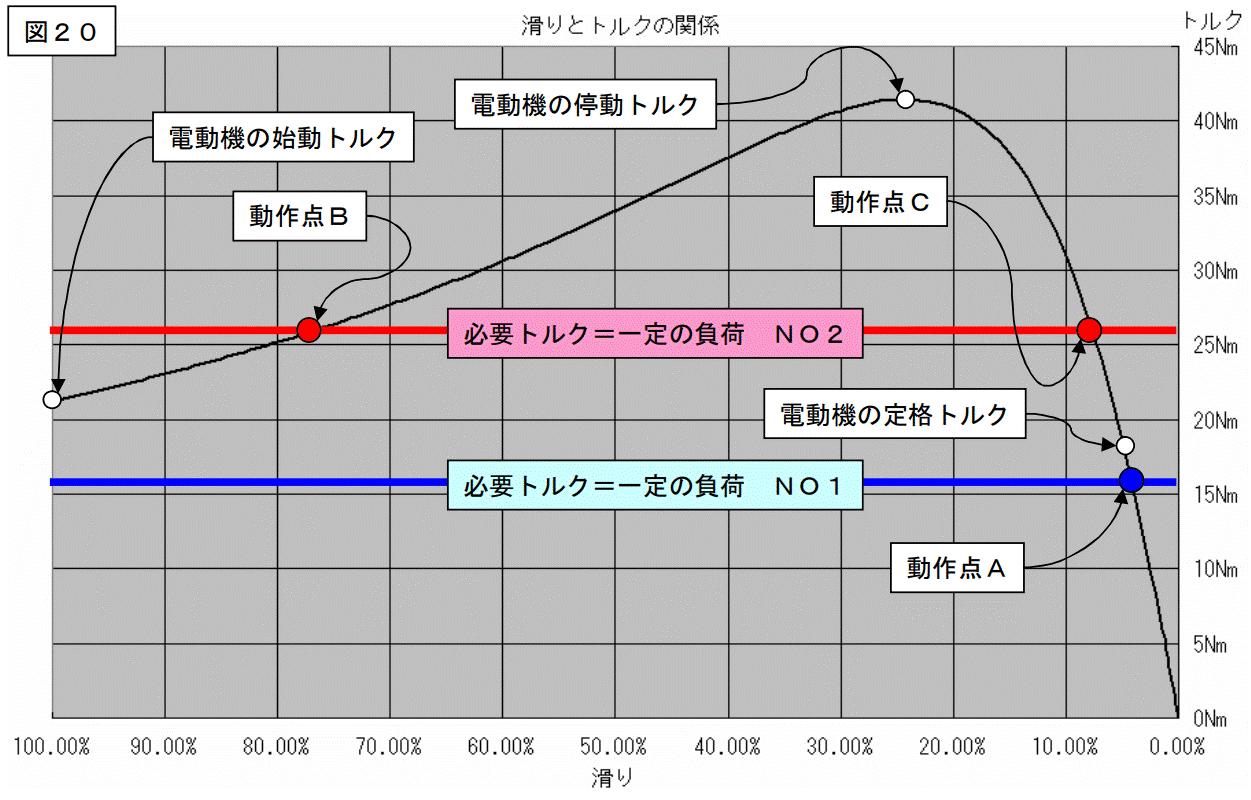
下図のようなトルク特性を持った負荷が2つ有ったとします。
「定トルク負荷」と言いますが、ベルトコンベアなどがこれに該当します。
まず電動機が「回る」「回らない」の話から始めます。
電動機が回るか回らないかの判定は下記です。
「負荷トルク<電動機軸出力トルク」の場合、電動機は加速します。
「負荷トルク=電動機軸出力トルク」の場合、電動機はその時点での角速度を維持します。
「負荷トルク>電動機軸出力トルク」の場合、電動機は減速します。
この様に、負荷トルクと電動機軸出力トルクの関係が「<」、「=」、「>」の何れになっているかで判定出来ます。
つまり、電動機が回る条件は「負荷トルク≦電動機軸出力トルク」です。
上図のNO1の場合から説明します。
まず始動時ですが、図の様に負荷が必要としているトルクより、始動トルクの方が大きい値を持っています。従って、この負荷の場合、電動機は始動出来ます。
始動した後は、電動機の発生するトルクが、負荷の要求するトルクを上回っていますから、電動機は加速します。
途中で加速を止めさせたいと思っても、情け容赦なく電動機は加速を続けます。ドンドン加速して、停動トルクの回転を過ぎても、未だ発生トルクの方が負荷のトルクより大きな値になっていますから加速はとまりません。
定格トルク発生回転数を過ぎて、「動作点A」まで来て、此処で加速が止まり、回転が安定します。
つまり、始動(回転数=0)~停動トルク発生回転までは使おうと思っても、使えない回転数になります。
ソレジャァと言うことで、今度はNO2の負荷を持ってきます。始動時は、負荷の要求するトルクより始動トルクの方が小さいので、このままでは電動機は始動出来ません。
仕方が無いので、補助電動機を接続して、始動時のみトルクを加算します。(実務でこんな事はやらない。)そうすると、取り敢えず始動することができます。
電動機を加速させ、「動作点B」の回転数まで来た時に、補助電動機を切り離して、この電動機の単独運転に切り換えたとします。
さて、この電動機は「動作点B」で回転数を一定に保ってくれるでしょうか?
残念ながら、そう旨く話は進みません。
この回転数まで回転が上昇し、電動機の発生トルクが負荷の要求するトルクを上回る事が出来るようになると、電動機は加速してしまいます。「頼むからそこで加速をヤメテクレ。」と思っても、電動機は加速します。
ドンドン加速して、「動作点C」まで回転数が上がって、この時点でやっと加速が止まります。
以上の様な話をまとめると下図の様になります。
動作点A又は動作点Cの回転数で回っている時に負荷が暴れてトルクが変動した場合、
「負荷トルクが増えてしまった場合、回転数は落ちるがトルクが増えるので回転落ちは少ない。」
「負荷トルクが減ってしまった場合、回転数は早くなるがトルクが減るので回転上昇は少ない。」
と言う具合に自動的に制御がかかります。
この様に、誘導電動機は停動トルク発生回転数~同期回転数までが使用可能回転域となり、回転特性は「事実上の定回転電動機」となります。
この様に「定格値」は同期回転よりもホンの少し遅い回転数で設定することになります。
つまり、定格滑りは数%です。 <==実はこれが非常に重要!!
定格の滑りが数十%の電動機もあると思いますが、汎用機の場合3~6%程度で使用するのが普通です。
又、回転数(=滑り)を決めているのはトルクです。軸出力では有りません。
軸出力トルクと負荷トルクが釣り合った回転数で電動機は回ります。最初にトルクが決まり、結果として出力が決まります。誘導電動機の話をするときは「トルクが要」となります。
さて、これらの特性が得られましたので今度は、固定だった電圧を変化させた場合、どの様な変化が起きるのかを見てみましょう。
まずは電流値です。
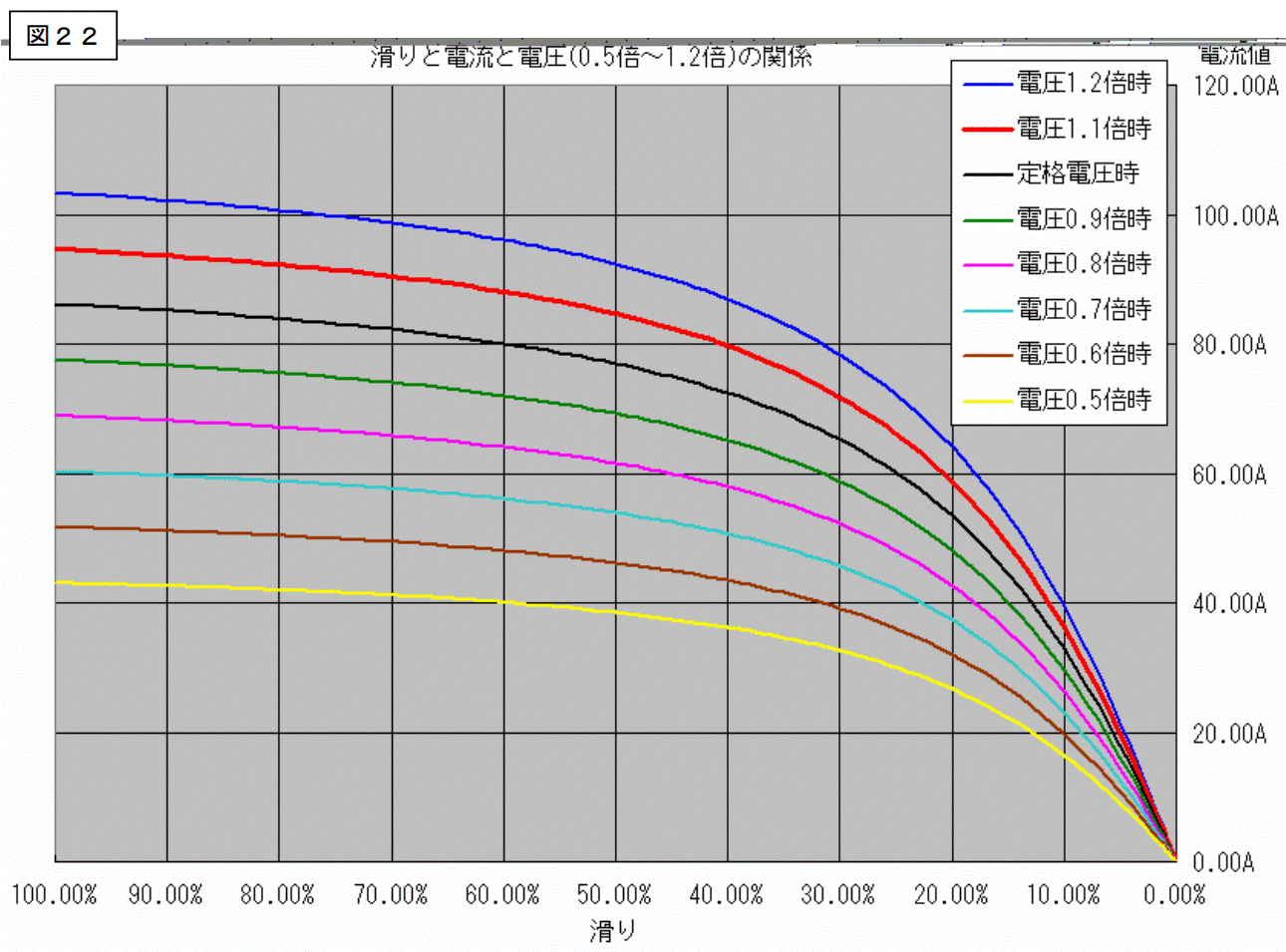
電圧を色々変えると、上図のような結果が得られました。
このグラフを見ると次のことが言えます。
電圧を変化させた場合、滑りが同じであれば、電流は電圧に比例する。
この結論は「電圧と電流は反比例する。」という話と全く反対の結論になっています。
実は、この結論に矛盾は無いのです。
滑りが同じで有れば、と言う条件が付いていることに注意して下さい。
負荷を背負って回っている電動機の電圧を下げた場合、下げる前と下げた後では滑りが異なります。
後の方で、この特性は詳しく説明しますが、滑りが変わってしまいますので、滑りが同じという条件が崩れます。
電圧を下げれば電流も下がると単純に考えてはイケマセン。この電流と電圧の関係は「始動時」に適用することが多いと思います。始動時は滑り=100%ですから、電圧が高い場合と低い場合も滑りが同じです。
従って、始動時に電圧を下げれば、始動電流(滑り=100%の時の電流)を下げることが出来ます。
これが、スターデルタ始動やリアクトル始動の原理です。電圧を半分にすれば、始動電流は半分になり、1/3にすれば1/3になります。
次ページは軸出力です。
軸出力です。
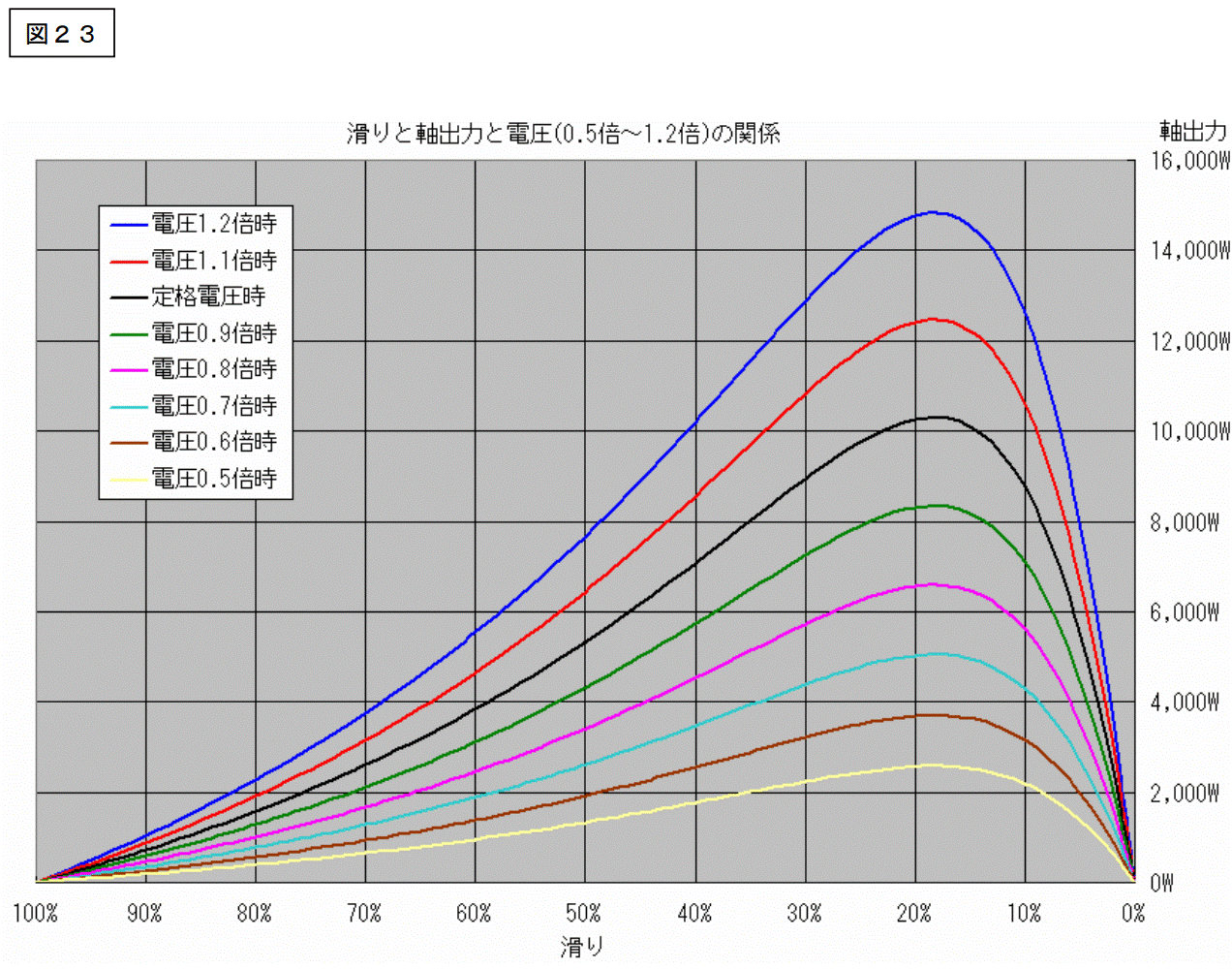
このグラフを見ると次のことが言えます。
電圧を変化させた場合、滑りが同じであれば、軸出力は電圧の2乗に比例する。
このグラフを読むときの注意点は電流の場合と同じです。
「滑りが同じで有れば」という所に注意して下さい。
次ページはトルクです。
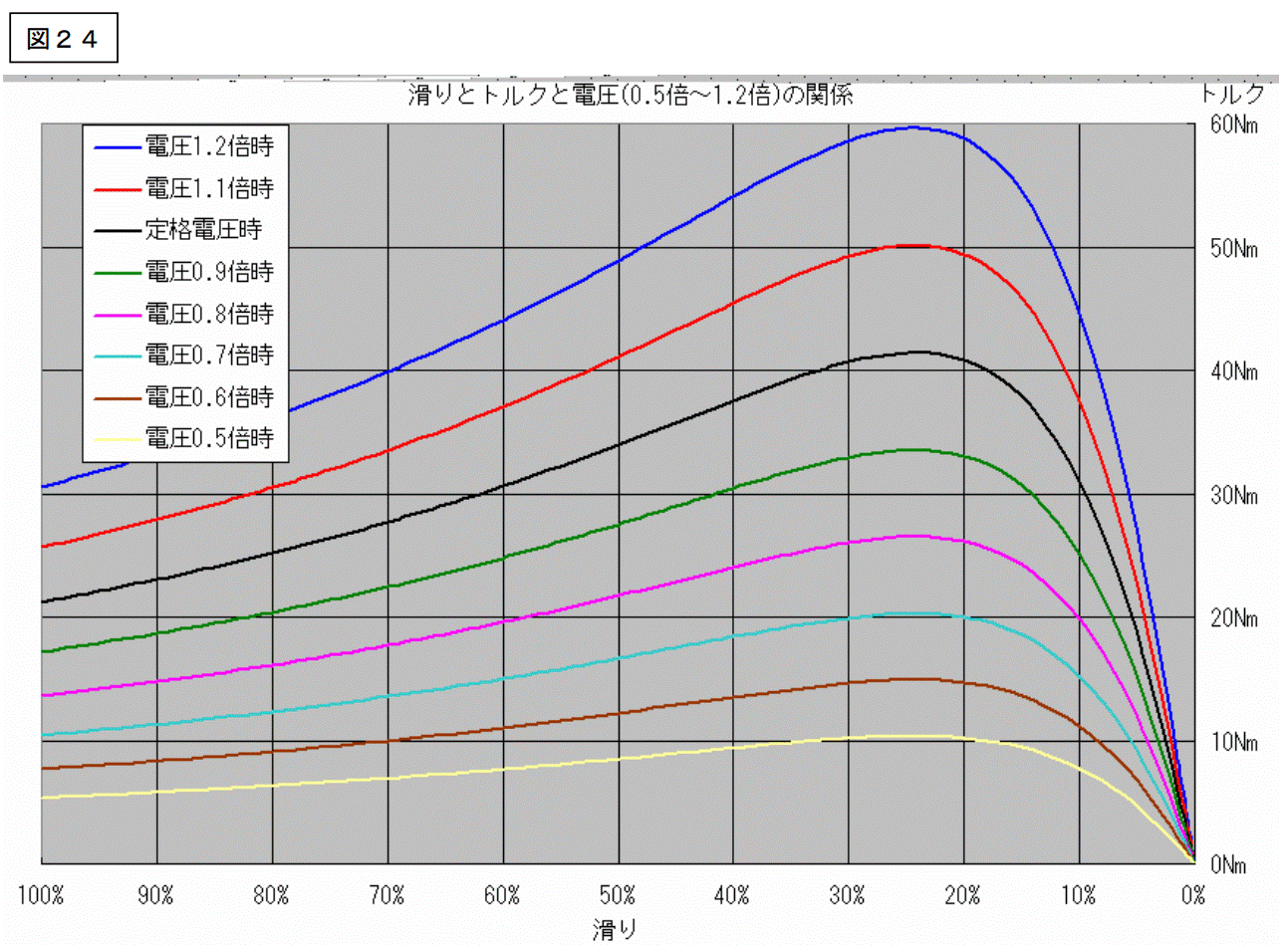
このグラフを見ると次のことが言えます。
電圧を変化させた場合、滑りが同じであれば、トルクは電圧の2乗に比例する。
このグラフを読むときの注意点は前の場合と同じです。
「滑りが同じで有れば」という所に注意して下さい。
次ページは消費電力と力率と効率です。
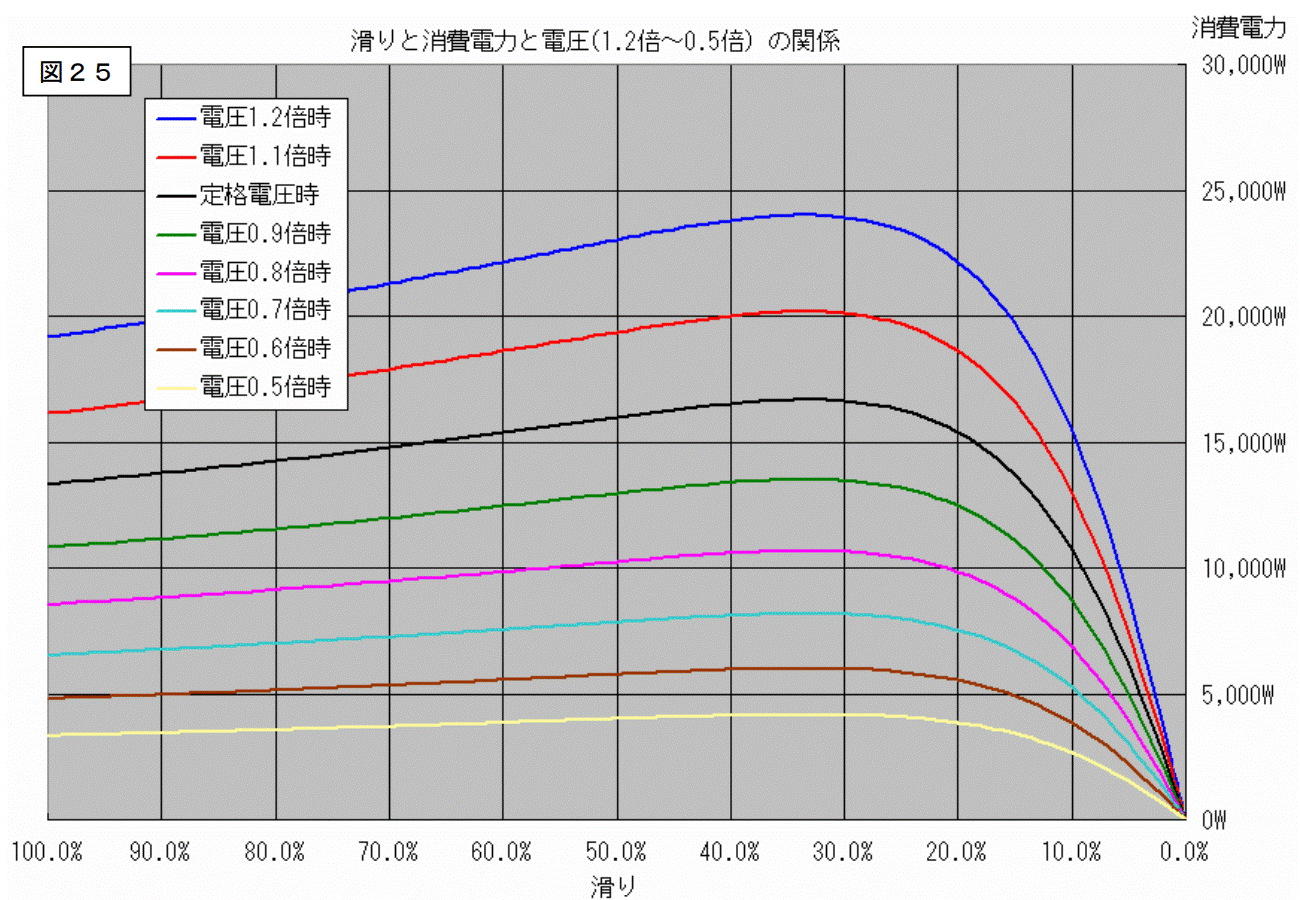
電圧を変化させた場合、滑りが同じであれば、消費電力は電圧の2乗に比例する。
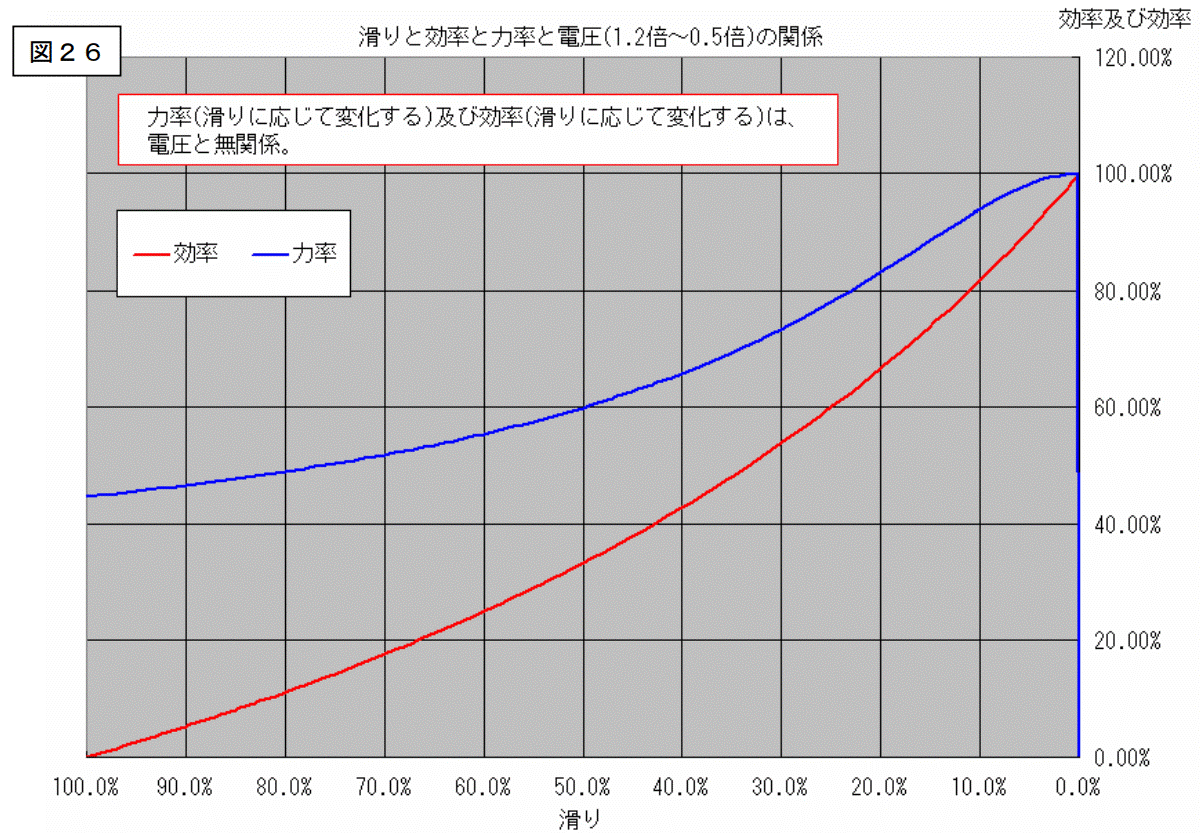
以上で取り敢えず電圧を変化させた場合の説明は終わりです。
電圧を変化させた場合の特性は何となく理解出来たと思うのですが、負荷がかかった状態で、電圧を変化させた場合、電流値がどうなるかがいまいちピンと来ません。
此処いら辺を説明します。
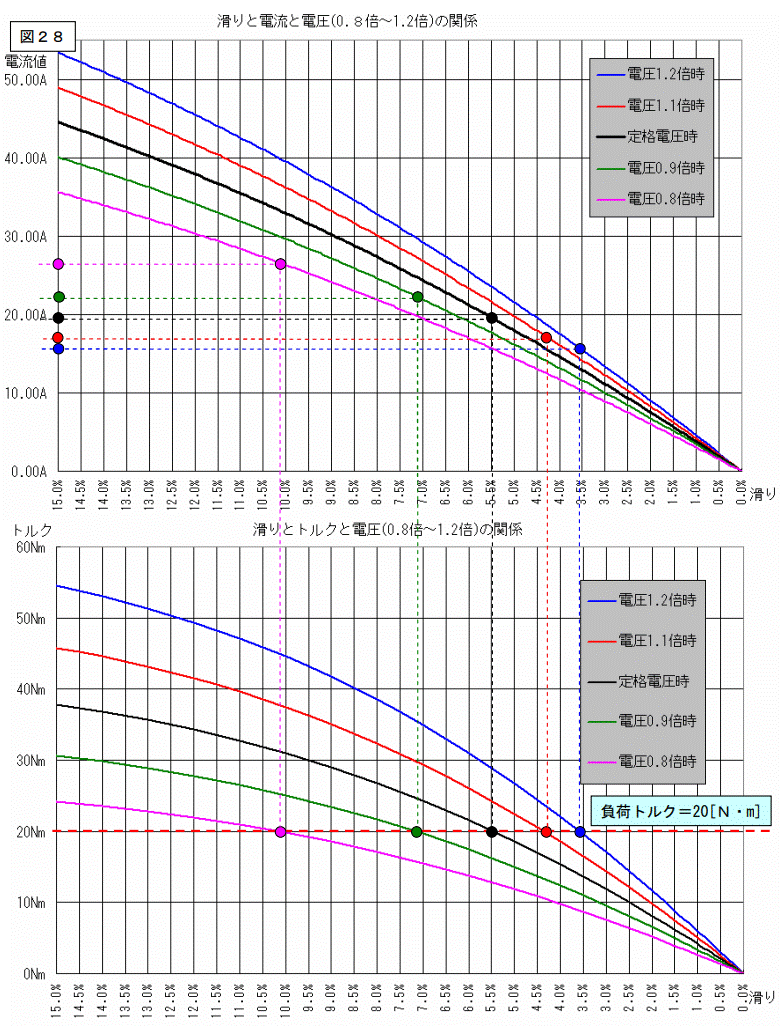
各値に滑りが非常に大きな影響を持つことはご理解されたいると思いますが、この滑りを決める(=回転数を決める)トルクの話から始めます。前述と同様に、負荷トルクは一定とします。
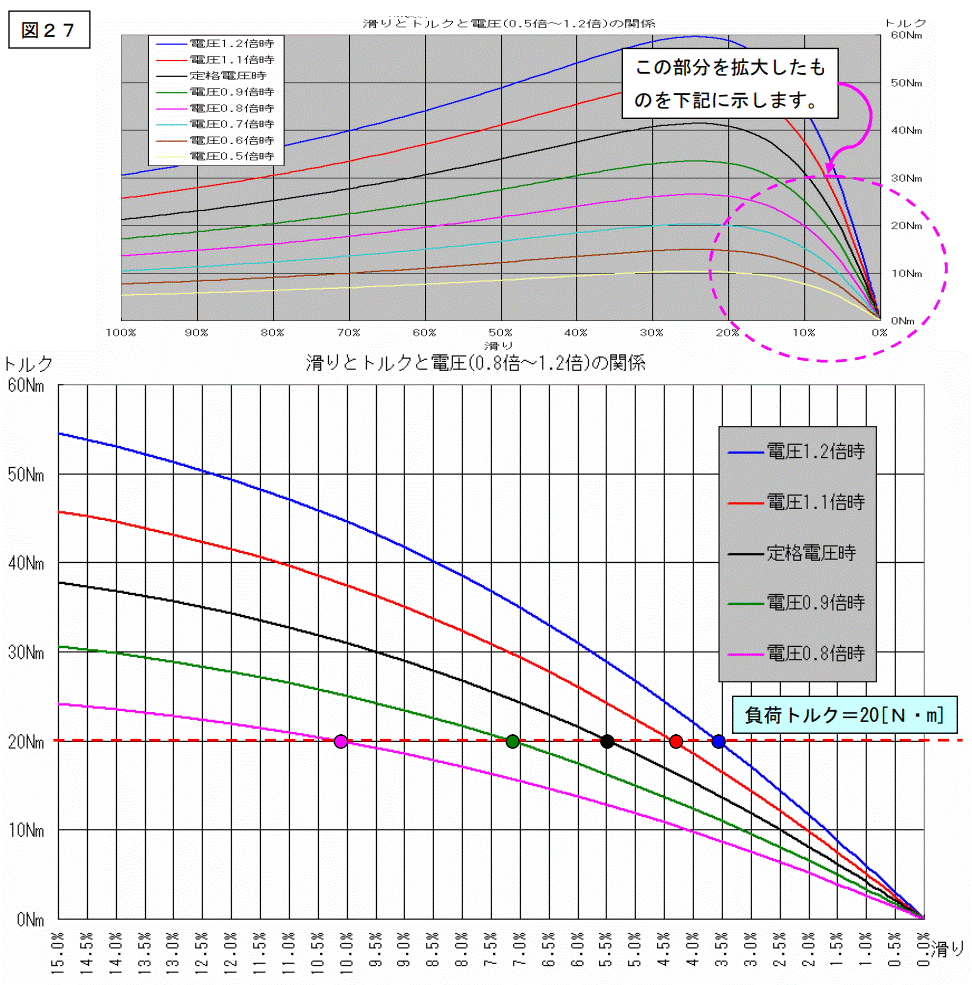
このグラフは、滑りが 0~15[%]の部分を拡大したものです。
滑り 15~100[%]の部分は使わない(使えない)回転領域ですから、解析から外します。
負荷トルクは 20[N・m]で一定とします。
電圧 0.5~0.7 倍時はグラフの範囲から外れる、又はトルクが最大でも 20[N・m]に満たない為、削除しました。
●●●●●が各々の電圧での動作点です。
この様に、負荷トルクが一定の場合、電圧を上げると滑りが減り、電圧を下げると滑りが増えます。
このグラフと、電流のグラフを比較します。
次ページ参照。
下図を見ると解りますが、各滑りに応じた電流は、滑りの増減と反対になります。
つまり滑りが増えれば、電流は電圧が下がったにも拘わらず増える事が解ります。
これらの関係を別のグラフで次ページに示します。
電圧の変化と、滑り、電流の変化を別にグラフ化したものです。
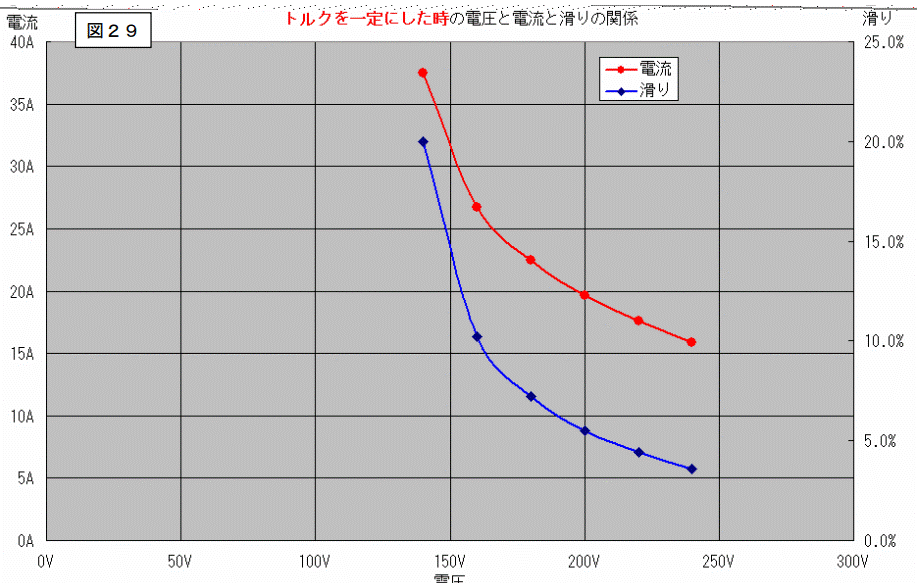
トルクが一定になるようにした場合、電圧が増えると電流及び滑りとも減少することがこのグラフからハッキリと読みとれます。
電圧が減った場合は逆です。電流及び滑りが増えます。増え具合、又は減り具合は、単純に反比例という事では無いようです。電流だけでなく、他の値の検討を行うと、定格電圧から電圧が90%に下がった場合で、軸出力、消費電力、効率、力率を各々を見ると次のようになります。
トルク=20[N・m]で一定とした場合です。
軸 出 力:5966[W]から 5857[W]に減少する。
消費電力:6661[W]から 6765[W]に増加する。
効 率:89.57[%]から 86.57[%]へ低下する。
力 率:97.89[%]から 96.58[%]へ悪化する。
この様に、電圧を上げたり下げたりすることに依る結果は、いわゆる電気の常識とはまるで異なる結果になりました。ところで、これまで散々検討してきた内容は、概ね軸出力が 5.5[kW]の 200V 級誘導電動機の場合の話です。
他の電動機はどうなっているのか? そもそもこれらを検討した時に設定した回路定数は現実の話として正しいのか? 等々疑問は次から次へと湧いてきます。苦肉の策で、懲りもせずに次の解析手法を考えます。
冒頭の苦肉の策をもう一度引っ張り出します。
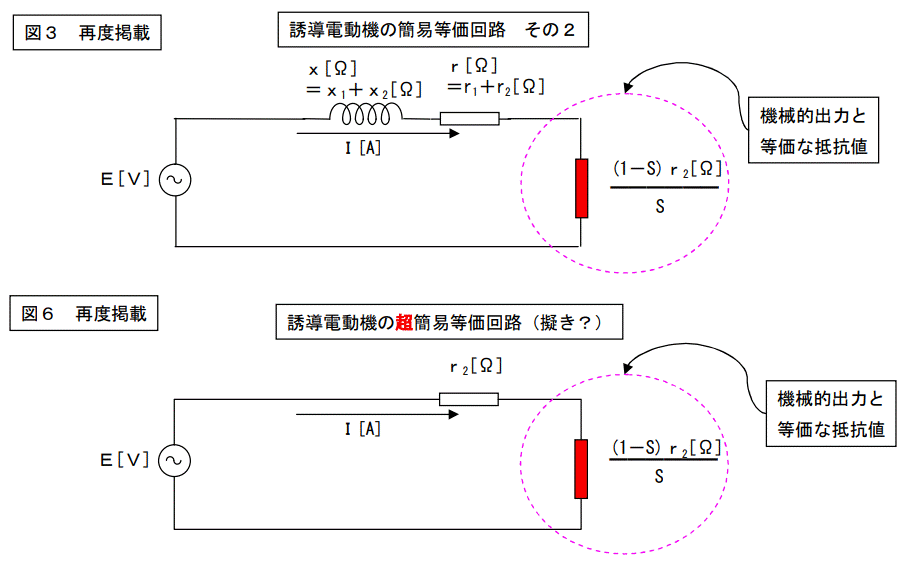
この2つの回路はどう考えても「ほぼ等しい。」とは言えません。
「全く違う回路だ。」と言えるかと思います。
因みに、電流と滑りの関係をグラフ化してみると下図のようになります。
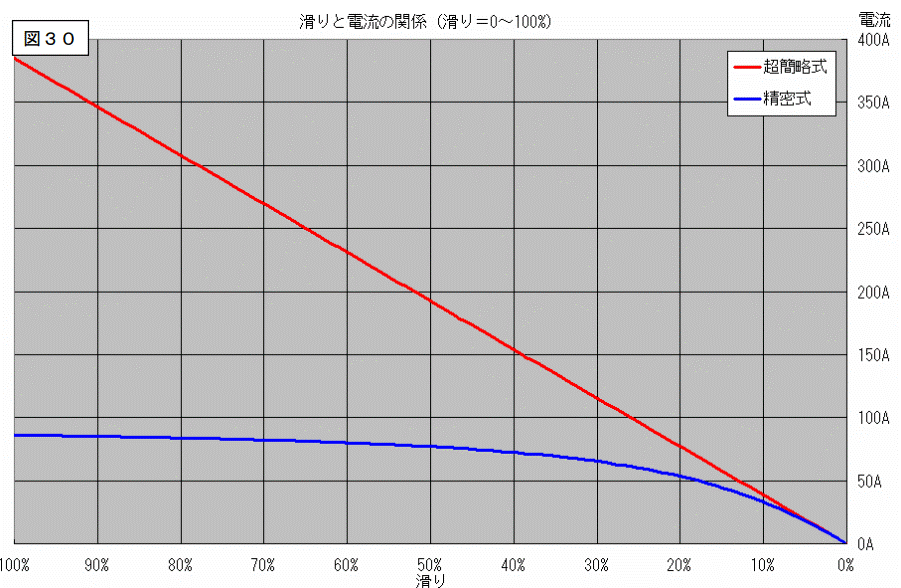
この様に全く違うグラフになります。
この様に、電流値のグラフは2つの回路で「違うグラフ」として描かれます。
このグラフ(図30)は、「滑り=0~100%」の範囲を描いたものです。
このグラフの滑りの範囲を変えて見ます。
誘導電動機は「滑り=数%」の範囲で使うのが不通です。
乱暴な言い方をすれば「滑り=10~100%の範囲はどうでも良い。」と言うことになります。
滑りの範囲を「滑り=0~10%の範囲。」に限ってグラフを描いてみると、見方が変わります。
下図参照。
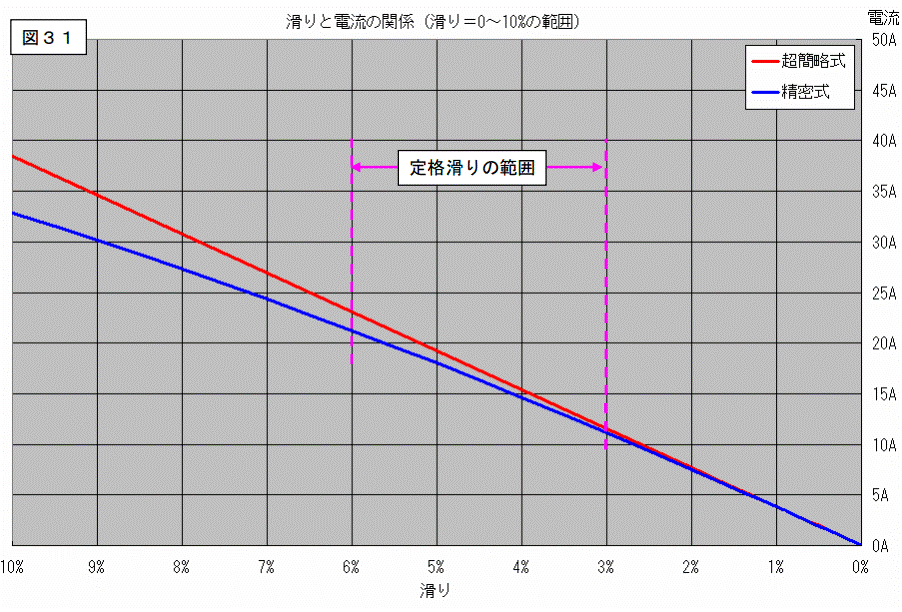
このグラフをどう見るかは、人それぞれだと思います。
誘導電動機の定格滑りは通常 3~6[%]程度です。
この範囲に限って話をすれば「多少の誤差は有るが、同じと見なしても実害は少ない。」と言えると思います。
USO800の話では無く、USO80位の話になると言うことです。次ページに他のグラフを掲載します。ヨーク見て下さい。
軸出力のグラフです。
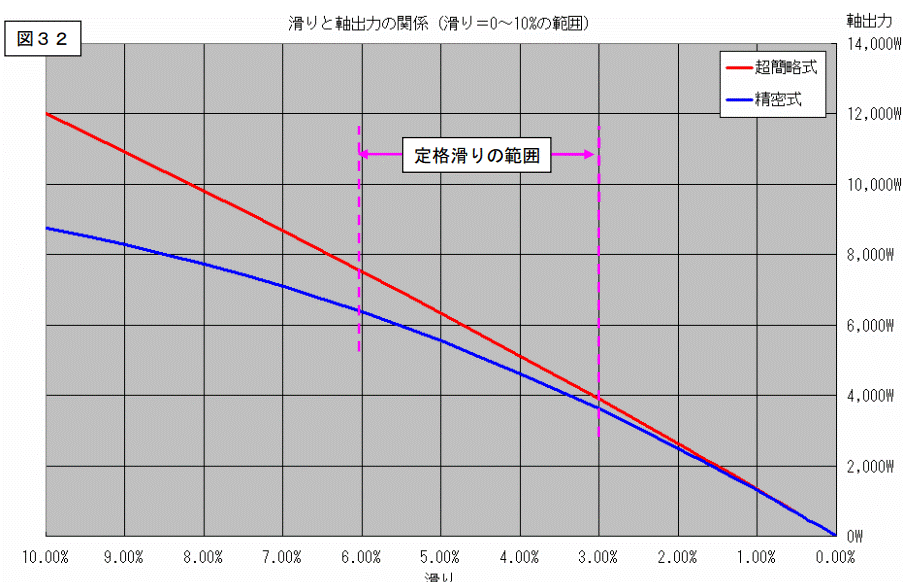
トルクのグラフです。

この様に、各値は通常の定格滑りの範囲内で有れば、2つの回路の値が大きく異なることは有りません。(相当に強引な結論です。)
冒頭に示した「超簡易等価回路(擬き?)」で解析した結果も、使おうと思えば使えます。
完全に荒唐無稽の話では有りません。従って、冒頭で計算した、等価回路擬きの計算は、滑りの範囲を限定すれば、何とか使える式になります。もう一度、等価回路擬きで計算した結果を示します。

精密式の計算式は下記です。
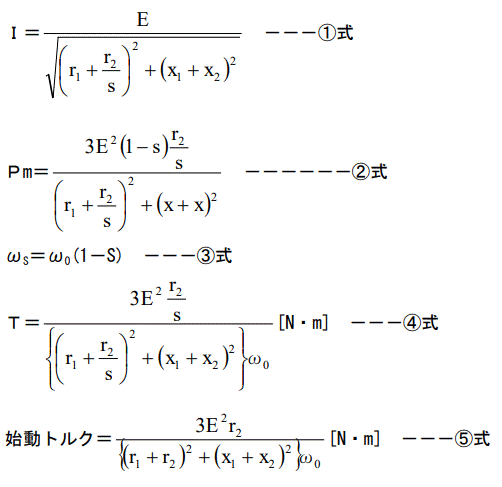
何方かこの数式を使って、一般式として電圧と電流が反比例することを証明して頂けないでしょうか。
小生の数学力では手に負えませんでした。
次ページに他の特性の事を少し書きます。
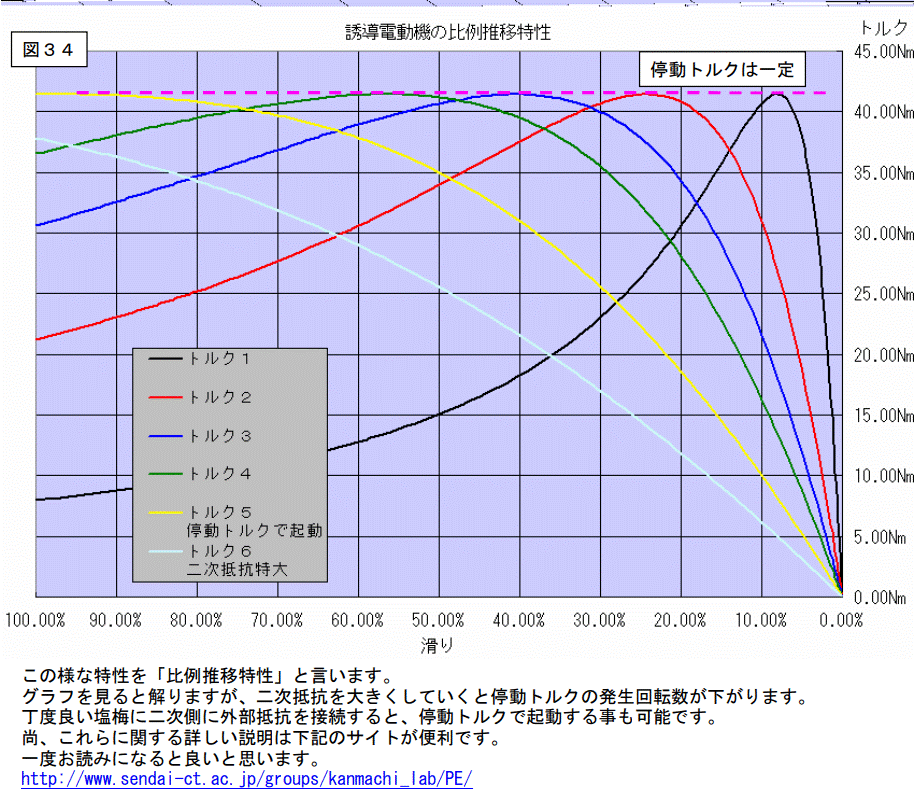
誘導電動機には、「停動トルク」が有ります。
定格運転時に、負荷トルクを増大させると誘導電動機は滑りを増やしてトルクを増大させ、これに対応します。負荷トルクをさらに大きくしていくと、いきなりストンと止まります。
これ以上のトルクには耐えられずに、動きを止めてしまうので「停動トルク」と言います。早い話、最大トルクです。このトルクの値を計算する式です。
トルクは精密式を使って下記のようになります。

となります。
⑦式と⑧式をヨーク見ると次のような事が解ります。
⑦式で、r1,x1,x2の値を固定値とすると(通常、これらの値は固定値。)滑り S は r2 の一次関数になる。これは、二次抵抗の値を変化させると、停動トルクの発生回転数を変化させる事が出来ることを示します。籠形の誘導電動機は二次抵抗の値を変化させる事は出来ませんが、巻線型の場合、外部抵抗を接続すると、二次抵抗の値は、色々と変化させる事が可能です。
又、⑧式では、r2 の値が出てきません。
これは、二次抵抗の値と停動トルクの値が無関係で有ることを示します。つまり、r2 の値を変化させても、停動トルクの値は変わらない事を意味します。
結果として下記のことが言えます。
停動トルクの値は電動機が固有に持つ値で、二次抵抗の値とは無関係。二次抵抗の値を制御すると、停動トルクの発生回転数を制御出来る。これらをグラフに示すと、次ページの様になります。
ところで、⑥式の微分方程式はどうやって解いたの?・・・・知るか!
参考書の丸写しだよ。文句が有るか!!
コホン、少し乱れました。次ページのグラフをご覧下さい。
オシマイ

コメント