ここでは、四端子定数について説明します。
四端子定数?
ナンジャソラ?
な状態でしたが、なんとなく理解できたのでまとめてみました。
四端子定数の概念
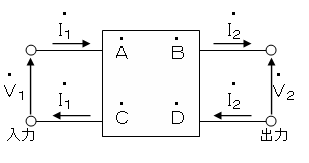
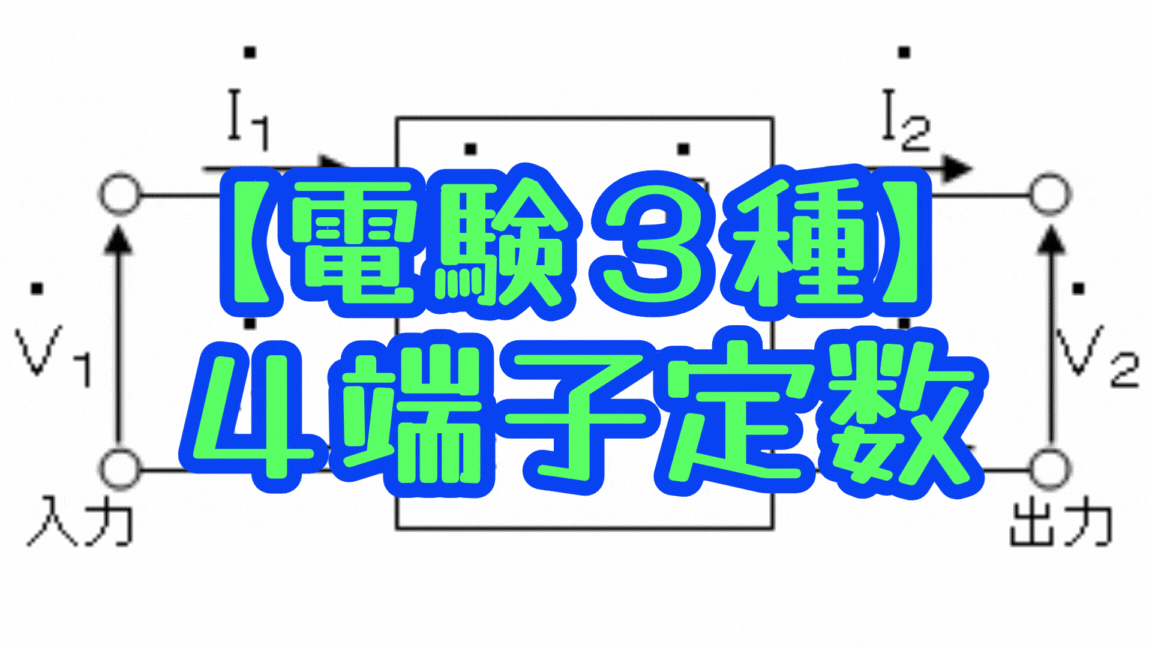
図のような回路に於いて、、、
・入力電圧をV1、入力電流をI1
・出力電圧をV2、入力電流をI2
とした時に、、、(ここまでは意味が分かる)
V1=AV2+BI2
I1=CV2+DI2
と表現した時の
A,B,C,Dを四端子定数という。
ハァ?意味がわからん
という状態に陥って、なんとなく読む気がなくなります。
こ、ここは百歩譲って、上のような式で表せるんだ!ということで話を進めてください
ここで四端子定数のコトを述べます、、、
回路の四端子定数というのは、予め4つの定数を求めておくことで入力と出力の電圧・電流の関係を調べるときに、回路のこまごました計算をする必要がなくなり便利なものである。
ふむ、、なんとなく便利そう。
ということで平たく言えば、右上の図でいう「A,B,C,D」と書かれてある部分が回路です。
この中はどうなっていてもかまいません。
最初に回路を組み立てた時だけ”四端子定数”を求めておけば、後は回路の中を気にしなくても計算できる!
というものみたいなんです。
便利そうです。
では、実際の四端子定数はどうやって求めるんでしょうか?
これは、出力端子を開放した時と短絡した時を考えて算出します。
具体的には、
という大前提を元に考えていきます。
この2つの前提条件を、最初に出てきた2式に当てはめます。
V1=AV2+BI2
I1=CV2+DI2
これだけのコトです。
それでは次に示す実戦問題で簡単な回路で四端子定数を求めてみましょう。
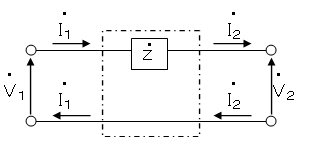
回路に「Z」というインピーダンスが1つだけある回路で考えます。
この回路の出力端子を開放したり短絡したりすることで各定数を求めていきます。
出力を開放した計算
では
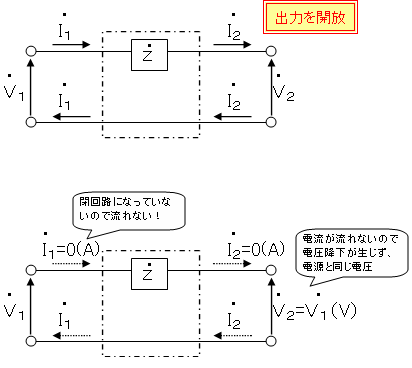
まず最初に出力を開放した場合
を考えてみます。
この場合、出力が開放ですので、
出力電流が流れませんのでI2が”0”です。
電流が流れないので電圧降下が生じず
V1=V2となります。
・I2=0
・V1=V2
この2式を当てはめてみましょう。
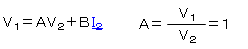
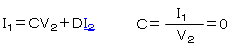
これで、『A』『C』が求まりました。
出力を短絡した計算
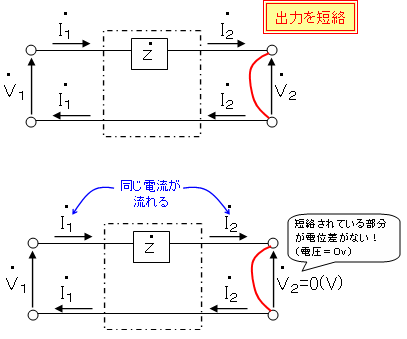
では次に、 出力を短絡した場合
を考えてみます。
この場合、出力が開放ですので、
出力電流は入力電流と同じものが流れるのでI2=I1となります。
電流が流れることで電圧降下が生じ
V1=Z×I1となります。
・I2=I1
・V1=Z×I1
この2式を当てはめてみましょう。
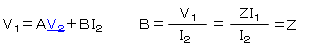
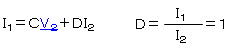
これで、『B』『D』が求まりました。
まとめ
この解き方は超基本ですが、考え方(解き方)はどんな回路に於いても変わりません。
この四端子定数は、送電系統やトランジスタ回路にも使われています。応用範囲は広くあります。
電験では、3種のみならず1種・2種において四端子定数を求めよという問題も出題されます。 この”超基本”をおさえておけば応用してゆくことができます。
コメント