同期発電機の運転いろいろ
同期発電機の運転方法は色々あります。一般的な教科書や参考書では電力会社の発電機の話が多いようですが、自家用で買電とパラランした時の事象を書いたものを見たことがありません。そこで作ることにしました。毎度ながら独断と偏見だけで書いてますし読んでも参考にならないかも知れませんがお付き合い下さい。

平成 鹿年 骨月 吉日
サイタマドズニーランド大学SDU学長 鹿の骨記
解析の前提として同期発電機の同期インピーダンスは同期リアクタンスのみとします。図0参照。
実機に於いて、同期抵抗<<同期リアクタンスの関係にありますのでこの条件でも大きく間違った結果にはなりません。これからベクトル図を書いて色々考えてみましょう。
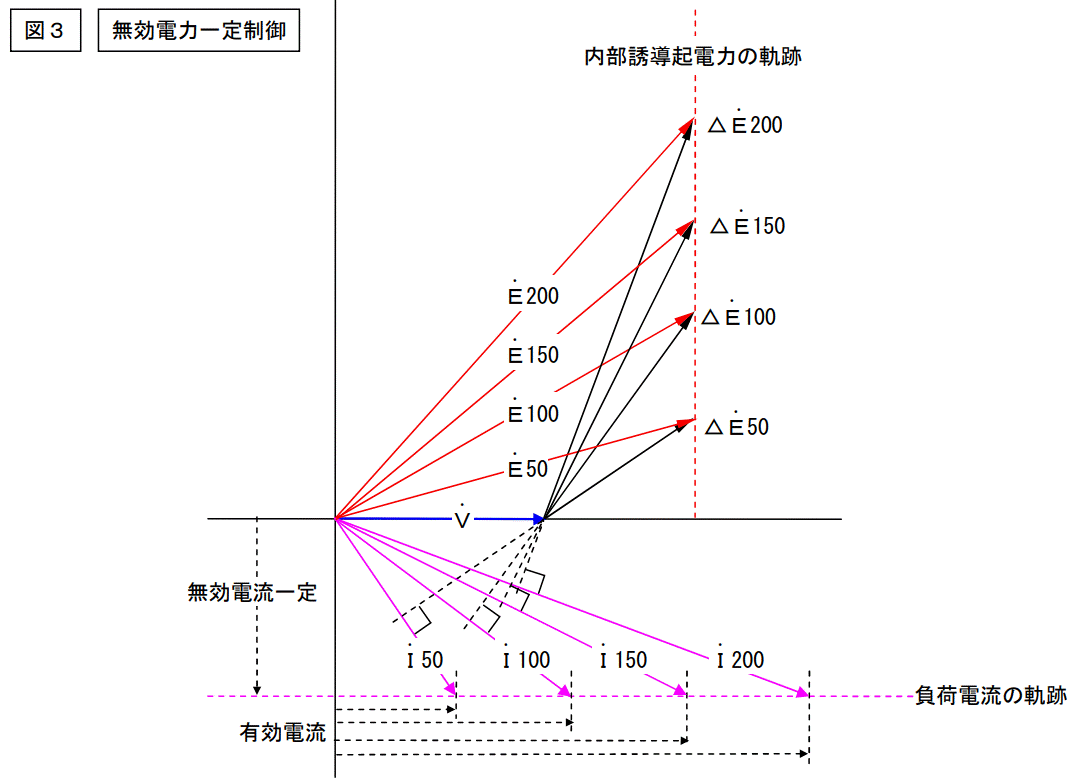
取り敢えず2つのベクトル図を書いてみました。

何やら怪しげなベクトル図です。
図1の状態を取り敢えず最初の状態として出力を1.5倍にしたのが図2です。図をよく見ると解りますが、端子電圧Vは一定です。これは発電機が短絡以外の何をしても電圧が変わらない事を意味します。受電点の電圧は系統の都合により勝手に決まります。自家用側の発電機が何をしようとおいそれと変わるものでは無いのです。(本当は少し変化する。)
また無効電流が一定になっています。これは「そうなる。」のでは無く「そうしている。」からそうなります。端子電圧と無効電流をかけ算すると無効電力が求まりますが、図に示すような制御の手法を
「無効電力=一定制御」
と言います。
何故このような手法を取るのか後で説明します。
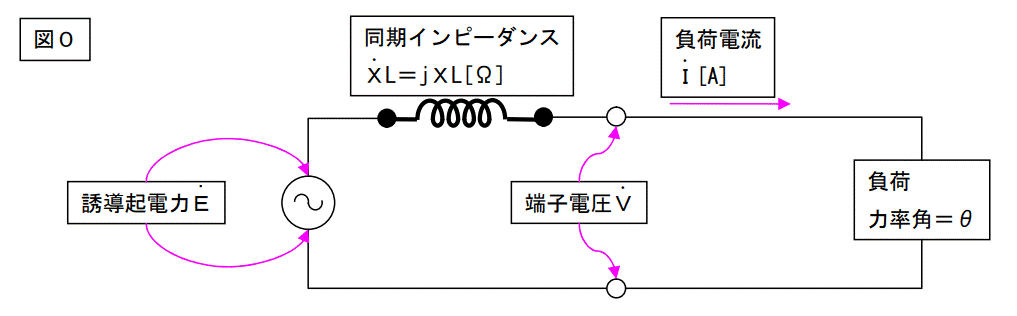
負荷を 50~200%で変化させた場合のベクトル図を重ねると図3になります。何がどの様にどう変化するのかをよく見て下さい。特に内部誘導起電力の軌跡に注意して下さい。
内部誘導機電力を図4の様に横一列に並べて見ると解るのですが、出力に応じて励磁電流の値は異なり内部誘導機電力も変化します。

言い換えれば無効電力一定制御の場合、出力に応じて励磁電流の値は決まっていると言うことです。また、この図には現れていませんが、出力に比例して機械的原動機の出力は変化します。出力を増やすには機械的な入力が増えないと辻褄が合いませんし、減る場合も同様です。
このように設定した出力になるように運転する事をLL運転と言います。
LL:Limited Load です。
この時の周波数は買電に依存します。
例えば買電が 50.1Hz になれば発電機も 50.1Hz になり、買電が 49.9Hz になれば発電機も 49.9Hz になります。発電機で周波数維持に責任を持ちません。
今度は励磁電流が一定で出力を変化させたら何がどうなるのかを次項に書きます。
励磁電流=一定と言うことは内部誘導起電力が一定と言うことになります。これで機械的入力を増減させたら何がどうなってしまうのでしょうか。
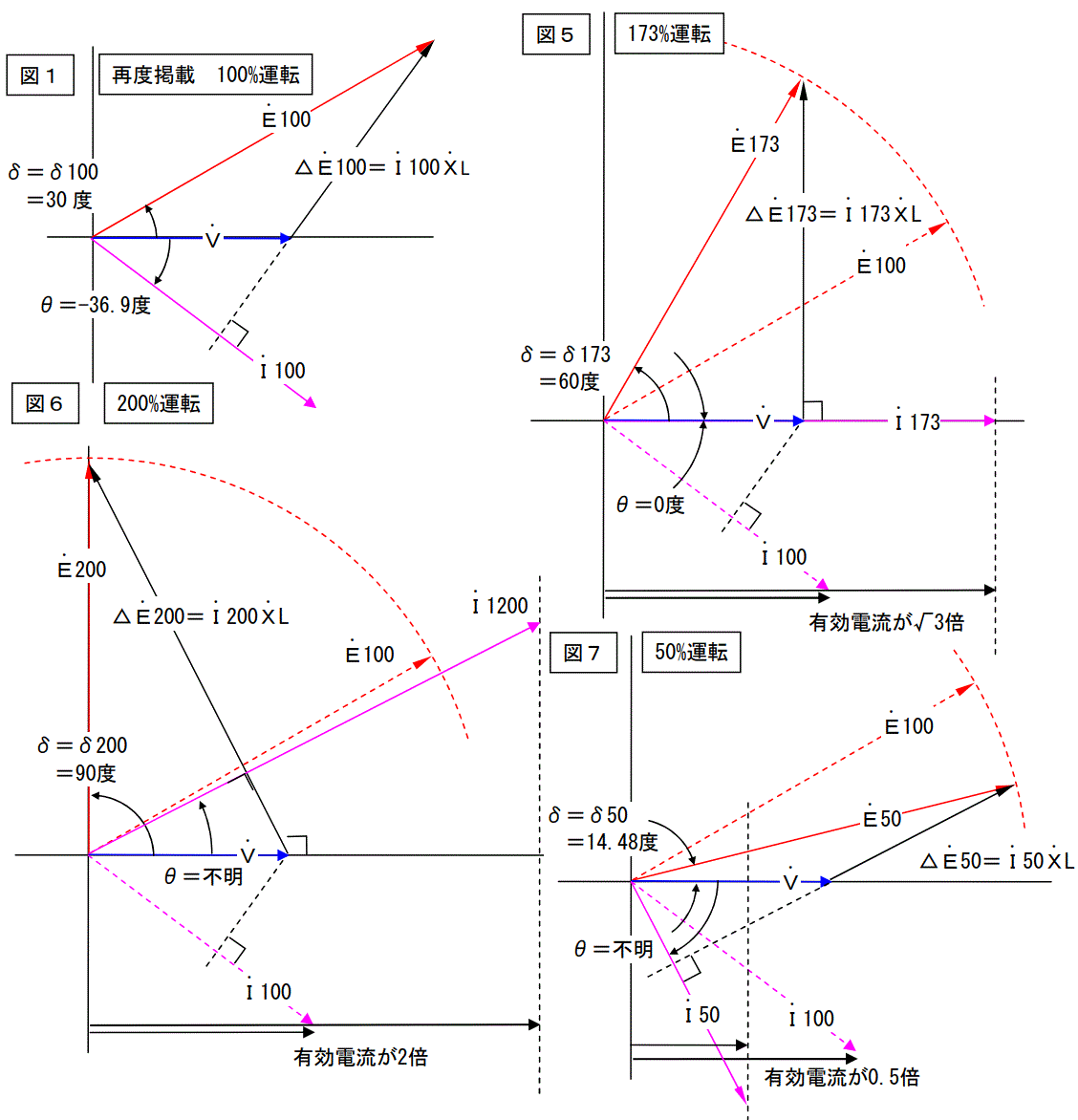
図5が√3倍、図6が2倍の場合、図7が0.5倍の場合を書いています。出力端子電圧及び内部誘導起電力は変えていませんので出力は負荷角δのsin値に比例します。
(P=EVsinδ/Xの公式に当てはめる。E,V,Xを一定にすると出力の変化はsinδに比例。)
従って√3倍の場合の負荷角δ173は60度になり2倍の場合は90度になります。この時の電流値及び力率角θは不明ですが、有効電流の倍率が√3倍及び2倍になることが解っていますので幾何学的に求めて作図をしています。
従って図6の場合の力率角θは計算できていません。図7も同様です。図5~7を見ると解りますが、このような制御を行うと負荷角δ及び力率角θが大きく変化し現実的ではありません。
図3と比較すると解りますが出力が2倍の場合図3は安定的に運転できますが、図6は安定の限界でこれ以上出力を増やすと負荷角δが90度を超え同期外れを起こします。
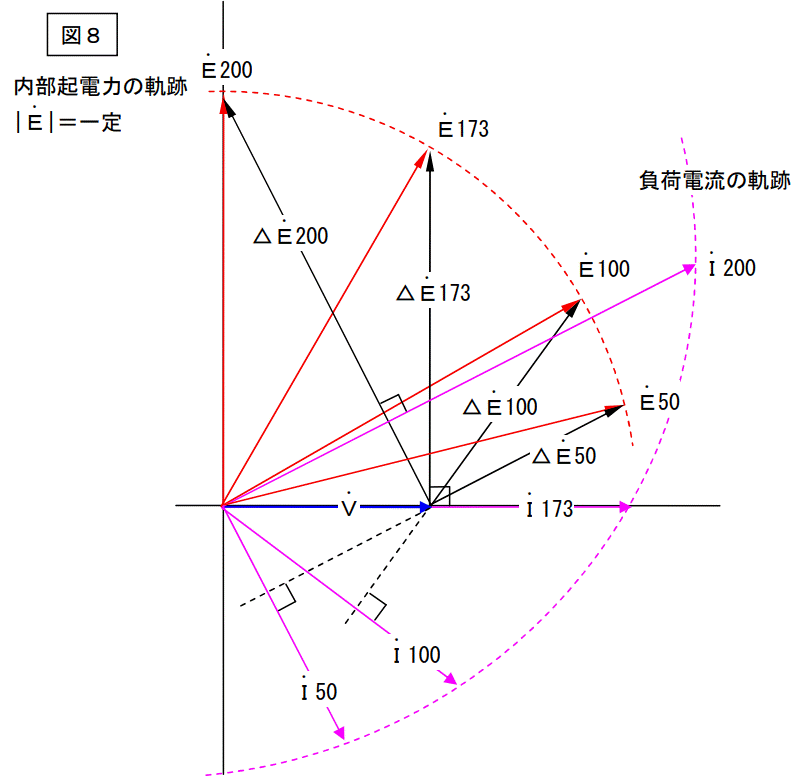
また図には示していませんが、無効電力(=無効電流)の値が勝手に変わるのも理解して下さい。次ページにこのベクトル図を重ねたものを記載します。
良く解らない重ね図が書けました。内部誘導機電力は励磁電流=一定ですから絶対値が変わりません。従って内部誘導起電力の軌跡は半円になります。負荷電流は軌跡を辿ってみると半円に成りそうですが軌跡の式は見つかりませんでした。
次は機械的な入力を一定にして励磁電流だけを増減させた場合の解析です。次ページに示します。
機械的な入力を一定にして励磁電流だけを増減させた場合の解析です。
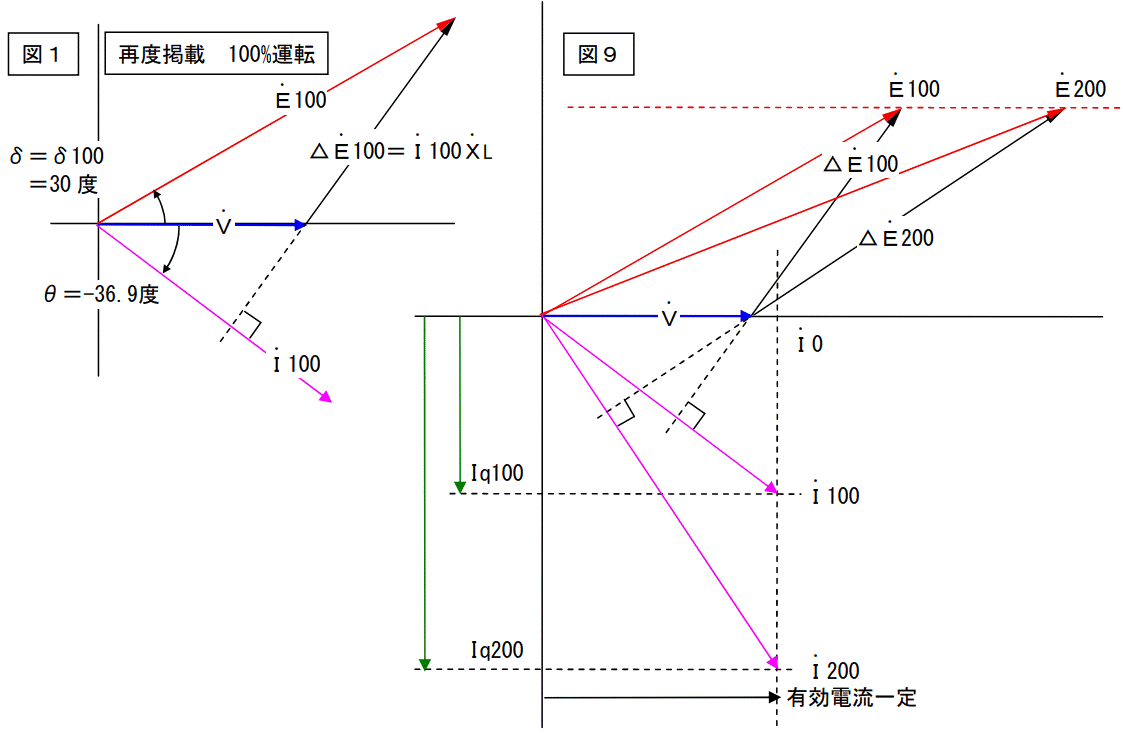
図1は元の状態で図9は無効電流が2倍になった場合を書いています。無効電流が2倍~-1倍に変化する図を重ねると図10になります。励磁電流だけを操作すると無効電流が変化することが解ります。つまり励磁電流の制御を行うと無効電力の制御が出来ることになります。

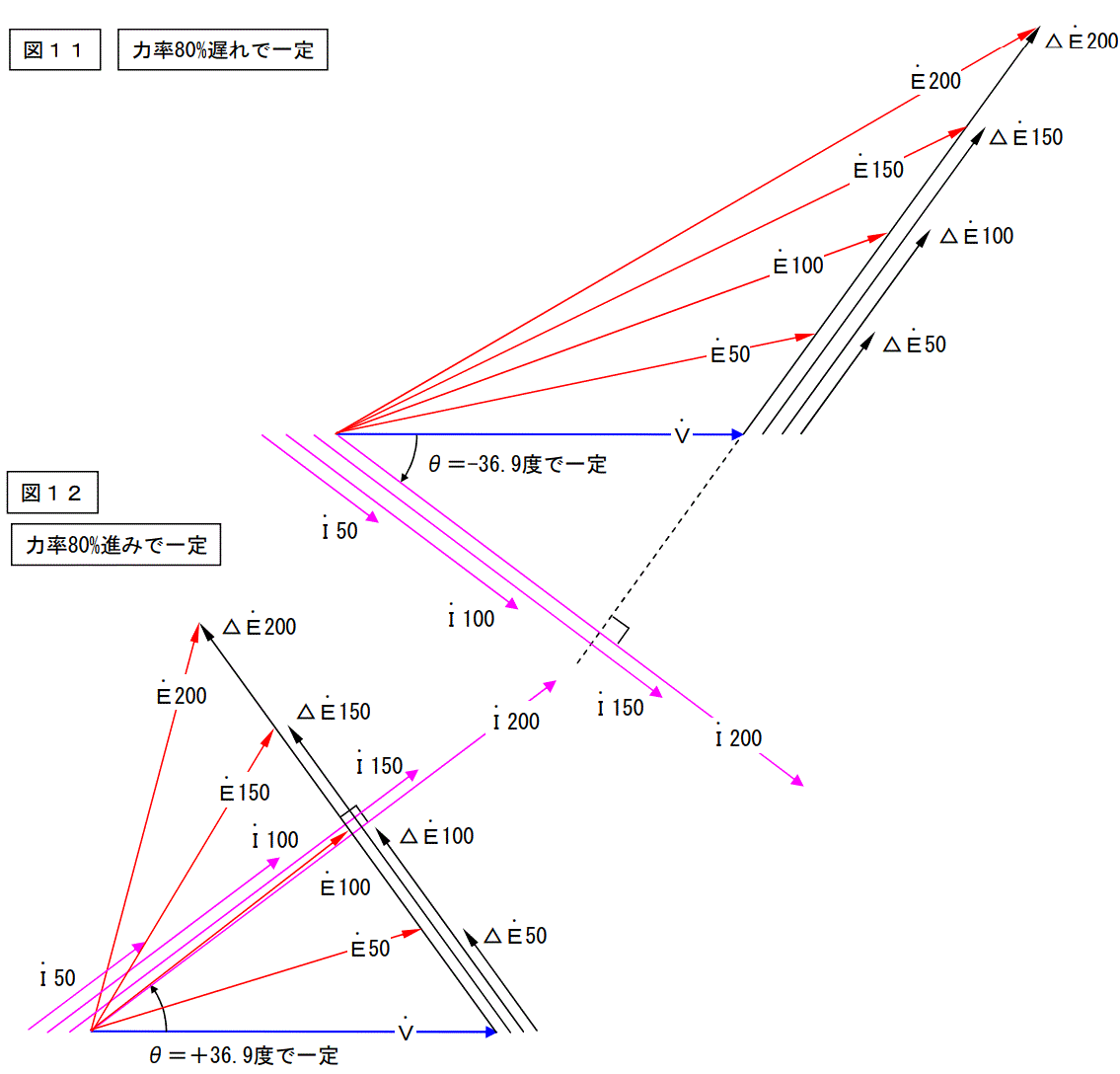
余りやらないと思うのですが力率が一定の場合の解析です。(作図の都合上少し値を変えています。)
取り敢えず此処まで
コメント