CT(変流器)は実務上よく扱うものです。配線変更やCT回路の作業において、1次側に電流が流れている時にCTの2次側回路を開放(オープン)には絶対にしてはいけないと先輩に言われると思います。一般的には「非常に高電圧が出て危険」という話ですが、このことについて理論上の説明となります。
CTの二次側を開放しては何故イケナイのかという話【第1部】
さて今回のお題は「CT」に関するものです。
配電の実務ではCTを沢山使います。
CTは大電流を計測するのに必要な機器ですが、二次側を開放したまま一次側に電流を流すと、とんでもない事になります。
何故こんな事になるのかと言う話です。
この話は電気技術者として確実に理解しておかなければならない事項です。
下記の説明(擬き?)をお読み下さい。

平成 鹿年 骨月 吉日
貧電工附属 サイタマ・ドズニーランド・大学 学長 鹿の骨
で・・・、毎度の様にいきなり問題を出します。
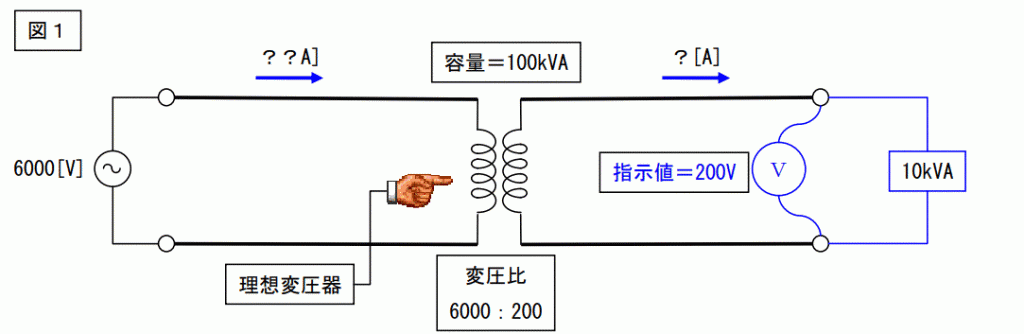
問題1
図1に示された回路の、?及び??の電流値は幾つか?
問題2
変圧器の巻数比は幾つか?二次側を「1」として答えよ。
解答
暗算で求まる問題です。
問題1
?[A]=10000[VA]÷200[V]=50[A]
??[A]=10000[VA]÷6000[V]≒1.67A]
問題2
一次側:二次側=6000:200=30:1
幾ら何でもこれが解らないとは言わないで下さい。
変圧器の回路定数は全て無視しています。変圧器の容量は計算と無関係です。
引き続き次の問題を解いて下さい。
問題3
一次側と二次側の変圧比は幾つか?二次側を「1」として答えよ。
問題4
一次側の電流と二次側の電流の比率は幾つか?一次側を「1」として答えよ。
解答
これも暗算で求まります。
問題3
一次側電圧:二次側電圧=30:1
問題4
一次側電流:二次側電流=1:30
此処までは当たり前の話です。
問題4の答えを覚えておいて下さい。 <==結構重要です。
さて今度も問題を出します。
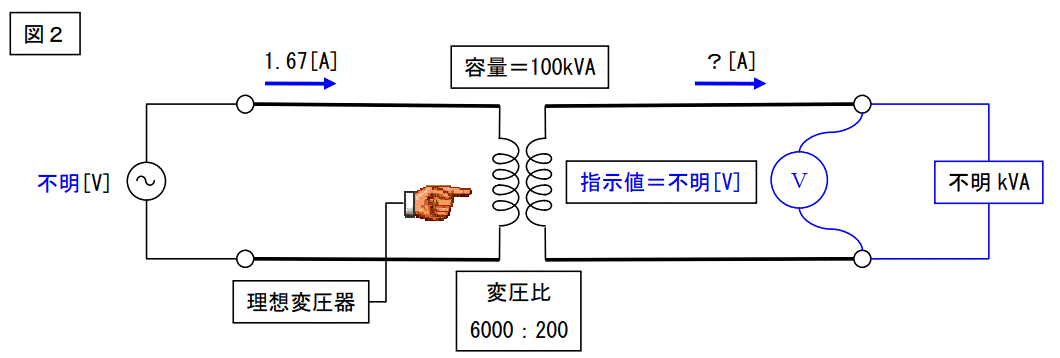
問題5
図2に示された回路の一次側の電流が 1.67[A]であった。
一次電圧、二次電圧は不明で、二次側に接続された負荷容量も不明である。
この時の二次側電流、?の電流値は幾つか。
解答
変圧比は 30:1 である。
つまり二次側の電流は一次側の電流の 30 倍となるので、?電流=1.67[A]×30 倍=50[A]となる。
解説
此処で注意したい事は、変圧器は変流器にもなっている事です。
前ページの問題1及び問題4をもう一度見て欲しいのですが、問題1で計算した結果とこの問題5は同じ結果になっています。
じゃあ・・・この時の電流は、電圧が問題1と同じ一次側 6600V、二次側 6600V、二次側 200V の時だけ成立するのか? 200V の時だけ成立するのか?と言う事を考えて下さい。
解説は旨く出来ませんが、この時の電圧は一次側が 6600V になっている必然性は全くありません。
幾つでも良いのです。
ここで理解して欲しい事は下記です。
一次側二次側の電圧に関係なく一次側電流対二次側電流の比率は変圧比の逆数になる。
つまり下記の式になります。
一次電流:二次電流=1/変圧比:1=1:変圧比(変圧比は二次側を1としている。)
くどいようですが、これは非常に重要な事です。
変圧器は文字通り電圧を変換する機器ですが、この様に電流を変換する機器=変流器にもなっています。
一次側に流れた電流の変圧比倍の電流が必ず二次側に流れる事を理解して下さい。
一次側に電流が流れて二次側には流れないという事は絶対にありません。
(理想変圧器で考えた場合に限る、実際は励磁電流が単独で一次側には流れる。)
さて次ページではCTの原理に迫ります。
下図はCTを単相の回路に接続した場合を描いています。
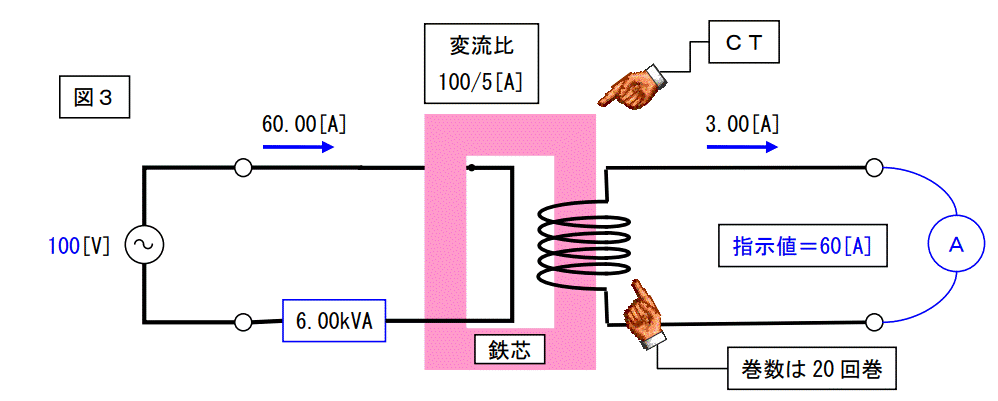
ここで問題
CTの二次側の巻数は20回巻である。では一次側は何回巻き?
怪盗
二次側回路は「20 回巻」と言っているから確かに20回巻いているのだと思う。
しかし、一次側は鉄コアの真ん中を一次導体が貫通しているだけで、巻いてはいないのでは無いのか?
実は・・・一回巻になっています。下図参照。
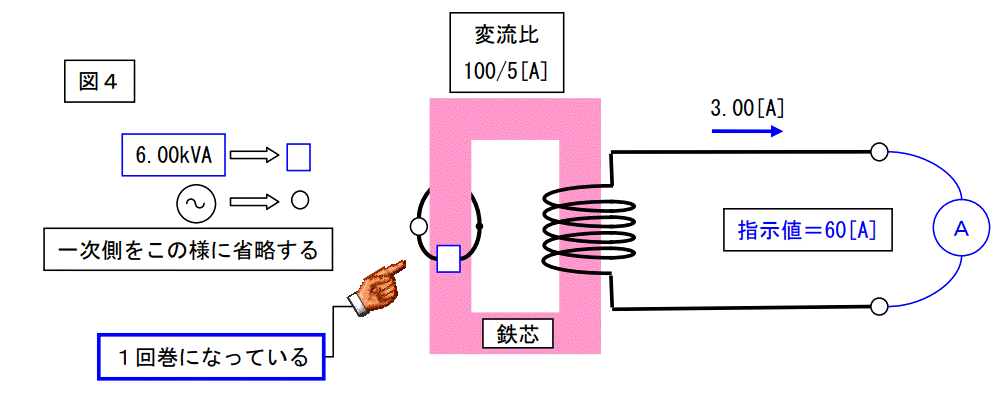
一次側が1回巻になっている事をご理解願えたでしょうか?
この図4をヨーク見ると、次の事が解ります。
コレって、変圧器ジャン!
その通り!
でも何となく普通と違うのです。
何処がどう違うかを次ページで考えます。
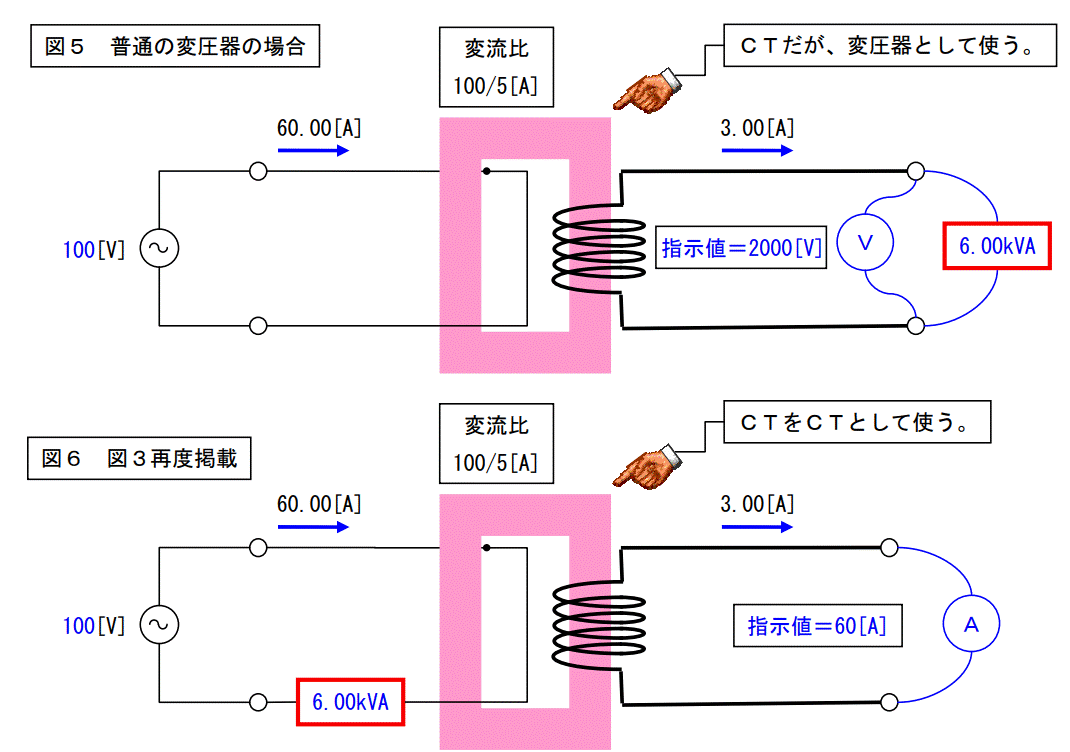
図5の場合と図6の場合、何処が同じで何処が違うのかを見ます。
同じ所
一次側は1回巻、二次側は20回巻の変圧器になっている。
だから、一次の電流:二次の電流=20:1に必ずなる。
違う所
負荷の位置が違う。
図5の場合は負荷が二次側に接続されている。
これは変圧器の使い方としては普通の使い方である。
因みに二次側の電圧は一次側の20倍になるので2000Vになる。
二次電流は6000VA÷2000V=3.00Aとなる。
一方図6では負荷が一次側に接続されている。
図5とは全く違う。
この時、図6で一次側に流れる電流は、CTがある場合と無い場合で違う電流になるか?
ならない!!
つまり、CTから見ると、一次側の電流は「定電流電源から供給される電流」に見えます。
CTの都合で一次電流は決まりません。
図5の場合と決定的に違うところです。
では図6で、この時の一次電圧は何Vか?
定義されない! 早い話、ワカンナイ!!
では、二次電流はどうなるか?
一次電流の20分の1に、必ずなる。 <==最重要項目!!
一次側の電流の1/20の電流が必ず流れます。
変圧器は変流器にもなっています。
従って、変圧比が1:20の変圧器の電流比は20:1に必ずなります。
これを図示すると次ページの様になります。
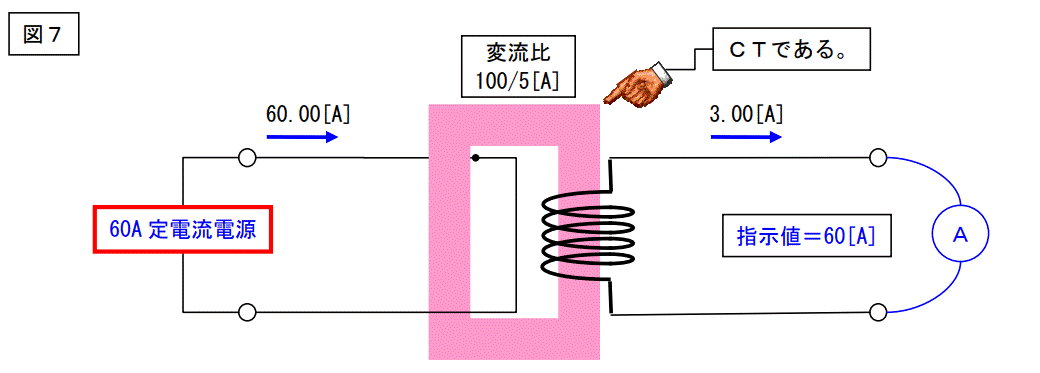
上図に示すように、一次側に「定電流電源」を接続した場合と等価になります。
通常の場合、電源と言えば「定電圧電源」ですが、今回の場合は「定電流電源」です。
ここで問題
二次側に下記のような抵抗器を接続した。
二次側に流れる電流I21、I22 及びI23 は幾つか?
電圧計の値は幾つを指すか?
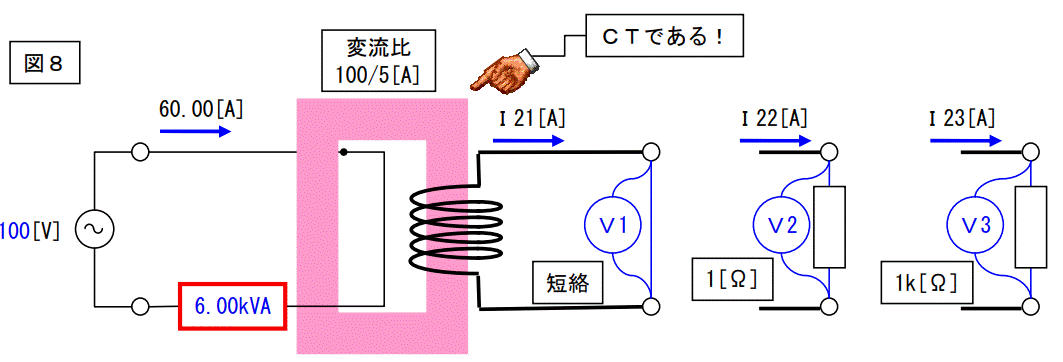
解答
二次側に流れる電流I21=I22=I23=3.00[A]で、全部同じです。
一次側の電流が 60[A]で固定されています。
従って、二次側の電流も 3[A]で固定されます。
何が何でも一次側の電流は 60[A]ですし、二次側の電流は 3[A]です。
電圧計の振れは、電流×インピーダンスで計算されます。
V1=3[A]×0[Ω]=0[V]
V2=3[A]×1[Ω]=3[V]
V3=3[A]×1000[Ω]=3000[V]
恐らく 1kΩの抵抗を接続した場合は、実現不可能だと思います。
二次側の端子電圧が 3000[V]にもなりますので、CTが壊れます。
もうお気づきだと思いますが、二次側の抵抗値が大きくなると、二次端子電圧は高い値になります。
ですから、端子を開放にして、∞[Ω]にしてしまうと、とてつもない電圧が発生します にしてしまうと、とてつもない電圧が発生します。
これで、取り敢えず説明は終わりです。
ものの本に依ると、二次側を開放すると「磁気飽和」が起きて二次側に高い電圧が発生すると説明されます。
これで、理解できる知識のある方は、この説明など読む必要は無いと思います。
小生を含め、通常ではこの説明ではチンプンカンプンでサッパリだと思います。
ですから、この様な解説書擬きを作ったわけです。
さて、次ページにオマケがあります。
図7に示す場合、一次電圧はどうなっているのでしょうか?
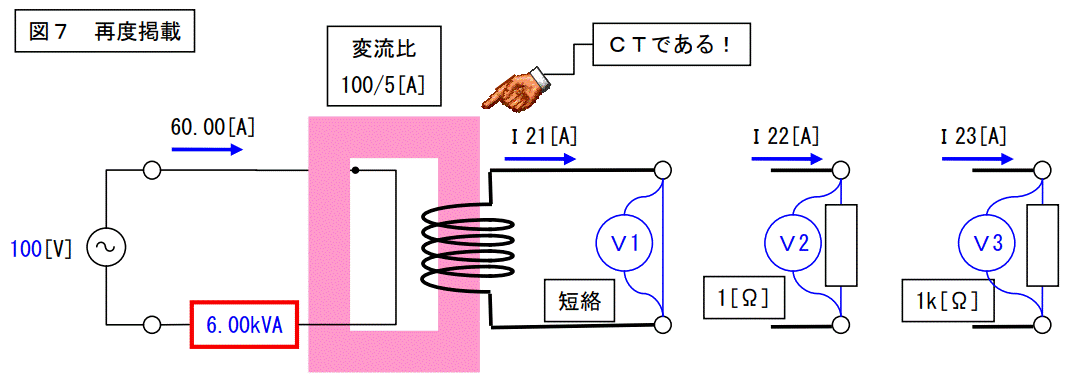
CTは「一次巻線が1回巻の変圧器だ。」と書きました。
これは間違っていない事項だと思いますが、上図の場合、変圧器の原則に従い、一次側には二次側の電圧の変圧比分の1の電圧が出ていなければイケナイ事になります。
例えば、二次抵抗がゼロ(二次回路は短絡)の場合、二次電圧はゼロ[V]ですから一次電圧もゼロ[V]で良いと思います。ところが、二次抵抗が1[Ω]や1k[Ω]の場合、一次電圧は各々、0.15[V]、150[V]になるハズです。
この電圧は何処に出ているのでしょうか?
ワカンナイです。ハイ!
これに関して、理屈を付けられないでいます。
何方か教えて下さい。
最終的に解って欲しい事は下記
変流器は変圧器と原理的には同じ。
一次側の電流と二次側の電流には変流比倍の関係がある。
二次電流=一次電流の変流比倍となる。(変圧器は変流器にもなっているのでこうなる。)
一次側に電流が流れれば、二次側にも電流が流れないと辻褄が合わない。
二次側を開放してしまうと、二次側に無理矢理電流を流そうとしてとてつもない電圧が発生する。
だから、CTの二次側は絶対に開放してはイケナイ!
オシマイ
CTの二次側を開放しては何故イケナイのかという話【第2部】
さて今回もお題は「CT」に関するものです。
前回のお話は最後の方が「?」で終わっています。今回はその続きです。
で・・・、前回は下記のような記載で説明が終わっています。
例えば、二次抵抗がゼロ(二次回路は短絡)の場合、二次電圧はゼロ[V]ですから一次電圧もゼロ[V]で良いと思います。
ところが、二次抵抗が1[Ω]や1k[Ω]の場合、一次電圧は各々、0.15[V]、150[V]になるハズです。
この電圧は何処に出ているのでしょうか?
ワカンナイです。ハイ!
これに関して、理屈を付けられないでいます。
何方か教えて下さい。
今回はこれを何とかしようという話です。早速ですが下図をご覧下さい。
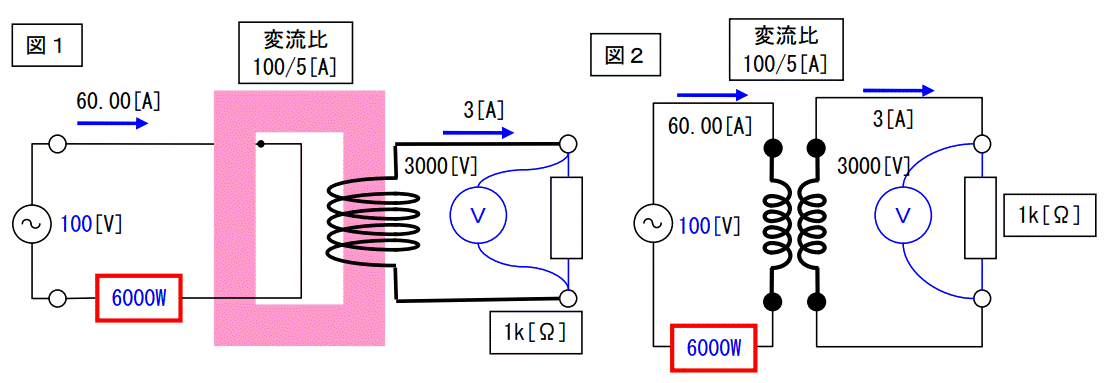
この二つの図は同じものを書いています。
図1は現物に近いものを書いていますが、概念的に理解しにくい所がありますので図2の様に書きました。
CTは図2に示すように変圧器を負荷と直列に繋いだ回路と等価になります。
この時に巻数比(=変流比の逆数)が 1:20 になっているだけです。
更に次のような事も考えます。
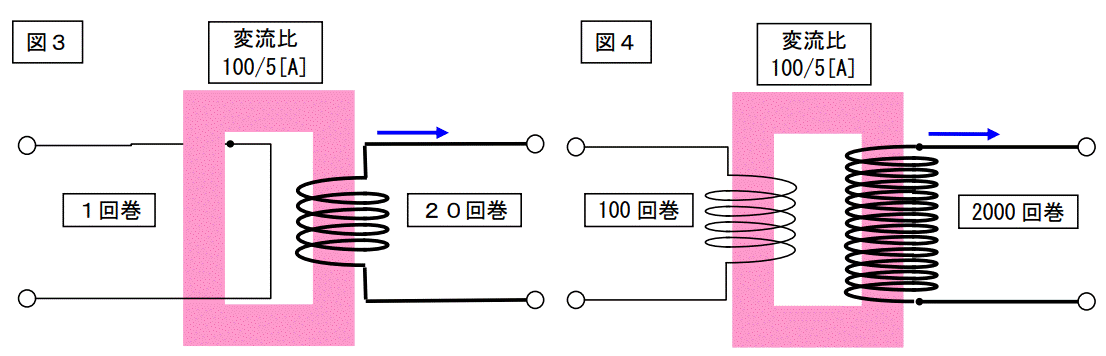
今回はこの二つの変成器は同じものとして扱います。
つまり変流器ですから変流比さえ同じだったら何回巻いてあっても結果は同じとします。
何なら一万回巻:二十万回巻でも良い訳です。
今回は図2の回路で図4を適用したものとして書いていきます。
さて此処で変流器のインピーダンス変換を考えます。
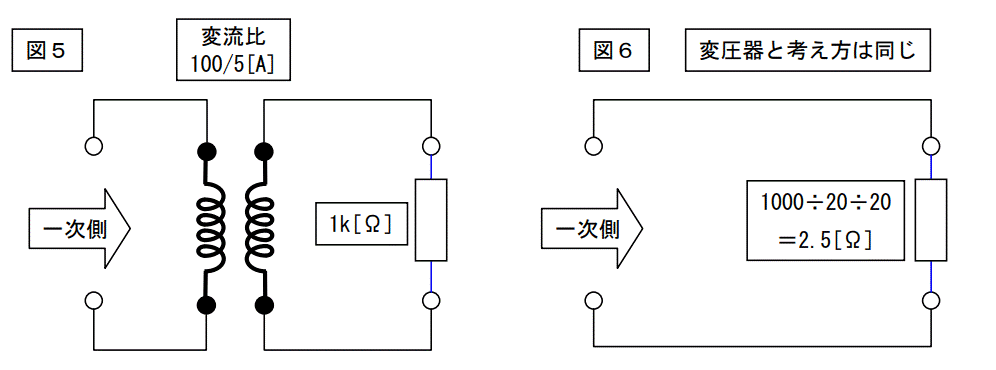
図5は二次側に 1kΩの抵抗負荷が接続されていますが、これを一次側に変換すると図6になります。
従って、前ページの図2は下記のように書けます。
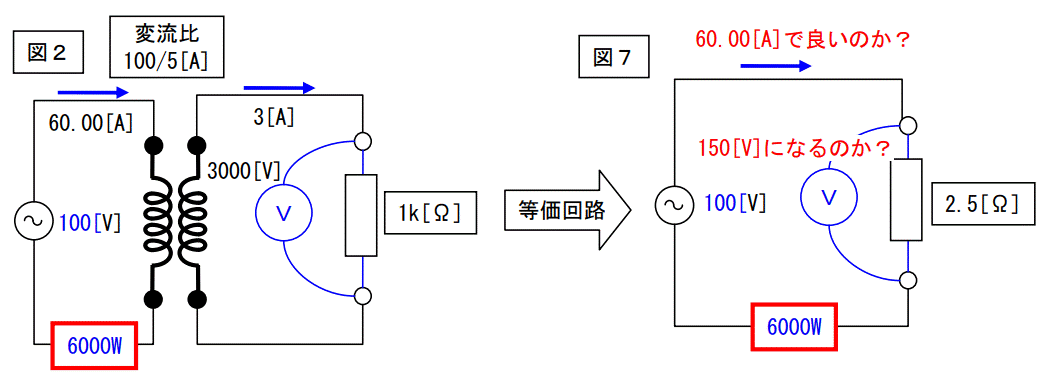
この時点で気が付く訳です。・・・図2は何処かおかしい、変だ!
この図7の回路で 60[A]流れるのか?と言う疑問がわきます。
前回は、此処で 60A]流れる、として考えましたがどうやらこの部分に理論の不足がありそうです。
図7をもう少し変形します。
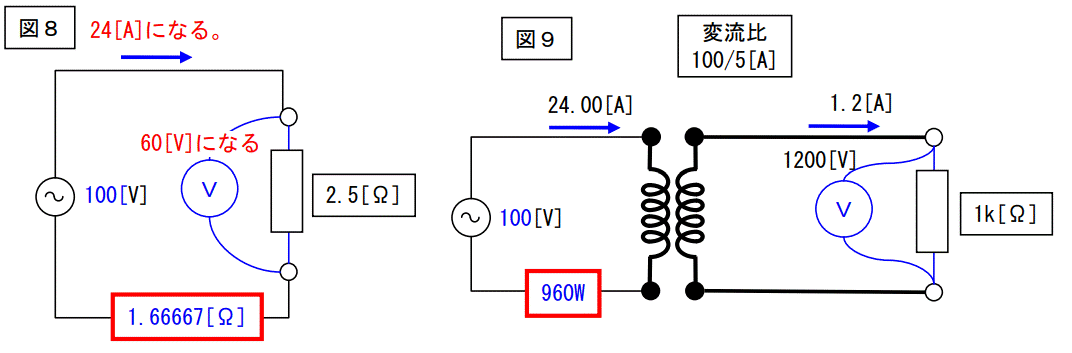
図7の6000Wの部分をΩ値に換算すると1.6667Ωになります。
従ってこの回路は電圧が100Vで抵抗が2.5+1.66667=4.1667Ωの回路になりますので電流は60Aでは無くて
電流=100V÷4.1667Ω=24A
となります。
自動的にこの電圧計の値は24A×2.5Ω=60Vとなり、この値で図2をもう一度書くと図9になりCT二次側の電圧は60V×20=1200Vとなり、二次電流は1.2Aとなります。
勿論実務ではこの様な事にはなりませんが、ならない理由は磁気回路に磁気飽和があるからです。
磁気飽和の話は少し横へ置いて、このまま磁気飽和が無いものとして話を進めます。
1k[Ω]の抵抗を二次側につなぐと1200[V]の電圧が出る事になりますが、抵抗を接続しないで二次側を開放してしまったら一体何がどうなってしまうのか考えます。
次の様な問題を考えます。
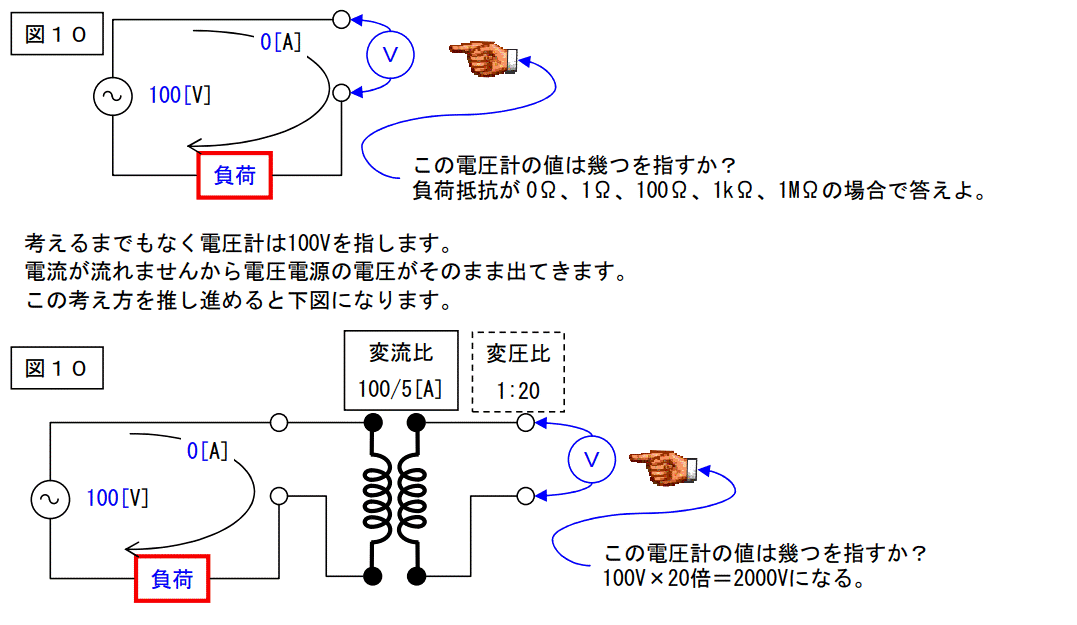
変流比が20:1の変流器は変圧比が1:20の変圧器でもあります。
一次側に100Vの電圧電源が接続されれば二次側は自動的にその20倍の2000Vになります。
つまりこの理論で考えれば、CTの二次側を開放すれば電源電圧の1/変流比倍(=変圧比倍)の電圧が二次側端子に出ます。
今回の場合は2000[V]が理論上の最高電圧で、これ以上の電圧は出ません。
変圧器の二次側を開放すると一次側に電流は流れません。(励磁回路は考えない、と言う考え方です。)
何やら変な結論が出ていますが、もう少し我慢して次の問題を考えてください。
今度は電源電圧を6600Vにした場合の話です。
負荷容量は負荷電流が60Aになるように調整してあります。
CTの二次側が「短絡」「負荷抵抗が1kΩ」「開放」の場合を各々考えてください。
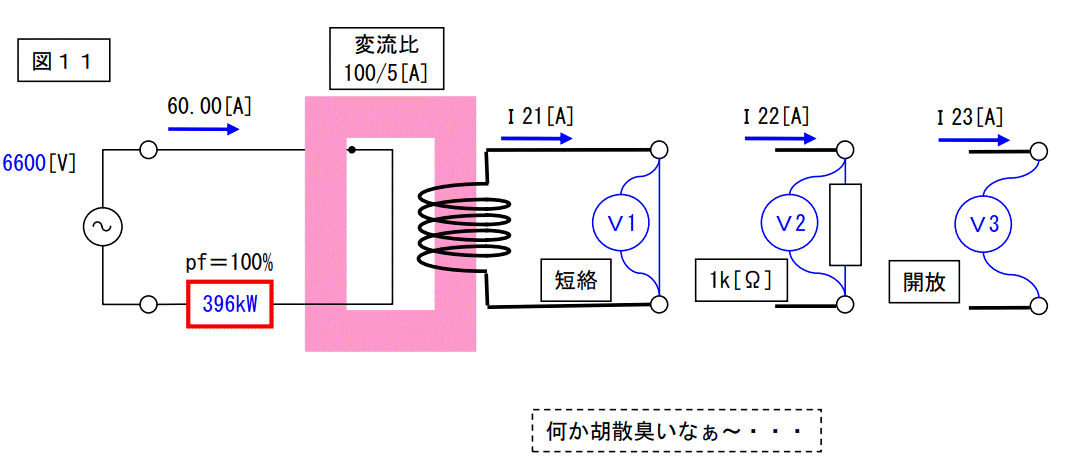
電圧電源が 100V の場合と同様に計算を進めます。
短絡した場合は電圧が出ませんので V1=0[V]です。
6600V396kW 抵抗負荷の抵抗値は 110[Ω]です。
CT の二次側に 1[kΩ]の抵抗を接続した場合の CT 一次側への換算抵抗値は電源電圧に関係なく 2.5[Ω]になります。
電圧電源の 6600V を 110Ωと 2.5Ωの案分で分圧することになり 2.5Ωの分圧は次の式になります。
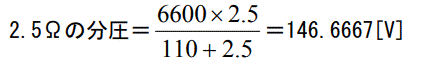
CT の二次側にはこの 20 倍の電圧が出ますので V2=146.6667×20=2933[V]の電圧になります。
開放した場合は電源電圧がそのまま出ますので V3=6600×20=132[kV]!となります。
電流値はI21 は 60A の 1/20 で 3[A]です。
I22 はI22={6600/(110+2.5)}/20=2.9333[A]となり 3]A]と大きく変わりません。
I23 はゼロ[A]です。
同じ 60[A]でも 100V の場合と随分結果が違います。
もう少し例題を考えてみましょう。今度は電圧を 24[V]にした場合です。
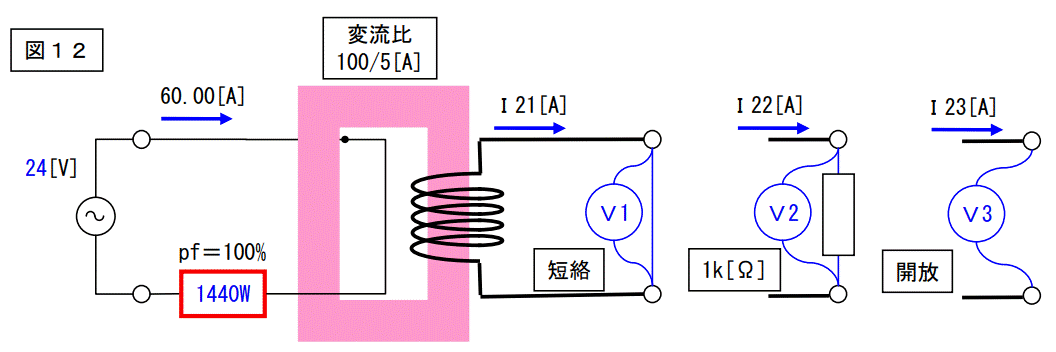
計算手法は同じですから経過は省略して結果だけを書きます。
1440[W]の抵抗値=24[V]÷60[A]=0.4[Ω]
V1=0[V]、I21=3[A]
V2=414[V]、I22=0.41[A]
V3=480[V]、I23=0[A]
この様に同じ 60[A]を変流する変流器でも一次側の電源電圧や負荷の具合によって相当に異なる挙動になる事が解ります。
つまり、電流値が同じでも一次側の扱っている電圧が高くなればなるほど二次端子に高い抵抗値を接続したり開放した場合に出てくる電圧は高くなります。
取り敢えず3つの電圧で考えて視ましたが、下記のような事が言えると思います。
CTの挙動に関して電流が同じで有れば電圧は関係ないとは言えない。
当たり前の話ですが、此処まではCTを理想変成器として扱った結果です。
このままでもう少し解析します。
少し整理しましょう。
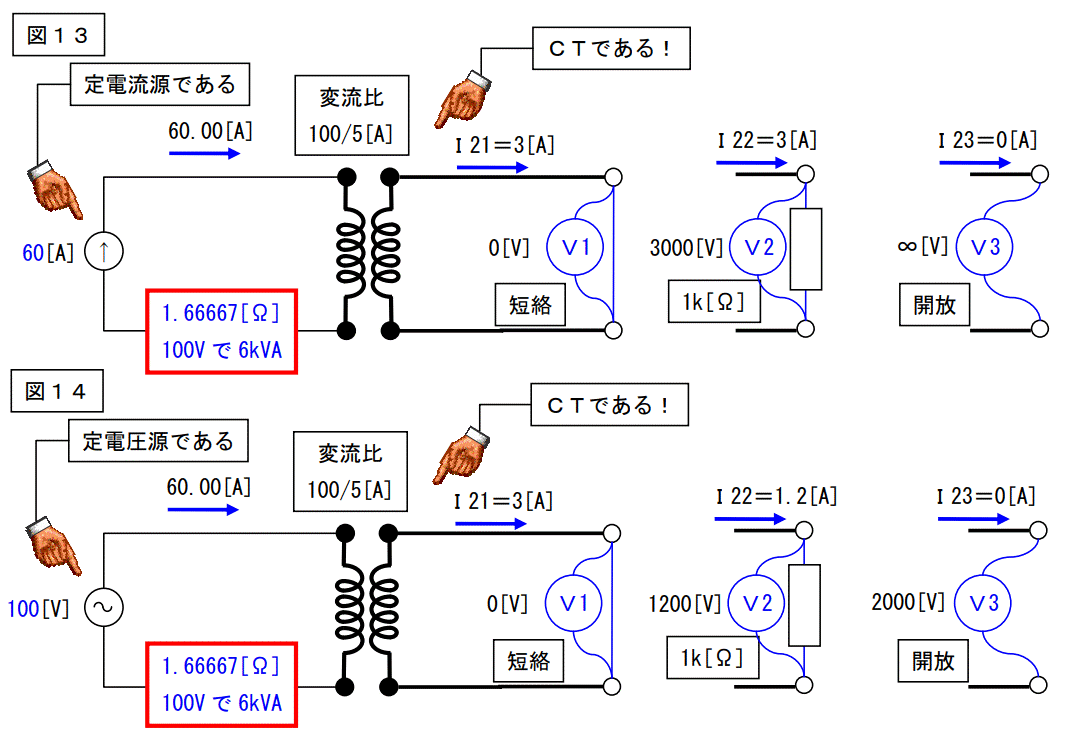
図13は当初の考え方を書いたものです。
CTの一次側の回路はCTとは関係なく独立している回路と考えました。
一次側は「定電流電源の回路」と見なして解析を行いました。
結果として二次側に 1kΩの抵抗を並列すれば 3000V の電圧が発生し、開放すれば無限大の電圧になります。
今回の考え方はこの考え方をもう少し現実的に考えて解析し直したものです。
図14に示すようにCTの一次側と二次側は変成器である変流器CTに依って結合されているので、二次側の回路に依って一次側も変化するという考え方です。
結果として 1kΩを接続すると 1200V の電圧が発生し、開放すると 2000V になります。
つまりこの理論での最高電圧は 2000V で、3000V にはなりません。
電源電圧が 24V の時は 480V で済みますが、6600V の時は 132kV と言う恐ろしい数値になる事は前述の通りです。
此処で最初の話に戻って考えます。
下図は二次側に 1[kΩ]の抵抗を接続した場合のもので同じものを書いていますが、図 16 に示すV1 の電圧=60[V]は図 15 の何処に出ているのでしょうか?
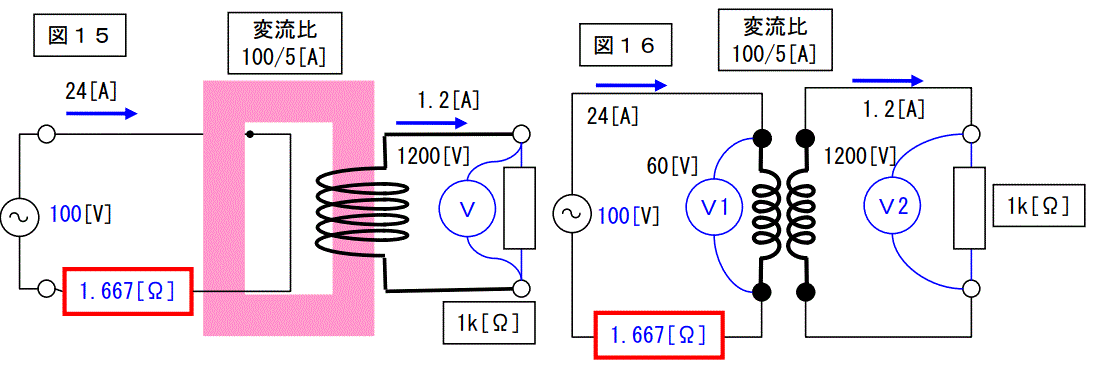
この計りようのない電圧を計る事を考えます。
先ず下記の回路を見てください。
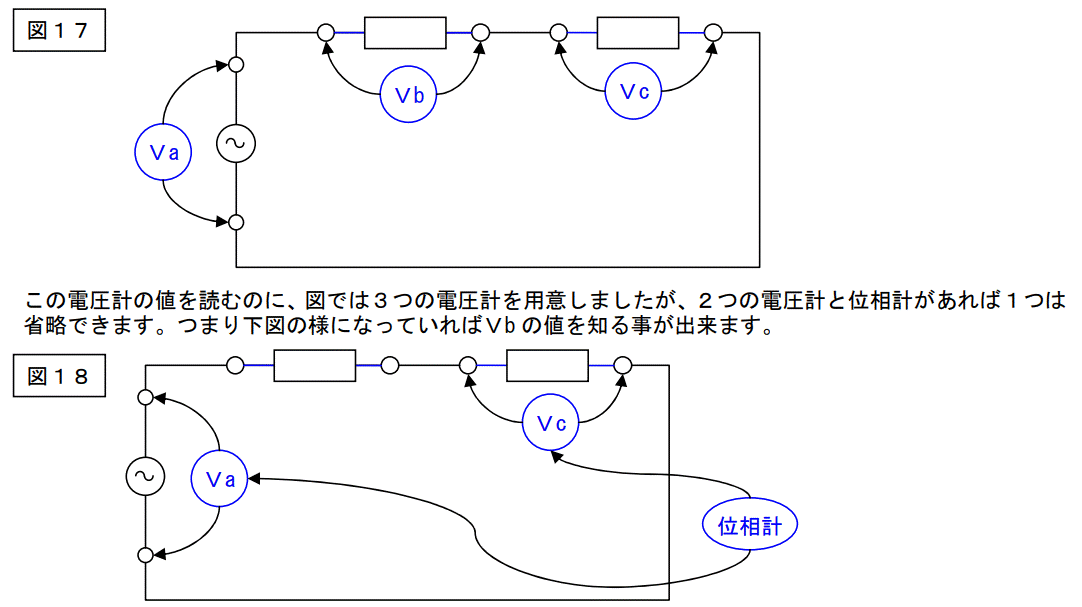
これと同様の事を図15に適用すれば図16のV1 に該当する電圧を計算で求める事が出来ます。
つまり下図のように電圧計を置いて、電圧を測ると共に電源電圧との位相を計ればベクトル演算で図16におけるV1 に該当する電圧を求める事が出来ます。
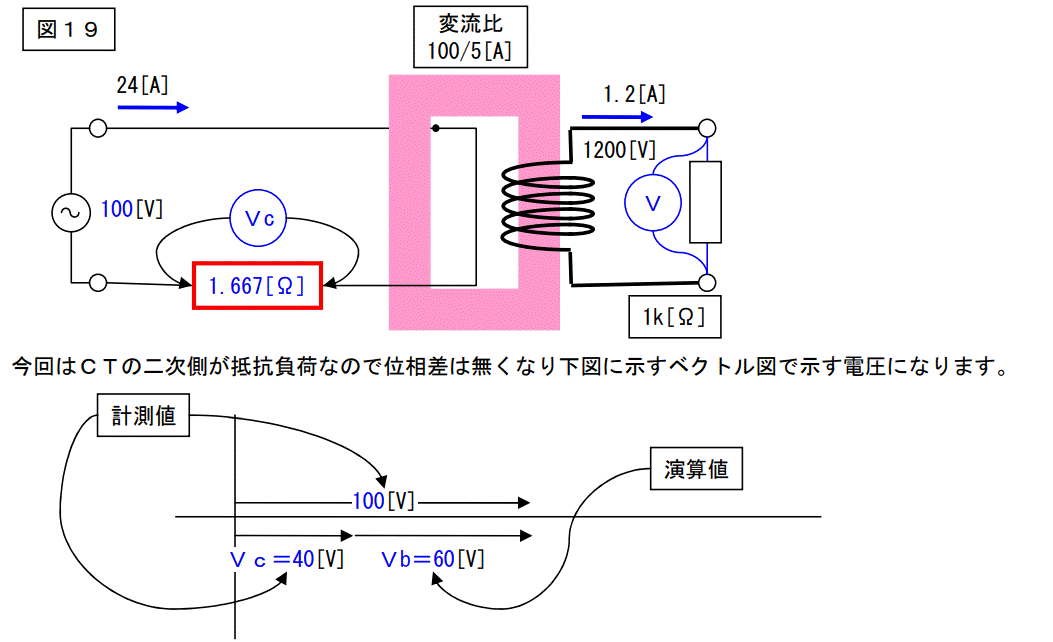
これで行方不明になっていた電圧を捕捉する事ができました。
意外なところに電圧が隠れていました。
次回はCTの負担(容量)と磁気飽和の事を書きます。
Coming soon Coming soon
コメント